стат / Задача 1

Задача 1. Система состоит из N >> 1 независимых частиц, каждая из которых может находиться в одном из двух квантовых состояний с энергиями – и . Определить энтропию S состояния с энергией Определить температуру Т этого состояния. Вычислить энтропию при Т = 0. Найти равновесное число частиц в верхнем состоянии, а также равновесную энергию и теплоемкость как функции температуры Т.

Решение. Пусть - число частиц на нижнем уровне двухуровневой системы, а - число частиц на верхнем уровне, так что Энергия всей системы тогда равна Следовательно, Такое состояние можно достичь

(1)

способами (число сочетаний). Это – статистический вес состояния с энергией Е. Энтропия системы равна логарифму статистического веса (числа состояний): Согласно формуле Стирлинга для больших чисел

(2)

Пренебрегая фактором , получим для энтропии

. (3)

Статистическая температура определяется соотношением

(4)

Подставляя (3) в (4), находим:

(5)

Должно быть Т > 0 (нормальная система): в противном случае статистическая сумма обратится в бесконечность. Следовательно, согласно (5) должно быть n < 0. Если , то согласно (5) При этом все частицы находятся на нижнем уровне (одно квантовое состояние). Согласно (3) при этом энтропия стремится к нулю (теорема Нернста). Далее, из (5) находим равновесное число частиц на верхнем уровне

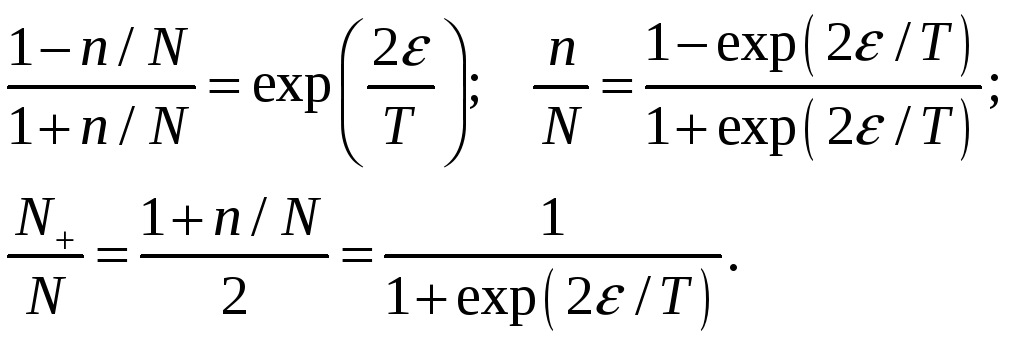(6)

Этот же результат можно получить независимо и из распределения Гиббса Рассмотрим одну частицу, которая может находиться на нижнем или на верхнем уровнях. В данном случае энергия квантового состояния для верхнего уровня , а нормировочный множитель .

Из (6) далее определяем энергию при заданной температуре Т:

(7)

Наконец, из (7) находим теплоемкость:

(8)

На рис. 1 представлен согласно (7) график в зависимости от величины . При большой температуре эта энергия стремится к нулю (равнозаселенность уровней). Напротив, при нулевой температуре энергия равна (все частицы на нижнем уровне).

>

Рис. 1.

На рис. 2 представлен график C/N в зависимости от величины . Видно, что теплоемкость (так называемая теплоемкость Шоттки) содержит резкий (и неочевидный) максимум при значении вблизи единицы.

>

_{Рис. 2.}