стат / Задача 20

Задача 20. Найти распределение частиц по импульсам и спектр квазичастиц для основного состояния слабонеидеального бозе-газа с отталкиванием при нулевой температуре.

Решение. Гамильтониан системы парно взаимодействующих бесспиновых бозонов в представлении вторичного квантования имеет вид

, (1)

причем согласно закону сохранения импульса . Для слабого взаимодействия лишь малая доля частиц из полного числа частиц N выходит из бозе-конденсата. Следовательно, импульсы частиц вне бозе-конденсата малы. Их волновые функции представляют собой плоские волны; при малых импульсах они имеют простой вид (V – объем системы). Следовательно, матричный элемент взаимодействия можно записать в виде

Для частиц внутри конденсата число частиц равно

Поэтому соответствующие операторы можно заменить на числа:

Упростим взаимодействие с учетом указанных соображений:

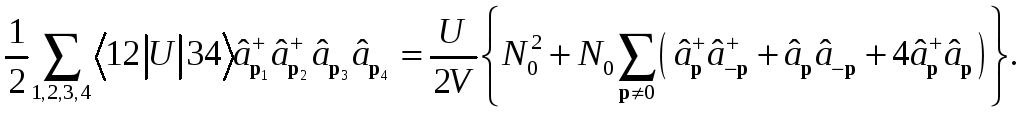(2)

Фактор 4 возник из-за четырех возможных перестановок операторов в левой части этого выражения. Приведенные значения импульсов учитывают закон сохранения импульса. Пренебрегаем также слагаемыми во взаимодействии с меньшими степенями числа частиц

Аналогичным образом упрощаем выражение для числа частиц

откуда

Подставляя это соотношение в первое слагаемое правой части (2), получим взаимодействие в виде

.

Введем обозначение

(величина u имеет размерность скорости). Окончательное упрощенное выражение для гамильтониана приобретает вид

. (3)

(слагаемые, не зависящие от операторов, включены в ).

Чтобы перейти от системы взаимодействующих частиц к системе независимых квазичастиц, произведем преобразование Боголюбова к новым операторам рождения и уничтожения квазичастиц

(4)

Как операторы частиц, так и операторы квазичастиц должны удовлетворять правилам коммутации бозе-операторов

.

Первое правило удовлетворяется по определению. Легко проверить, что второе правило выполняется, если Следовательно, преобразование (4) можно переписать в виде

(5)

Подставим (5) в (3) и потребуем, чтобы коэффициент при был бы равен нулю (тогда автоматически будет равен нулю и коэффициент при ). Получаем уравнение для

. (6)

Здесь введена безразмерная величина, характеризующая интенсивность взаимодействия

.

Решение квадратного уравнения (6) имеет вид

(7)

(другое решение не обращается в нуль при выключении взаимодействия, u = 0). Подставляя (5) в (3), получим гамильтониан невзаимодействующих квазичастиц

(8)

(слагаемые, не зависящие от операторов, включены в ).

Подставляя (7) в (8), получим спектр энергий квазичастиц

(9)

При взаимодействием можно пренебречь и Напротив, при получаем фононный спектр

Число частиц вне бозе-конденсата дается соотношением

Подставляя (5) в это соотношение и учитывая, что для квазичастиц при нулевой температуре , получим

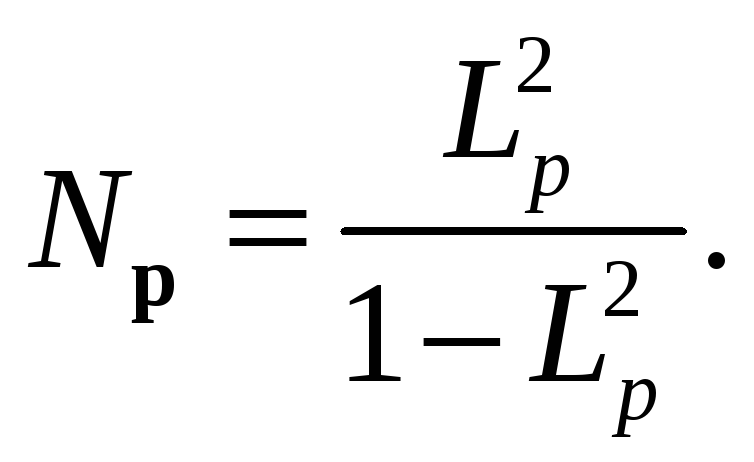
Подставляя (7) в это выражение, находим распределение частиц по импульсам вне бозе-конденсата

(10)

В частности, при отсюда находим Напротив, при получаем Число частиц в конденсате равно

Подставляя (10) в это соотношение и вычисляя элементарный интеграл, находим число частиц в бозе-конденсате

. (11)