стат / Задача 5

Задача 5. Определить разность теплоемкостей в переменных а) V,T; б) P,T. Определить для а)идеального больцмановского газа: б) газа Ван-дер-Ваальса; в) идеального вырожденного ферми-газа при ; г) фотонного газа.

Решение. По определению

Итак,

(1)

Упрощаем правую часть этого соотношения, используя выражение для дифференциала свободной энергии . Следовательно,

(2)

Подставляя это соотношение в (1), окончательно находим

(3)

Теперь рассмотрим примеры.

а) уравнение Клапейрона для идеального газа имеет вид Следовательно,

Подставляя эти соотношения в (3), находим простое хорошо известное соотношение

(4)

б) уравнение Ван-дер-Ваальса имеет вид

Следовательно,

Подставляя эти соотношения в (3), находим

(5)

Отметим, что при а = 0 отсюда получим снова соотношение (3) для идеального газа, хотя b может быть отлично от нуля.

в) перепишем (3) с учетом (2) в виде

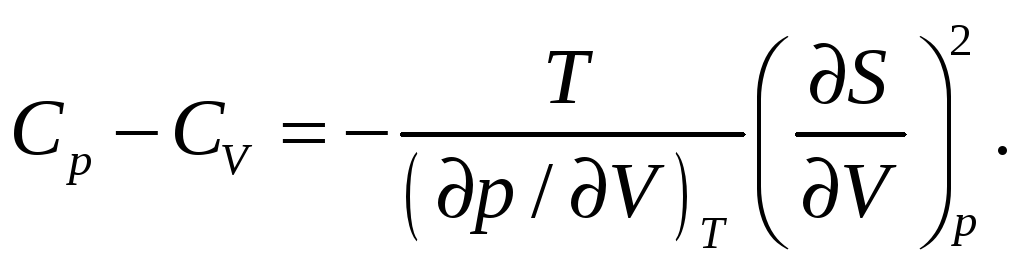(6)

Энтропия газа Ферми при равна

Уравнение состояния газа Ферми при имеет вид

Подставляя эти соотношения в (6), находим малое отличие между теплоемкостями, кубичное по температуре:

(7)

г) фотонный газ (черное излучение). Уравнение состояния имеет вид

Так как , а конечно, то согласно (3) имеем При этом теплоемкость является конечной, а - бесконечной величиной.

д) повторяем рассуждения раздела а) с заменой давления на объем и наоборот:

Итак,

(8)

Для термодинамического потенциала имеем Следовательно,

Подставляя это соотношение в (8), окончательно находим

(9)