стат / Задача 19

Задача 19. Для идеального равновесного ферми-газа вычислить коррелятор флуктуации плотности при низких температурах по сравнению с энергией Ферми. Здесь - флуктуация плотности числа частиц в точках .

Решение. Оператор числа частиц имеет вид

(1)

Для краткости здесь мы не пишем здесь спины частиц. Волновые функции частиц представляют собой плоские волны

Диагональные элементы суммы (1) при усреднении по равновесному распределению представляют собой хорошо известную среднюю плотность ферми-частиц

Таким образом, флуктуацию плотности можно записать в виде

. (2)

Здесь штрих у суммы означает, что из нее следует выбросить диагональные элементы.

Для вычисления коррелятора флуктуации плотности перемножаем два выражения типа (2), относящиеся соответственно к координатам . Вследствие закона сохранения импульса из всевозможных произведений отличны от нуля только слагаемые, в которых имеется две пары операторов с одинаковыми индексами, т.е. слагаемые вида

.

При статистическом усреднении по равновесному распределению ферми-частиц в этом выражении можно заменить

.

Тогда эта сумма приобретает вид

Подставляя в нее приведенные выше волновые функции частиц, перепишем ее в виде

. (3)

Заменяем здесь сумму по импульсам на интеграл. При этом возникает два слагаемых . В первом слагаемом имеем

Множитель 2 в числе состояний отражает две проекции спина ½ ферми-частицы (операторы не содержат зависящих от спина членов, поэтому проекции спинов обеих частиц одинаковы, т.е. в числе состояний надо писать фактор 2, а не 4). Интегрирование по дает дельта-функцию . Следовательно, первое слагаемое приводит к тривиальному результату, не связанному с корреляциями:

По определению имеем

.

Таким образом, именно второе слагаемое в (3) определяет корреляционную функцию

или

(4)

Интегрируем в (4) по углам вектора импульса р и подставляем функцию распределения Ферми. Получаем

(5)

Рассмотрим предел нулевой температуры, когда функция распределения представляет собой ступенчатую функцию Хевисайда. Из (5) находим

Вычисляя элементарный интеграл, находим для коррелятора осциллирующую функцию

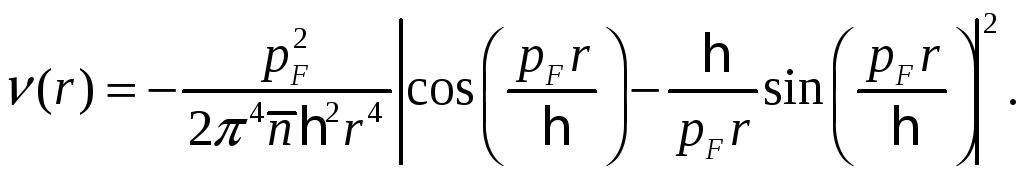
Подставляя , получим

(6)

Условие применимости состоит в том, чтобы флуктуации величины были бы малы по сравнению с самой величиной. Таким образом, должно быть . Подставляя (6), находим Следовательно, вторым слагаемым в (6) мы должны пренебречь по сравнению с первым. Получаем окончательно быстро осциллирующую функцию (осцилляции Фриделя)

(7)

Усредняя по осцилляциям, получим среднее значение флуктуаций плотности ферми-частиц при нулевой температуре

(8)

Теперь обратимся к случаю низких, но ненулевых температур (температура мала по сравнению с энергией Ферми). Согласно (5) имеем

Перепишем интеграл J в виде

. (9)

Интегрируя по частям, находим

Произведем замену переменной интегрирования

Последнее упрощение связано с тем, что малых температурах существенно интегрирование только вблизи значений энергии, близких к энергии Ферми. По этой же причине интегрирование по x можно распространить на весь интервал Получаем

В подынтегральном выражении можно заменить

так как второе слагаемое обратит интеграл в нуль из-за нечетности подынтегрального выражения по x. Обозначая далее

,

перепишем указанный интеграл в виде

Из справочника интегралов имеем

В данном случае Таким образом, получаем

Подставляя это выражение в (9), находим

(10)

В условиях низких температур должно быть Поэтому в (10) надо дифференцировать только числитель. Получаем

Следовательно,

Подставляя , получим окончательно

(11)

При отсюда получим выражение (7), как и должно быть. Напротив, при повышении температуры экспоненциальный рост знаменателя в (11) превышает степенной рост числителя, так что коррелятор флуктуации плотности уменьшается и становится экспоненциально малым. Однако экспоненциальная малость достигается при очень больших значениях расстояния между ферми-частицами r:

Усредняя (11) по осцилляциям Фриделя, получим

(12)