стат / Задача 25

Задача 25. Найти обменную энергию электронной плазмы при нулевой температуре.

Решение. Кулоновская энергия взаимодействия между двумя электронами плазмы равна

Оператор этого взаимодействия между электронами в представлении вторичного квантования равен

. (1)

Здесь

(2)

- волновые функции свободных электронов, V – объем системы.

Энергия системы в первом порядке теории возмущений равна диагональному матричному элементу оператора (1). При этом оператор прямого взаимодействия соответствует условиям , а оператор обменного взаимодействия условиям

. Импульсы мы будем считать отличными друг от друга, так как если все импульсы одинаковы, то число таких состояний ничтожно мало по сравнению с числом состояний с различными импульсами, так что первыми можно пренебречь. Для оператора обменного взаимодействия вследствие правил коммутации операторов Ферми с разными импульсами имеем

.

При усреднении по вакуумному состоянию получим, что эта величина равна произведению чисел заполнения состояний . Подставляя это произведение и (2) в (1), находим энергию обменного взаимодействия

(3)

Входящий сюда интеграл вычисляется заменой переменной . Получим (фактически вычисляем фурье-компоненту от кулоновского потенциала)

Подставляя это выражение в (3), находим

Далее заменяем сумму по импульсам на интеграл с учетом квазиклассического числа состояний (дополнительный фактор 2 отражает два значения спина в числе состояний)

(4)

Отметим, что число спиновых состояний равно 2, а не 4, так как кулоновское взаимодействие не меняет спина частицы.

Вычисляем интеграл, входящий в выражение (4):

(5)

имея в виду, что при нулевой температуре числа заполнения являются ступенчатыми функциями Хевисайда. Следовательно, в (5) произведение равно единице, только когда и . В остальных случаях оно равно нулю. Здесь импульс Ферми определяется соотношением (см. предыдущие задачи)

Заменим переменные интегрирования на переданный (q) и удвоенный суммарный (P) импульс

Якобиан такого преобразования равен единице. Следовательно,

. (6)

Вычисляем сначала интеграл при фиксированном значении q

При условии этот интеграл есть объем шара радиуса , который сдвинут влево от начала координат на q/2. При условии этот интеграл есть объем шара радиуса , который сдвинут вправо от начала координат на q/2. При выполнении обоих условий этот интеграл есть объем, заключенный между двумя шарами радиуса каждый, причем центры шаров раздвинуты друг от друга на расстояние q. Половина этого объема представляет собой область, заштрихованную на рис. 1.

Рис. 1

Величина этого объема равна

.

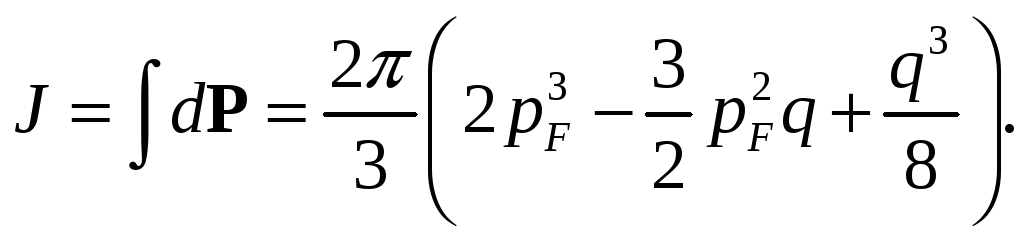Подставляя это выражение в (6), получим

Из (4) находим обменную энергию

(7)