стат / Задача 22

Задача 22. Используя уравнения Боголюбова де Жена, определить коэффициенты в функционале Гинзбурга-Ландау через микроскопические параметры гамильтониана.

Решение. В предыдущей задаче 21 было получено уравнение (21) для щели в энергетическом спектре сверхпроводящего ферми-газа

(1)

Коэффициенты преобразования Боголюбова даются соотношением (22) из задачи 21 (в отсутствие сверхпроводящего тока, т.е. q = 0)

Для этих коэффициентов было получено уравнение (23) в задаче 21

(2)

Здесь Далее, - функция распределения Ферми для свободных квазичастиц.

Так как операторы квазичастиц должны удовлетворять правилам антикоммутации, как и операторы ферми-частиц, то из соотношения (11) задачи 21 следует, что . Из (2) тогда следует явный вид коэффициентов преобразования Боголюбова

Подставляя эти значения в (1), находим уравнение для определения величины :

(3)

Пределы интегрирования по здесь распространены в обе стороны от , так как в интеграле существенна лишь область импульсов электронов вблизи импульса Ферми. Следует отметить, что в металле пределы интегрирования распространяются не до энергии Ферми, а до температуры Дебая (которая мала по сравнению с энергией Ферми), так как электроны взаимодействуют друг с другом, обмениваясь фононами кристаллической решетки. Это взаимодействие эффективно, пока энергии электронов не превышают существенно энергии фононов.

При нулевой температуре из (3) получим уравнение

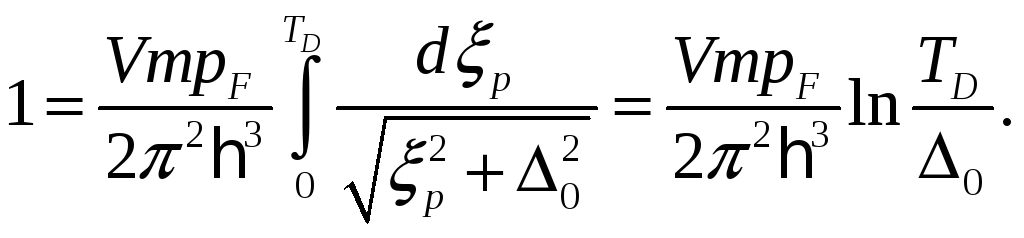(4)

Отсюда

(5)

Обратимся теперь к общему случаю конечных температур. Запишем уравнение (3) в виде

Здесь было использовано соотношение (4) с заменой . Подставляя в левую часть этого уравнения выражение (4), перепишем его в более простом виде

. (6)

Ввиду сходимости интеграла верхний предел в (6) распространен до бесконечности.

Теперь обратимся к окрестности точки фазового перехода, где величина мала. Заменим переменную интегрирования в (6) и обозначим . Далее, перепишем интеграл в правой части (6) в виде

(7)

Вычислим отдельные части этого интеграла

. (8)

Далее,

(9)

(интеграл вычислялся на компьютере). Итак,

(10)

(константа С сокращается). В двух последних слагаемых интеграла в (7) проводим разложение в ряд Тейлора

(11)

(интеграл также вычислялся на компьютере). Подставляя (10) и (11) в (6), Находим

(12)

Из (12) следует, что щель обращается в нуль при критической температуре

(13)

В окрестности критической температуры из (12) имеем

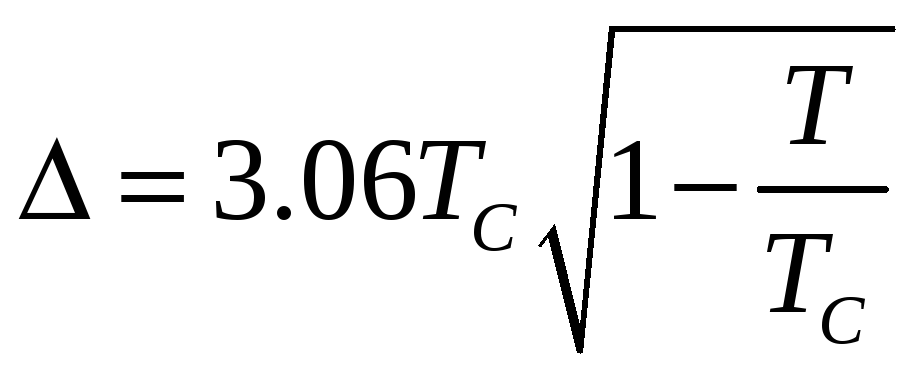(14)

Для функционала Гинзбурга-Ландау (свободная энергия), отнесенного к единице объема, в окрестности критической точки можно написать (задача 16)

Величина определяется из минимума потенциала:

Подставляя в это соотношение выражение (14), находим и

. (15)

Итак, равновесное значение свободной энергии равно

(16)

С другой стороны, эту величину можно вычислить, исходя из микроскопического гамильтониана. Воспользуемся формулой квантовой механики

(17)

где  - параметр задачи. В данном случае в качестве этого параметра выступает амплитуда взаимодействия V. Отметим также, что в действительности здесь в качестве термодинамического потенциала выступает не свободная энергия, определенная при заданном числе частиц, а, как мы видели в задаче 21, термодинамический потенциал , определенный при заданном химическом потенциале, т.е. фиксированной энергии Ферми.

Дельта-функционное взаимодействие между электронами, приводящее к спариванию электронов с противоположными импульсами и спинами, обсуждалось ранее (формула (5) в задаче 21). В представлении вторичного квантования, это взаимодействие, выраженное через операторы рождения и уничтожения частиц, записывается в виде (оно отнесено к единице объема)

Произведем преобразование Боголюбова для перехода к операторам квазичастиц

Тогда взаимодействие приобретает вид

(18)

где

При усреднении этого выражения при заданных числах заполнения квазичастиц первые два слагаемых исчезают, а из последнего слагаемого получим (такая операция уже проводилась в задаче 21 при получении уравнения для )

Следовательно, из (18) получим, учитывая (1)

(19)

Согласно (17) и (18) находим

(20)

Дифференцируем соотношение (12):

(21)

Из (5) следует, что

(22)

Подставляя (22) в (21), находим

(23)

Подставляя далее (23) в (20), вычисляем интеграл

(24)

Подставляя (14) в (24), находим окончательное микроскопическое выражение для свободной энергии, связанной со спариванием электронов:

(25)

Сравнивая микроскопическое выражение (25) с феноменологическим выражением (16), находим

(26)

(здесь мы воспроизвели также и соотношение (15)). Из (26) находим значение а:

(27)

Можно ввести энергетическую плотность состояний при нулевой температуре

Здесь

- число электронов в единице объема с заданной проекцией спина. Тогда окончательные выражения для феноменологических коэффициентов в функционале Гинзбурга-Ландау через параметры микроскопического гамильтониана приобретают вид

(28)