стат / Задача 6

Задача 6. Найти колебательную и вращательную теплоемкости двухатомных молекул, составленных из разных атомов. Исследовать случаи высоких и низких температур.

Решение. Начнем с вращения двухатомных молекул. Энергия вращения имеет вид

Здесь I – момент инерции молекулы, K – вращательное квантовое число. Вращательные уровни вырождены (2K + 1) раз. Вращательная статистическая сумма для одной молекулы имеет вид

(1)

Аналитически она не вычисляется. Для N молекул вращательная статистическая сумма имеет вид Соответствующая свободная энергия равна

Обычная энергия Е определяется как Получаем (для одной молекулы) для энергии и вращательной теплоемкости:

(2)

График вращательной теплоемкости показан на рис. 1 в зависимости от безразмерного параметра

Рис. 1.

Видно, что вращательная теплоемкость на определенном участке превышает единицу, но стремится к ней при высоких температурах.

Аналитически можно найти теплоемкость при низких и высоких температурах. При низких температурах, когда , оставляем в статистической сумме только два слагаемых В том же приближении свободная энергия равна 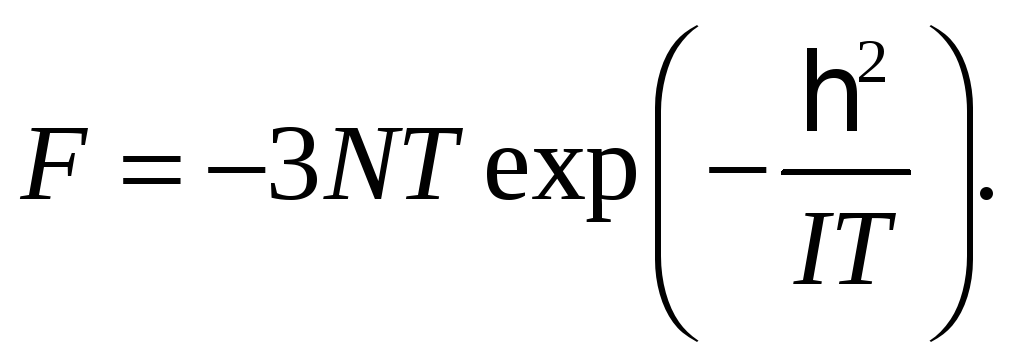Вращательная теплоемкость )в расчете на одну молекулу) получается равной

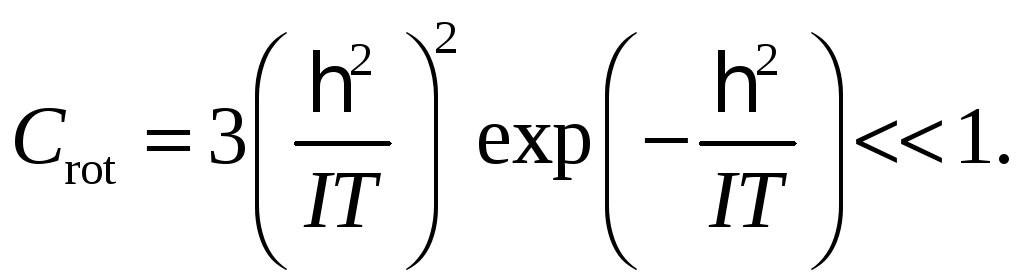(3)

В случае высоких температур, когда , для вычисления статистической суммы используем формулу Эйлера-Маклорена

В применении к (1) получим (сохраняя члены 1/x << 1)

Следовательно, свободная энергия имеет вид

Обычная энергия равна

Окончательно для вращательной теплоемкости получим (в расчете на одну молекулу)

(4)

Отсюда следует, что она стремится к единице сверху, как это видно из рис. 1.

Теперь обратимся к колебательной части теплоемкости. Квантовая энергия гармонических колебаний имеет вид

Колебательная статистическая сумма вычисляется элементарно (для одной молекулы)

Свободная энергия равна (для N молекул)

.

Обычная энергия равна

Для колебательной теплоемкости находим (в расчете на одну молекулу)

(5)

Ее график как функция безразмерного параметра представлен на рис. 2.

Рис. 2.

При низких температурах теплоемкость согласно (5) экспоненциально мала

Напротив, при высоких температурах согласно (5) она стремится снизу к единице по закону

.