3. Основы механики и термодинамики многофазной и многокомпонентной фильтрации

Вводные замечания.Существуют различные точки зрения на характер естественных флюидных процессов в баженовской свите. Допустимы также разные технологии воздействия. Поэтому разумно сначала привести общую схему подземной гидрогазодинамики, которая охватывает все принятые к рассмотрению геологические модели баженовской свиты и все технологии ее разработки. Она сводится к механике и термодинамике термопороупругости с многофазным и многокомпонентным флюидом [5,6,7]. Для простоты и определенности изложения будем считать, что пористая среда является однородной и изотропной. В численных моделях эти ограничения не являются существенными и легко снимаются. В общей постановке учитываются процессы пороупругости и разрушения, хотя в основной модели ими или пренебрегается или они учитываются косвенным образом. Тем не менее, мы сочли целесообразным привести самую общую постановку. Дело в том, что в процессе уточнения и исследований технологий в каких-то случаях могут оказаться востребованными быстрые изменения режима, при которых упругими деформациями скелета уже нельзя будет пренебречь. Общая постановка позволяет без труда включить эти процессы в заданную схему.

Ограничимся квазистационарными (т.е. безынерционными) неизотермическими процессами. Жидкая смесь в поровом пространстве представляет собой систему из фаз (каждая из которых фильтруется со своим коэффициентом фазовой проницаемости) икомпонентов. Скелет также состоит из нескольких фаз, которые в процессе термогазового воздействия меняют свою насыщенность. В общем случае в результате воздействия меняются и параметры трещиноватости скелета. Упругие смещения и деформации скелета будем считать малыми, а все определяющие соотношения – линейными по обобщенным силам и потокам. Вязкие и пластические деформации скелета малыми не являются.

В общем случае система является многофазной и многокомпонентной. Состав фаз и компонентов определяется свойствами баженовских пород, а также выбором той или иной технологии воздействия. Средние значения величин, относящихся к флюидным фазам будем обозначать верхними латинскими символами () и (). Компоненты будем отмечать нижними греческими символами. Скелетную фазу будем обозначать верхним индексом (s). Величины, относящиеся ко всему элементарному объему, будем оставлять совсем без индексов.

Твердую фазу керогена разумно включить в состав скелета, а флюидные фазы считаются подвижными и могут фильтроваться. Таким образом, мы приходим к задаче с однофазным скелетом и флюидом, допускающим физико-химические превращения с участием скелетной фазы. Многие конкретные расчеты в целях простоты проводятся для частного случая только двух флюидных фаз (жидкой и газовой). В этом случае индекс относится к жидкости, а индекс– к газу. При тепловом и химическом воздействии возможен переход твердой фазы в жидкую и газовую фазы. В модели с двойной пористостью чисто формально поры и трещины рассматриваются как разные фазы с числовыми индексами 1 и 2.

Пусть – полная пористость среды. Аналогом пористости для каждой фазы являются объемные доли флюидных фаз, которые называются фазовой (или парциальной) пористостью. Они связаны с насыщенностьюсоотношением. Пусть,,– плотности двухфазной среды, скелетной и флюидных фаз, а,удельная внутренняя энергия двухфазной среды, упругой и жидкой фаз. Каждая фаза может состоять из компонент. Компоненты характеризуется приведенной плотностьюи массовой концентрацией, которые также связаны между собой. Из определения экстенсивных величин вытекают следующие соотношения аддитивности

,,,,

,,, (3.1)

,,. Здесь,– тензоры полных напряжений в элементарном объеме и напряжений, осредненных по объему скелета,– поровые давления фаз,– единичный тензор.

К кинематическим величинам относятся истинные скорости флюидных фаз и фазовые (парциальные) скорости фильтрации. Скорость(и смещение) элементарного объема пористой среды отождествляется со средней скоростью скелета по скелетной фазе:(). Скоростьотличается от скороститем, что последняя не определена в порах, в которых величиныидоопределяются по непрерывности.

Уравнения пороупругости. Простейшим вариантом пороупругой модели является модель Био [8]. Уравнения Айфантиса [9] обобщают уравнения Био. Частным случаем, вытекающим из уравнений Айфантиса, является модель с двойной пористостью Баренблатта. Мы рассматриваем модель пороупругой среды Айфантиса с учетом химических и физико-химических превращений и рассеянного разрушения. В уравнениях Айфантиса и Баренблатта поровое и трещинное пространства можно рассматривать как вместилища разных фаз. Поэтому модель с двойной пористостью является частным случаем общих уравнений механики пористых деформируемых сред.

Уравнения пороупругости для пористых сред с многофазным флюидом можно разделить на две группы. Одна из них описывает динамику скелетной фазы

, а)

,b) (3.2)

,,. с)

Здесь – тензор эффективных (по Нуру) напряжений;– коэффициенты, введенные Айфантисом [8], которые аналогичны коэффициенту Био [8];– коэффициенты Ламе пороупругой среды, которые связаны с коэффициентом объемного сжатия соотношением;– объемное сжатие среды. Область определенияограничена внешней границей. Кроме того, она может содержать и внутренние границы. В системе координатосьнаправлена вертикальной вверх.

Вторую фильтрационную группу уравнений составляют соотношения баланса массы фаз и законы фильтрации. Каждая фаза может состоять из компонент. Для краткости в приведенных выражения скелет будем считать однофазным и однокомпонентным. Соответствующие обобщения реализуются очевидным образом. Компоненты характеризуется приведенной плотностью и массовой концентрацией. Для них имеем уравнения

. (3.3)

,, а)

,.b) (3.4) Здесь– скорость разложения керогена,– скорость фазовых превращений компонентаот фазык фазе().

Фильтрационные процессы описывает закон Маскета-Леверетта [7,10] для каждой фазы. В анизотропной среде вводятся тензор проницаемости . В общем случае в законе фильтрации необходимо учитывать также и перекрестные члены

,. Здесь– вязкость-той флюидной фазы.

Мы ограничимся случаем изотропной среды без перекрестных членов в законе фильтрации. Фазовая проницаемость может быть представлена в виде произведения абсолютной и относительнойпроницаемости

,,. (3.5)

В силу неравенств (5.2) – (5.4) упругими деформациями фаз, вообще говоря, можно пренебречь. Однако, если необратимые деформации отсутствуют, то тогда следует учитывать упругие деформации фаз. В этом случае необходимо учитывать уравнения состояния скелетной и флюидной фаз.

,,,

,. (3.6a) Здесь,объемные модули фаз, символозначает приращение данной величины. Для газа в общем случае имеем нелинейное уравнение состояния неидеального газа. В простейшем случае можно воспользоваться уравнением Клайперона-Менделеева

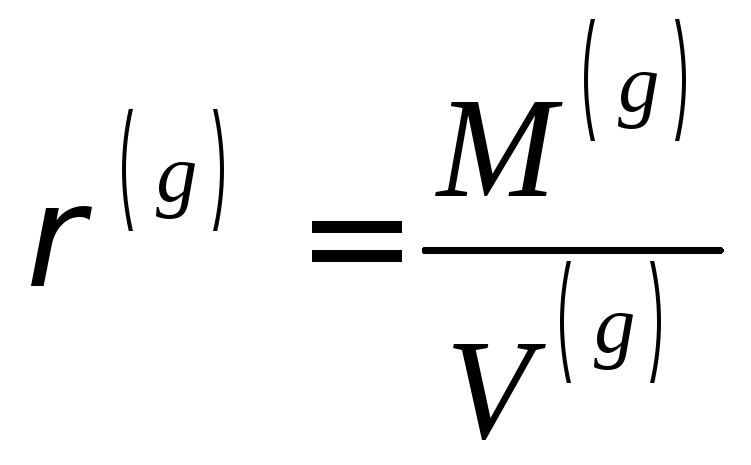,. (3.6b) Здесь,– объем и масса газовой фазы,– универсальный газовая постоянная,– температура.

Гомогенные химические реакции в i-той фазе между компонентами иподчиняются кинетическому закону. Поскольку кислород в нефти растворяется очень мало, то возможны и гетерогенные реакции, которые мы пока не конкретизируем. Реакции низкотемпературного окисления протекают в несколько стадий. В целях простоты мы ограничимся лишь простыми реакциями. В однородной и неподвижной среде кинетические соотношения принимают вид

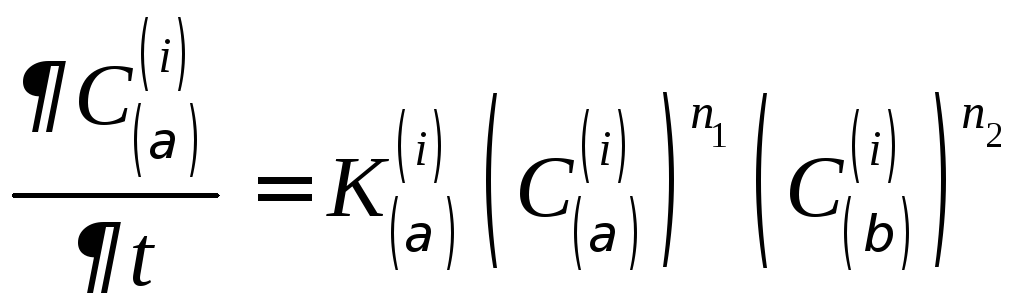. (3.7) Здесь– коэффициенты соответствующих химических реакций, которые зависит от температуры по закону Аррениуса. Описание сложных реакций с помощью (3.7) приводит к тому, что константы реакций в действительности зависят от концентраций. Следовательно, эта модель уже является достаточно грубой. Поэтому вполне допустимо дальнейшее упрощение модели при сохранении сути физических явлений.

Аналогичное кинетическое уравнение можно привести и для реакции разложения керогена. Пусть – относительная переменная доля (), которая уже подверглась превращению, а– максимальное значение пористости (оно порядка 4%). Тогда имеем

,при. а)

,.b) (3.8)

Приведем далее уравнения баланса энергии для всех фаз.

,a)

.b) (3.9) Здесь,– внутренняя энергия фаз,,– тепловые потоки фаз,,– температуры фаз,– упругий модуль вещества скелета,– коэффициент теплового расширения,,– энтальпии межфазовых превращений,– межфазные тепловые потоки,– тензор скорости деформаций,– градиент порового давления за вычетом гидростатической составляющей.

Каждая фаза находится в состоянии локального термодинамического равновесия, однако, фазы не находятся в равновесии друг с другом. Поэтому фазы имеют разную температуру, а между ними идут скалярные тепловые потоки. Балансовые соотношения дополняются кинетическими уравнениями теплопроводности для анизотропной среды

,a)

.b) (3.10) Здесь,– коэффициенты теплопроводности фаз.

Из (3.9), (3.10) после некоторых упрощений следует уравнение теплопроводности

,а)

.b) (3.11) Здесь– коэффициент теплопередачи между скелетной и флюидными фазами,,– удельные теплоемкости фаз,скрытая теплота преобразования керогена в жидкие и газообразные УВ,– скрытая теплота химических реакций (реакций низкотемпературного окисления), происходящих в к-ой флюидной фазе. Кроме того, коэффициенты компонент, участвующих в химических реакциях, связаны еще стехиометрическими соотношениями.

Коэффициент проницаемости в общем случае является функцией порового давления, первого и второго инварианта тензора деформаций и, а также пористости и температуры. Относительные фазовые проницаемости зависят только от насыщенности

,a)

,.b) (3.12)

Приведенные соотношения носят достаточно общий характер и рассчитаны на различные технологии воздействия. Для каждой из них необходимо конкретизировать структуру объекта, начальные и граничные условия, состав фаз и компонент, а также материальные константы и параметры воздействия. Дальнейшая конкретизация модели будет дана ниже.