4. Метод асимптотических разложений

Строгие методы осреднения были разработаны в первую очередь для регулярных сред с периодической микроструктурой. Здесь наиболее последовательно доказываются теоремы осреднения. Кроме того, для этих сред наиболее ясно и прозрачно проступает сама идея асимптотических разложений. Однако практически все геологические среды и протекающие в них процессы являются случайными. Поэтому в дальнейшем изложении существенное место занимает проблема осреднение в случайных пористых средах.

Рассмотрим проблему осреднение на простейшем примере плоского уравнения теплопроводности в периодической структуре

. (4.1) Здесь– температура,– коэффициент теплопроводности

На поверхности зерен выполняются естественные условия непрерывности температуры и теплового потока.

:,

,. (4.2)

На границе образца поддерживается нулевая температура

. (4.3)

Нашей целью является получение уравнений, которые не содержат быстро осциллирующих коэффициентов, но в каком-то смысле близки к истинным уравнениям. Ниже предлагается алгоритм такого решения.

Построение таких уравнений и их решение будем называть процедурой осреднения. Коэффициент теплопроводности в уравнении

. (4.4) с граничным условием (4.3) будем называть эффективным коэффициентом теплопроводности.

Для реализации этой процедуры перейдем к быстрым переменным по формулам

,.

При такой замене элементарная квадратная ячейка переходит квадрат, а уравнение (4.4) преобразуется в уравнение

. (4.5)

Рассмотрим вспомогательную задачу для функции , которая задается уравнением, определенным в открытом квадрате

(4.6) с граничными условиями на внутренней границе

:,,,

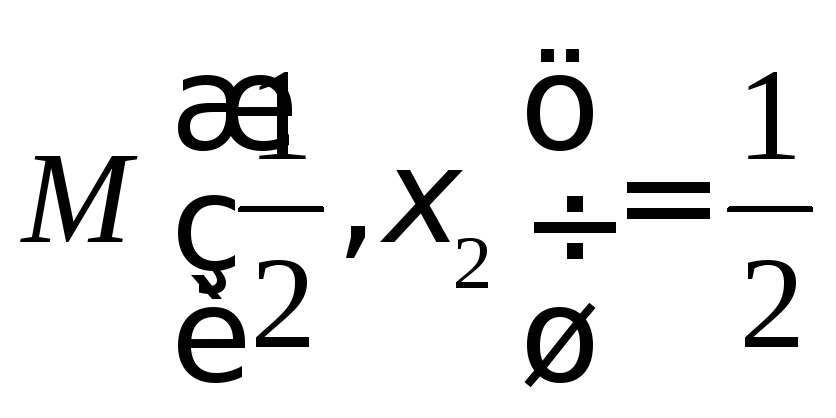,,,. (4.7)

Последняя задача решается численно. Доказано, что эффективный коэффициент теплопроводности имеет вид

. (4.8)

Оказывается, что указанная схема осреднения может быть формализована и приведена к некоторому простому виду с помощью некоторой процедуры асимптотического разложения. Заметим, что аргумент дважды входит в выражение для– как быстро осциллирующая и как медленно меняющаяся величина. Формально быстро и медленно меняющиеся аргументы можно рассматривать как независимые величины. В частности, можно произвести разложение по малому параметру

(4.9)

Оказывается, что нулевой член разложения температуры равен среднему значению данной величины. Точнее говоря, нулевой член разложения представляет собой решение задачи (4.4), (4.3). Асимптотический метод является универсальным. Доказаны теоремы о разрешимости задач, являющихся отдельными шагами в алгоритме построения асимптотического решения

5. Особенности механики жидких смесей

Как было показано выше, частицы жидких сред могут смещаться друг относительно друга на значительное расстояние, что при усреднении создает определенные трудности. Поэтому здесь нет законченной теории, и мы акцентируем внимание на некоторых моментах, с которыми связано определенное продвижение.

Отличительной чертой динамики жидких гетерогенных сред является тот факт, что существуют два принципиально разных режима движения – нестесненный и стесненный (т.н. "режим обтекания"). При анализе обоих режимов мы ограничимся простейшей ситуацией, в которой пренебрегается молекулярными силами взаимодействия частиц. Учет сил молекулярного происхождения значительно усложняет исследование, но при этом не меняет суть дела. Первый режим предполагает движение в бесконечном вязком пространстве, в котором находится конечное число частиц. В этом случае стенки сосуда не ограничивают движение частиц, и отсутствует дальнее воздействие частиц на другие частицы. В результате такого взаимодействия частицы стремятся занимать свободные места в вязком объеме и обеспечивая при этом минимум диссипации энергии. Характер движения частиц таков, что с точностью до малых величин высшего порядка возмущения скорости и давления от каждой частицы аддитивны, даже в пространстве между частицами. Этот факт подтверждается прямыми численными расчетами, экспериментами и сравнением с точными аналитическими решениями гидродинамических задач.

Совсем другая ситуация возникает в замкнутом сосуде конечных размеров с твердыми стенками, в котором частицы полностью и равномерно заполняют весь объем. Чисто гидродинамические силы в режиме стоксовского течения обладают таким свойством, что при интенсивном движении частицы могут сближаться друг с другом не соприкасаясь. Особенность стесненного режима движения состоит в том, что стенки сосуда могут воздействовать на частицы, далеко отстоящие от них (т.е. оказывать дальнее воздействие), меняя при этом тип реологического уравнения. В этом случае методы, развитые для суспензии, находящейся в нестесненном состоянии, оказываются неэффективными. Природа дальнего воздействия проявляется в том, что образуются кластеры частиц, которые передают импульс непосредственно друг другу во всем кластере одновременно. В результате оба режима (стесненный и нестесненный), возможно, описываются разными реологическим уравнениями или, по крайней мере, разными режимами, вытекающими из одного и того же реологического уравнения.

Если нестесненный режим допускает какой-то анализ математическими средствами, то о стесненном движении мы практически ничего не знаем, кроме некоторых чисто качественных рассуждений. В данном разделе мы приводим краткий обзор некоторых результатов исследований суспензии, связанных с задачей усреднения. Почти все они касаются относительно более простого режима нестесненного движения. Между тем с точки зрения процедуры усреднения наибольший интерес представляет именно режим стесненного движения. Изучение различных подходов позволяет понять характер возникающих при этом трудностей, в частности, проблему усреднения по времени.

Сформулируем краевую задачу для каждого режима. Пусть область представляет собой вязкую плоскость за вычетом включений. В этой области справедливы уравнения гидродинамики Стокса,

:,,,,. (5.9) Здесь,– тензоры полных и девиаторных напряжений,– давление,– тензор скорости деформаций,– скорость,– коэффициент вязкости.

Пусть сосуд в режиме обтекания имеет форму куба, каждая грань которого перпендикулярна соответственно оси . Длина ребра кубамного больше среднего расстояния между частицами. Частицы равномерно заполняют его. На-той грани куба задается вектор напряжений(). Девиатор напряжений удовлетворяет граничному условию

при. (5.10) Здесь знаки + и – соответствуют противоположным граням.

Для свободных включений выставляются кинематические условия на границах жестких кругов и условия отсутствия суммарных сил и моментов, действующих на них,

,a)

,b) (5.11)

. с) Здесь,– поступательная скорость центров дисков и скорость углового их вращения , которые являются неопределенными величинами,– радиусы-векторы их центров,,– главные векторы сил и момента, действующие на частицы.

Более удобным для исследования является режим нестесненного движения, для которого получены точные решения и разработано большое количество приближенных и достаточно обоснованных методов. Однако уже сама формулировка задачи усреднения для этого режима вызывает затруднение, поскольку состояние среды внутри облака частиц и на большом удалении от него – разное. Для нестесненного движения обычно задаются граничные условия на внутренних границах, т.е. на частицы действуют локальные силы и моменты

:,a)

,.b) (5.12) а на бесконечности задаются затухающие напряжения

при, где. (5.13) Здесь‑ второй инвариант девиатора напряжений.

При условии (5.13) не совсем понятно как можно определить средние напряжения, входящие в реологическое уравнение. Тем не менее, такой режим движения смесей существует, и требует своего корректного описания. Например взбаламученный морской или речной ил создает облако возмущенного движения, которое со временем оседает. Динамика его соответствует краевой задаче нестесненного движения смеси. В этой связи мы рассматриваем различные методы усреднения адаптированные к тому или иному режиму движения смесей.

Метод отражений.В нестесненном режиме были получены точные решения для двух частных случаев движения двух одинаковых сфер – вращение частиц вокруг их центра масс (Джеффри 1915г.), а также – для обтекания их вдоль линии их центров (Стимпсон и Джеффри, 1926г.). Через 40 лет было получено также общее решение в бигармонических рядах, вычисление которых уже требует численных расчетов. При сближении частиц в решениях возникают особенности, связанные с возникновением смазочного слоя между частицами.

Среди приближенных методов наибольшее распространение получил метод отражений. Суть его сводится к методу последовательных приближений. В силу линейности уравнений Стокса скорость и давление могут быть представлены в виде аддитивных разложений по малому параметру (где– средний радиус частиц)

,. (5.14)

В качестве первого члена разложения берется сумма гидродинамических полей в приближении малой концентрации. В следующем приближении берется аналогичная сумма полей, которая в граничных условиях компенсирует те невязки (т.е. возмущения), которые возникают в членах первого приближения и т.д. При построении очередного по порядку члена разложения каждый раз приходится решать аналогичную краевую задачу с соответствующими граничными условиями на границах частиц.

Таким методом, в принципе, можно решать задачи для любого числа частиц. Однако на практике он оказался удобным только лишь для двух частиц. Это связано с использованием специальной бифокальной системы координат. Было получено хорошее совпадение с точными аналитическими решениями вплоть до значений .

Метод коллокаций. Для систем, состоящих из многих частиц более успешным оказался метод усреднения, который представляет собой некоторую разновидность метода отражений. Суть его состоит в том, что требование выполнения граничных условий на всех внутренних границах заменяется более слабым требованием соблюдения их только в конечном числе точек этих границ. Этот метод оказался весьма успешным в тех случаях, когда система частиц обладает какой-то симметрией или симметрией какого-то другого рода. В этих случаях граничные условия в отдельных точках обобщаются на случай линий или поверхностей, что сразу повышает точность метода и снижает число итераций. Метод коллокаций чувствителен к выбору точек, что особенно неудобно для подвижных частиц и является очень громоздким. В этом отношении наиболее эффективным представляется предложенный Струминским метод сосредоточенных сил и моментов.

Метод точечных сил и моментов. Суть метода состоит в приближенном представлении возмущений, вносимых частицами, силовыми точечными источниками и моментами. Идея метода основана на простом факте. Поле скоростей и давлений, вызванное точечным источником силы, описывается уравнением

. (5.15) Здесь– дельта-функция.

Лэмб впервые показал, что на удалении от источника поле скоростей и давления, которое является решением этого уравнения, точно совпадает с полем, порождаемым движением одиночной сферы. Идея моделирования точечной силой оказалась очень плодотворной и неоднократно применялась в различных схемах коллективного движения частиц. Она долгое время оставалась невостребованной в связи с тем, что математическое обоснование ее и оценка невязки в отличие от методов отражения и коллокаций были недосягаемы, пока Струминский и его коллеги не нашли решение данной проблемы. Главное достоинства его метода состоит в том, что возмущения от каждой частицы являются аддитивными и потому допускают стандартные расчеты методом последовательных приближений. Решение ищется в виде разложения по малому параметру , гдерадиус частицы,– характерное расстояние между ними. Хотя сами расчеты и являются достаточно громоздкими и не совсем удобными при аналитических преобразованиях, этим методом в пределах его применимости можно получить сколь угодно точные выражения не только для скоростей частиц, но и для скоростей и давления в промежутке между частицами.

Метод Струминского перестает работать при . При достижении этого порога частицы либо соприкасаются, либо (если молекулярными силами можно пренебречь) между ними возникает тонкий гидродинамический слой, который препятствует их дальнейшему сближению. Это и есть стесненный режим движения. При наличии стенок и нетривиальных граничных условий на них стесненный характер движения проявляется в том, возникает дальнее взаимодействие между частицами, которое качественно меняет тип реологического уравнения.