2. Фильтрационная составляющая решения во внешней области

Задача о конечной трещине.Исследуем поведение решения уравнения (1.17) в окрестности трещины, считая, что давление жидкости в трещине зависит только от времени

:. (2.1)

Окрестность трещины включает сам разрези окружающую его малую область (:,), которая состоит из регулярной части (:,) и окрестности концевых точек. Рассмотрим поведение решения в. Примем следующие предположения. Будем считать, что в областирешение уравнения пьезопроводности (1.13) допускает разделение переменных

, (2.2) где– функция времени,– функция координат. Все остальные величины также допускают разделение переменных. Второе предположение утверждает, что, кроме того, справедливы неравенства

. (2.3)

Справедливость сделанных предположений будет подтверждена непротиворечивостью полученных результатов.

Подставляя выражение (2.2) в уравнение (1.13), приходим к форме уравнения Гельмгольца

, где,. (2.4) Здесь точка сверху означает производную по своему аргументу. Аналогичным образом преобразуются граничные условия (1.4), (1.5)

:. (2.5)

при. (2.6)

В явном виде данное уравнение не зависит от времени. Время входит в него как параметр через граничные условия, поскольку оба размера трещины зависят от времени. Точнее говоря, размеры трещины зависят от приложенного давления в скважине и скорости его возрастания.

Произведя упрощение в (2.4) с помощью условия (2.3), приходим к обыкновенному дифференциальному уравнению

. (2.7)

В регулярной области уравнение (2.7) с граничным условием (2.5) допускает решение, обладающее свойствами симметрии,

. (2.8)

Можно исследовать также асимптотику на бесконечности. В этом случае удобно перейти к полярным координатам. Поскольку на бесконечности возмущение обладает цилиндрической симметрией, то уравнение (2.2) упрощается

. Затухающее на бесконечности решение этого уравнения дается цилиндрической функцией мнимого аргумента

, где– неопределенная константа.

Подставляя (2.6) в (1.17), в регулярной области получаем приближенное равенство

. (2.9)

В силу неравенства (2.3) уравнение (2.9) упрощается

и с учетом (1.10b) легко интегрируется

.

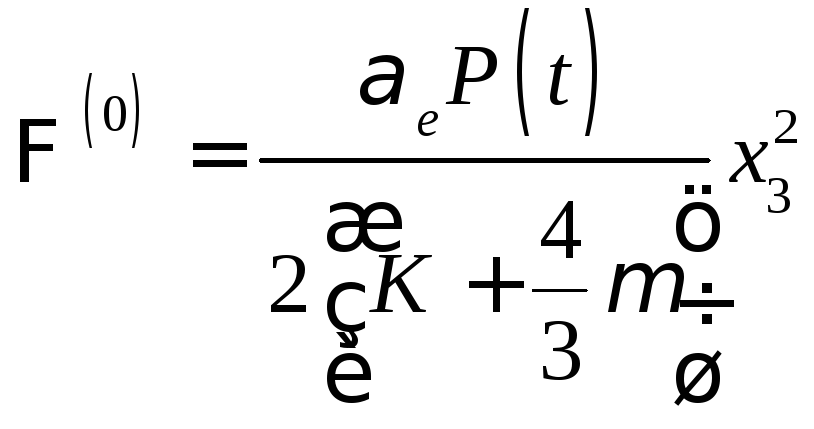Это решение удовлетворяет граничному условию на трещине

:,. (2.10)

Как и следовало ожидать, выбор граничного условия в (1.10) для потенциала типа Дирихле или Неймана не имеет значения.

В силу (2.10) граничные условия для напряжений (1.15), (1.16) упрощаются и сводятся к простой форме

:,. (2.11)

В силу неравенства (2.3) скорость фильтрации направлена перпендикулярно границе, и на границе выполняются следующие условия

:, .(2.12)

Граничные условия (2.11), (2.12) позволяют решать задачу для упругой составляющей, уже независимо от фильтрационной составляющей.

3. Упругая составляющая решения во внешней области

Рассмотрим вспомогательную плоскую задачу классической теории упругости для упругой составляющей с граничными условиями на разрезе (1.15). Полагая , с помощью комплексных потенциаловиперейдем в комплексное представление:

, ,

, ,

, .Здесь– комплексный главный вектор усилий первой составляющей, приложенных к контуру, соединяющему точкии. При движении откположительная нормаль находится справа от контура. Черта сверху обозначает комплексное сопряжение, а штрих означает производную по своему аргументу.

Производные комплексных потенциалов ограничены на бесконечности, а сами потенциалы обладают свойствами симметрии

,,,.

В граничные условия для упругой составляющей в силу (2.11) не входят касательные напряжения. В этом случае в силу свойств симметрии имеем соотношение, справедливое на всей оси

при.

Из этого соотношения и условия затухания на бесконечности (1.5) следует равенство на всей плоскости (как следствие решения задачи Дирихле)

. (3.1)

Из (3.1) следует, что на трещине выполняется условие

:. (3.2)

Рассмотрим частный случай, когда давление в трещине зависит только от времени

:. (3.3)

В силу (2.12) обе составляющие порового давления также являются функциями только времени

:,,.

Комбинируя (1.12b) и (3.3) (и учитывая (2.11) и (3.2)), приходим к граничному условию для нормальных напряжений упругой составляющей

:, .(3.4)

С другой стороны граничное условие (2.11) при тех же условиях имеет вид

:. (3.5)

или в комплексной форме

:. (3.6)

Сравнивая соотношения (3.4) и (3.5), получаем

, .

Краевая задача (3.6) имеет известное решение

,,a)

,.b) (3.7)

С учетом (3.7) получаем выражение для смещения упругой составляющей на границе

:. (3.8)

Вертикальная составляющая на границе терпит разрыв, который дается выражением

:. (3.9)

В силу (1.10b,c) фильтрационная составляющая смещения на границе непрерывна. Поэтому скачок упругой составляющей смещения дает полное раскрытие трещины

:. (3.10)

Граничное условие (1.14) также упрощается

:. (3.11)

Таким образом, с чисто формальной точки зрения задача по-прежнему остается связанной. Однако связанность проявляется тривиальным образом – с помощью поправочного коэффициента в граничных условиях (3.5), (3.11). Эта поправка не мешает решать несвязанные задачи для обеих составляющих порознь, независимо друг от друга.

В стационарном режиме фильтрационное уравнение (1.13) упрощается

.

В этом случае можно также представить в комплексной форме фильтрационную составляющую. В силу (1.10а), (1.17) и последнего уравнения гидродинамический потенциал является бигармонической функцией везде за исключением особых точек. Согласно [Мусхелишвили, 1966] сам потенциал и его градиент могут быть представлены через комплексные потенциалы

,a)

,,b) (3.12)

Выразим также фильтрационную составляющую комплексных напряжений через потенциалы

. (3.13)

Заметим, что комплексное представление напряжений (3.12b), (3.13) напоминают аналогичные соотношения для упругой составляющей, за исключением первого члена в выражении для смещения. Для того, чтобы удовлетворить граничному условию (1.16b), положим

или. (3.14)

Выпишем полные смещения и напряжения с учетом (3.1) и (3.14)

a)

b) (3.15)

Граничное условие (1.19) в комплексных потенциалах принимает вид

:. (3.16)