
26 Курс механики пороупругих сред Лекция № 12. Основные уравнения механики пороупругих сред
Различные формы представления уравнений движения пороупругих сред. Вывод уравнения пьезопроводности. Исследование усложненных моделей с многофазным флюидом и с перекрестными членами в уравнениях фильтрации.
1. Общие уравнения движения
Упругие деформации всех известных
горных пород не могут превысить величину
![]() .
При превышении этого значения породы
подвергаются разрушению. Малое значение
упругих деформаций приводит к существенному
упрощению теории пороупругости. В
предыдущей лекции уравнения механики
пороупругости выведены исходя из
термодинамических принципов. В
классической механике пороупругости
горных пород предполагается, что упругие
деформации скелета и объемные упругие
деформации флюидов малы, а средние
смещения скелета и флюидов по элементарному
объему одного порядка
.
При превышении этого значения породы
подвергаются разрушению. Малое значение
упругих деформаций приводит к существенному
упрощению теории пороупругости. В
предыдущей лекции уравнения механики
пороупругости выведены исходя из
термодинамических принципов. В
классической механике пороупругости
горных пород предполагается, что упругие
деформации скелета и объемные упругие
деформации флюидов малы, а средние
смещения скелета и флюидов по элементарному
объему одного порядка
![]() ,
,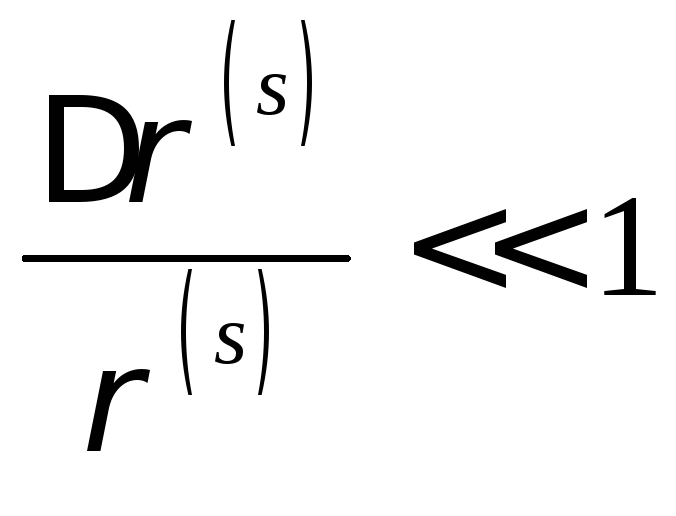 , a)
, a)
 ,
,![]() .b) (1.1)
.b) (1.1)
Соотношения (1.1b) могут быть нарушены по двум причинам. Одна из них вызвана конечными упругими деформациями объема флюида, характерными для газовой фазы. В этом случае
 . (1.1с)
. (1.1с)
Вторая причина может быть связана с процессами течения и вытеснения одной флюидной фазой другую
![]() . (1.2)
. (1.2)
Процессы вытеснения в теории пороупругости
с многофазным флюидом предполагают
существование двух временных масштабов
– быстрого и медленного времени
![]() и
и![]() .
В течение быстрого времени имеют место
собственно пороупругие процессы, т.е.
выполняются соотношения (1.1b).
В течение медленного времени происходят
процессы замещения и вытеснения флюидных
фаз. В этом случае мы имеем вырождение
уравнений пороупругости и переход к
теории фильтрации в пористой среде с
жестким скелетом. В данном разделе мы
ограничимся анализом пороупругих
процессов в быстром режиме.
.
В течение быстрого времени имеют место
собственно пороупругие процессы, т.е.
выполняются соотношения (1.1b).
В течение медленного времени происходят
процессы замещения и вытеснения флюидных
фаз. В этом случае мы имеем вырождение
уравнений пороупругости и переход к
теории фильтрации в пористой среде с
жестким скелетом. В данном разделе мы
ограничимся анализом пороупругих
процессов в быстром режиме.
Уравнения пороупругости можно разделить на две группы. К первой группе относятся соотношения для напряжений. Обобщенное выражение для тензора полных напряжений и понятие тензора эффективных напряжения для таких сред впервые были предложены Айфантисом [Wilson,Aifantis, 1982]. Флюидные процессы описывают законы фильтрации. Наиболее известным и широко распространенным является закон Маскета-Леверетта для каждой фазы
![]() ,
,![]() a)
a)
![]() ,
,![]() ,b)
,b)
![]() ,
,![]() ,
,![]() , с) (1.3)
, с) (1.3)
 ,
,
![]() ,
,![]() .d)
Здесь
.d)
Здесь![]() – поровые давления флюидных фаз,
– поровые давления флюидных фаз,![]() – пористость,
– пористость,![]() – коэффициенты при фазовых поровых
давлениях, которые определяются
спецификой конкретных моделей,
– коэффициенты при фазовых поровых
давлениях, которые определяются
спецификой конкретных моделей,![]() ,
,![]() – скорость флюидных фаз и фазовая
скорость фильтрации,
– скорость флюидных фаз и фазовая
скорость фильтрации,![]() – коэффициент вязкости флюидной фазы,
– коэффициент вязкости флюидной фазы,![]() – абсолютная фазовая проницаемость
соответствующей фазы флюида,
– абсолютная фазовая проницаемость
соответствующей фазы флюида,
![]() – относительные фазовые проницаемости,
которые нормируются таким образом, что
– относительные фазовые проницаемости,
которые нормируются таким образом, что![]() ;
;![]() – абсолютная проницаемость пористой
среды.
– абсолютная проницаемость пористой
среды.
Вывод определяющих соотношений из термодинамики необратимых процессов допускает более общую форму закона фильтрации, включающую в себя перекрестные члены,
 ,
,![]() ,
,![]() . (1.4)
. (1.4)
Принятый нами подход гарантирует нам, что эти определяющие соотношения не противоречат общим физическим принципам даже в более общем случае, когда скелет подвергается конечным деформациям. Проблема заключается лишь в том, чтобы отождествить и сам закон многофазной фильтрацией и перекрестные члены в нем с конкретными физическими процессами в пороупругой среде, моделирующей реальные углеводородные месторождения. Более того, определяющие соотношения не исчерпываются гидродинамическими уравнениями. Кроме них есть еще уравнения состояния для твердой фазы и уравнения связи. Мы должны быть уверены в том, что наши уравнения движения адекватно описывают именно ту среду, которую мы хотим изучить. Смысл дальнейших рассуждений как раз и состоит в том, чтобы прояснить эти вопросы.
Определяющие уравнения должны быть дополнены уравнениями состояния скелетной и флюидной фаз и условием фазового равновесия. Для простоты ограничимся лишь однофазным скелетом
 ,
, ,
,
![]() ,
,![]() , (1.5)
где
, (1.5)
где![]() и
и![]() – истинные объемные модули скелетной
и флюидной фаз, символ
– истинные объемные модули скелетной
и флюидной фаз, символ![]() означает отклонение данной величины
от равновесного (ненапряженного)
состояния, которое отмечается нижним
нулевым индексом. В силу линейности
уравнений состояния фаз истинные и
осредненные уравнения – идентичны.
означает отклонение данной величины
от равновесного (ненапряженного)
состояния, которое отмечается нижним
нулевым индексом. В силу линейности
уравнений состояния фаз истинные и
осредненные уравнения – идентичны.
Вторую группу уравнений составляют
соотношения баланса массы фаз. Каждая
фаза может состоять из компонент.
Компоненты характеризуется приведенной
плотностью
![]() и массовой концентрацией
и массовой концентрацией![]() .
Для них имеем уравнения
.
Для них имеем уравнения
![]() ,
,![]() , а)
, а)
![]() . b) (1.6)
Здесь
. b) (1.6)
Здесь![]() – скорость фазовых превращений компонента
– скорость фазовых превращений компонента![]() от фазы
от фазы![]() к фазе
к фазе![]() .
.
Уравнения движения пороупругой среды (1.3) выражается в смещениях уравнением, аналогичным уравнению для однофазного флюида,
![]() . (1.7)
. (1.7)
Поскольку уравнения непрерывности содержат производную по времени, то краевые условия должны включать в себя начальное условие. Мы игнорируем начальное напряженное состояние. Поэтому начальные значения смещений, деформаций и напряжений равны нулю. Ненулевое начальное условие формулируется для фазовых поровых давлений
![]() ,
,![]() при
при![]() . (1.8)
. (1.8)
Граничные условия пороупругой задачи (так же, как и уравнения движения) могут быть в напряжениях или в смещениях (или быть смешанного типа)
![]() :
:![]() ,
,![]() илиa)
илиa)
![]() ,b) (1.9)
где
,b) (1.9)
где![]() – вектор единичной нормали.
– вектор единичной нормали.
В граничных условиях для флюидных фаз могут фигурировать фазовые поровые давление или скорости фильтрации. Тип этих условий может быть самым разнообразным в зависимости от физической постановки задачи. Ниже в иллюстративных целях приведен один из возможных вариантов этих условий. В частности, на границе могут задаваться условия отдельно для каждой фазы
![]() :
:![]() илиa)
илиa)
![]() .b) (1.10)
Здесь
.b) (1.10)
Здесь![]() ,
,![]() ,
,![]() и
и![]() – граничные значения соответствующих
величин.
– граничные значения соответствующих
величин.
Краевые условия (1.9) – (1.10) носят общий характер. Особенность задач с двухфазным флюидом состоит в том, что могут появиться внутренние границы, на которых терпят разрыв проницаемость и насыщенности фаз. На этих граница непрерывны поровое давление и масса каждой фазы [Нигматулин, 1987; Николаевский, 1996], кроме того, непрерывны тангенциальные компоненты скорости скелета,
![]()
![]() ,a)
,a)
![]() ,b) (1.11)
,b) (1.11)
![]() ,
,![]() . с)
Здесь
. с)
Здесь![]() – скачок величины
– скачок величины![]() на граничной поверхности,
на граничной поверхности,![]() – скорость внутренней границы,
направленная по нормали,
– скорость внутренней границы,
направленная по нормали,![]() – касательные к границе единичные
векторы.
– касательные к границе единичные
векторы.
В большинстве прикладных задач подземной гидродинамики (как раздела нефтяной геофизики) отсутствуют фазовые переходы между скелетом и флюидом, т.е. не рассматриваются модели частичного плавления среды. Полная пористость на границе непрерывна, а условие (1.11с) упрощается
![]() :
:![]() , а)
, а)
![]() .b) (1.12)
.b) (1.12)
Формально система уравнений пороупругости замкнута и может быть решена, по крайней мере, численно. Однако решение, как правило, имеет практическую ценность только тогда, когда оно может быть подвергнуто качественному анализу. В этой связи уравнения движения должны быть преобразованы к наиболее удобной для исследования форме. В частности, эволюционные процессы можно исследовать с помощью уравнения пьезопроводности. Как правило, вывод уравнения пьезопроводности связан с некоторыми специфическими величинами и системой малых параметров. Выявит эту специфику, опираясь только на термодинамические подходы и чисто математические методы осреднения весьма затруднительно. Наиболее конструктивным и часто используемым методом построения различных вариантов модели пороупругих сред является мысленный эксперимент и эвристические рассуждения. В этой связи представляет интерес поиск некоторых общих подходов и методов в данном направлении. С методической точки зрения разумно при этом опираться на простейший вариант теории пороупругости Био.
Вырожденные ситуации. В частном случае, когда одна из фазовых проницаемостей значительно превышает проницаемость всех остальных фаз
![]() ,
,![]() , (1.13)
малопроницаемые
флюидные фазы в режиме пороупругих
движений практически остаются неподвижными
и составляют часть скелетной фазы. Все
движение определяется наиболее подвижной
флюидной фазой и сводится к классической
схеме движения пороупругой среды с
однофазным флюидом и многофазным
скелетом. При вычислении его упругих
модулей следует применять механику
композитов.
, (1.13)
малопроницаемые
флюидные фазы в режиме пороупругих
движений практически остаются неподвижными
и составляют часть скелетной фазы. Все
движение определяется наиболее подвижной
флюидной фазой и сводится к классической
схеме движения пороупругой среды с
однофазным флюидом и многофазным
скелетом. При вычислении его упругих
модулей следует применять механику
композитов.
Пусть, например, в качестве флюида выступает газожидкостная смесь. Здесь возможны различные ситуации. Пузырьки газа могут оказаться защемленными в узких порах, и тогда они составляют часть скелета. В этом случае фильтруется только флюид, а сжимаемость многофазного скелета определяется газовыми пузырьками и может оказаться очень большой. Если же газ свободно фильтруется, то возможны два варианта. Если движение газа происходит в пороупругом режиме, то жидкость не успевает вытекать из элементарного объема, и она входит в состав скелета. В этом случае применимы уравнения Лейбензона. В другом варианте имеют место медленные движения газовой фазы в квазистатическом режиме, а пороупругие процессы возможны только в жидких фазах. Во всех перечисленных случаях вырождение проявляется в том, что фактически уменьшается число флюидных фаз, участвующих в пороупругих процессах в силу особых свойств этих фаз. При этом реально эти фазы сами по себе никуда не исчезают, а только меняется их статус в пороупругой среде.
Наконец, к вырождению уравнений движения пороупругости приводит медленное вытеснение друг друга флюидными фазами. Пусть фазовые проницаемости и вязкости флюидов хотя и различаются, но, тем не менее, остаются в пределах одного порядка (т.е. нет других видов вырождения)
![]() ,
.
,
.![]() (1.15)
(1.15)
Как уже было показано, в приведенных
выше выражениях величины зависят от
двух времен – быстрого и медленного.
Быстрое время будем обозначать как
![]() ,
а медленное время – как
,
а медленное время – как![]() .
Характерные величины времен
.
Характерные величины времен![]() и размер
и размер![]() быстрых процессов связаны соотношением
быстрых процессов связаны соотношением
![]() ,
откуда
следует выражение для масштаба быстрого
времени
,
откуда
следует выражение для масштаба быстрого
времени
 ,
где
,
где![]() – масштаб порового давления,
– масштаб порового давления,![]() – масштаб пороупругой области. Масштаб
медленного времени задается априори,
исходя из особенностей технологического
процесса вытеснения. Естественно, что
полные уравнения пороупругости содержат
малый параметр
– масштаб пороупругой области. Масштаб
медленного времени задается априори,
исходя из особенностей технологического
процесса вытеснения. Естественно, что
полные уравнения пороупругости содержат
малый параметр![]() ,
равный отношению этих времен
,
равный отношению этих времен
![]() .
.
Произведем оценку малого параметра. Из уравнений непрерывности фаз вытекает соотношение для масштаба медленного времени
 ,
где
звездочкой отмечены масштабы
соответствующих величин.
,
где
звездочкой отмечены масштабы
соответствующих величин.
В течение быстрого времени (оно находится в интервале от минут до суток) происходят пороупругие процессы, сопровождающиеся малыми упругими деформациями скелета. При этом в невырожденном состоянии (когда производной по времени можно пренебречь) смещение флюидов того же порядка, что и смещение скелета, т.е. является малым. В течение медленного времени происходит вытеснение одной фазы другой (например, вода вытесняет нефть). Масштаб медленного порядка многих месяцев. В этом режиме упругие деформации скелета малы, а смещения флюидных фаз достаточно большие.
При наличии многих масштабов пространства или времени актуальнымбудем называть тот масштаб, в котором разворачиваются интересующие нас события. В мономасштабной среде понятия актуальный и характерный масштабы совпадают. Одни величины (например, пористость) зависят только от быстрого времени, другие (например, насыщенность и поровое давление) зависят как от быстрого, так и от медленного времени. Существует стандартная процедура многомасштабного временного разложения, которая сводится к некоторому формальному приему. Он состоит в том, что быстрое и медленное времена рассматриваются как независимые аргументы. Поэтому, считая, что актуальным масштабом является медленное время, производную по времени можно представить следующим образом
![]() (1.16)
(1.16)
Заметим, что производная по времени входит только в уравнения непрерывности (1.6). Поэтому процедура временного разложения применима только к ним. Подставляя (1.16) в эти уравнения получаем
 ,
,![]() , а)
, а)
 .b) (1.17)
.b) (1.17)
Функции источников теоретически могут
зависеть как от быстрого, так и от
медленного времени. Произведем в (1.17)
разложение по малому параметру
![]() .
Выделим главные члены и отбросим малые
величины. Тогда приходим к уравнениям,
аналогичным (1.6) с той лишь разницей, что
теперь величины в нем зависят только
от быстрого времени
.
Выделим главные члены и отбросим малые
величины. Тогда приходим к уравнениям,
аналогичным (1.6) с той лишь разницей, что
теперь величины в нем зависят только
от быстрого времени
![]() ,
,![]() , а)
, а)
![]() .b) (1.18)
.b) (1.18)
Быстрые процессы характеризуются соотношениями (5.1.21). В следующем порядке теории возмущений получаем те же самые уравнения, только в режиме медленного времени.
![]() ,
,![]() , а)
, а)
![]() .b) (1.19)
.b) (1.19)
На первый взгляд уравнения (1.19) совпадают
с уравнениями (1.18). Однако есть существенные
отличия. Пористость и упругие характеристики
(например, объемное сжатие) не зависят
от медленного времени. Однако в медленном
режиме при многофазном флюиде возможно
вытеснение одной фазой другую. При этом
изменение фаз
![]() уже не является малым, и выполняются
соотношения (5.1.21). Кроме того, от медленного
времени зависят те величины, которые
выражаются через насыщенности. Поэтому
тип уравнений (1.18) и (1.19) разный. В
технологических процессах вытеснения
распределение давления обычно является
постоянной величиной и не зависит от
медленного времени, хотя и меняется в
пространстве. Пористость же определяется
геофизическими методами и тоже считается
известной. Неизвестными искомыми
величинами являются насыщенности,
фазовые поровые объемы и скорости.
уже не является малым, и выполняются
соотношения (5.1.21). Кроме того, от медленного
времени зависят те величины, которые
выражаются через насыщенности. Поэтому
тип уравнений (1.18) и (1.19) разный. В
технологических процессах вытеснения
распределение давления обычно является
постоянной величиной и не зависит от
медленного времени, хотя и меняется в
пространстве. Пористость же определяется
геофизическими методами и тоже считается
известной. Неизвестными искомыми
величинами являются насыщенности,
фазовые поровые объемы и скорости.
Аналогичные разложения производятся также в уравнениях фильтрации и других уравнениях механики пороупругих сред. Поскольку эти уравнения не содержат производные по времени, то, как правило, главные члены разложения дают те ж самые уравнения, т.е. оставляют их без изменения.
