9. Метод интегрирования условия Гюгонио

В данном разделе мы сформулируем необходимые и одно достаточные условия существования решения задачи Коши для фильтрационной составляющей. Идея доказательства по существу аналогична доказательству, приведенному в [1], откуда и заимствовано название этого метода. Однако ход рассуждений основывается на методе, предложенном в работе [2], который нам представляется более простым и прозрачным.

Рассмотрим области влияния иположительной и отрицательной полуосей начальной линии. Пересечение этих областей (как обозначим как область) является областью влияния начальной точки. Пусть,и– характеристики областей,и, и пустьисоответственно являются крайними характеристиками областейи, т.е. крайней левой для областикрайней правой для области. Тогда в областикрайней левой характеристикой будет, а крайней правой – характеристика. Согласно сказанному выше обе задачи будут эквивалентными, если характеристикане будет заходить в область, т.е.

. (9.1)

Согласно [2] в задаче 2 следует найти все решения характеристических уравнений и с помощью необходимых критериев отобрать только те из них, которые соответствуют решению с устойчивым разрывом. Если оно окажется единственным, то оно и будет искомым решением характеристических уравнений, на основе которого и строится решение задачи Коши. Построение областей ,ипроводится, следуя работе [1].

Вывод необходимых условий допустимости сильного разрыва, приведенный в работах [2 – 5], сводится к тому, что разрывы "размазываются", и затем предельным переходом доказывается устойчивость или неустойчивость данного разрыва. В частности, выводятся критерии устойчивости. Результат, вообще говоря, не должен зависеть от способа размазывания, однако, обычно процедура размазывания основана на замене гиперболических уравнений типа (2.2) параболическими уравнениями вида

. (9.2) с последующим предельным переходом.

Вводится понятие эволюционности системы уравнений. Суть его сводится к требованию корректной постановки задачи об устойчивости. При линеаризации уравнения (2.10), а также характеристических уравнений, возникает система линейных уравнений. Важно, чтобы число этих уравнений было бы не меньше, чем число неизвестных. Для этого необходимо, чтобы характеристики, заканчивающиеся на траектории разрыва, начинались на граничной линии, а не на самой траектории разрыва.

На основе этих соображений выводятся два конкретных необходимых условия допустимостисильного разрыва [2]. При их нарушении устойчивый разрыв невозможен. Определим функциюсоотношением

, (9.3) где– неопределенная константа.

Первое условие допустимости предполагает, что граничные значения насыщенности на разрыве идолжны быть соседними нулями функции. Другими словами, между этими нулями не должно быть ни одного другого нуля этой функции.

Второе условие сводится к соотношению

при,. (9.4) Подчеркнем, что знаки минус и плюс связаны с предельными значениями начальных функций при приближении к разрыву соответственно до разрыва и после него. Поскольку в области физического решения происходит пересечение областей влиянияи, то эти знаки меняются местами по сравнению с их положением на начальной линии. Если, то величиныиодновременно должны быть или не больше или не меньше, чем.

Использование обоих условий приводит к следующему результату. Разрыв соответствуют хорде на рис. 1, которая пересекает кривую в двух точках –и. Хорда, которая пересекает кривуюв точке, нарушает первое условие. Нули функциине являются соседними нулями: между ними есть еще один нуль, а именно точка. Следовательно, положение изображающей точки выше точкине является устойчивым. Другими словами, в начальный момент изображающая точка на рис. 1 мгновенно перескакивает с положениядо положения. Точкана рис. 1 соответствует касанию хорды кривой

. (9.5) Эта точка соответствует решению классической задачи Баклея-Леверетта, в которой траектория разрыва совпадает с характеристикой, сам разрыв является постоянным и равным.

В нашем случае все точки на кривойна диаграмме рис. 1, находящиеся ниже точки, удовлетворяют обоим необходимым условиям. В силу этих условий движение точкипо кривой) начинается с точки, причем она может двигаться только вниз от нее или стоять на месте. В силу (2.7с) точкана этой диаграмме обязательно движется вниз при движении вдоль характеристики и при удалении от начала координат, независимо от характеристик.

Решение характеристических уравнений (2.7) с условием (2.8) в каждой из областей ,иимеет вид

,,, а)

,,,b) (9.6)

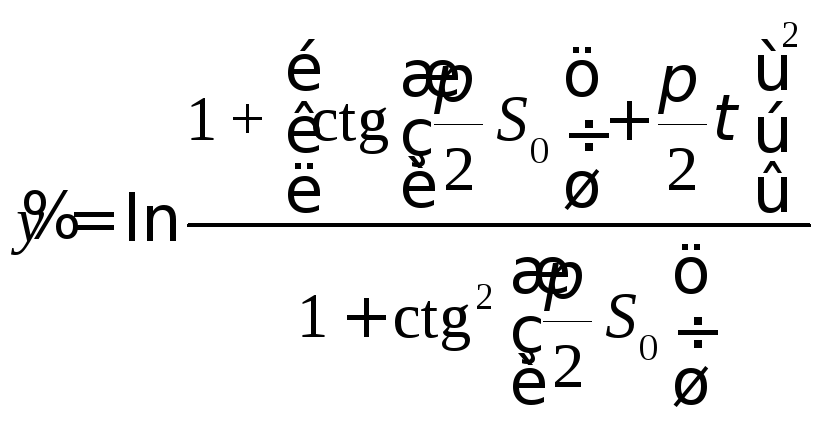,. с)

.

Фазовый портрет семейства характеристик всех трех областей представлен на рис. 2. Решение в областиполучаем, сдвигая характеристику (9.6а) влево от своего крайнего правого значения. Насыщенность зависит от времени, но не зависит от координаты. В областивеличиныитождественно равны нулю. С помощью (9.6) найдем характеристики, ограничивающие область. Характеристикииможно получить, полагая в (9.6с),

,, а)

,.b) (9.7)

В области характеристиками являются вертикальные линии, которые обязательно упираются в траекторию разрыва. Характеристика, которая совпадает с осью, удовлетворяет условию (9.1). Следовательно, эквивалентность решений задач 1 и 2 доказана. В силу второго соотношения (9.6b) на разрыве насыщенность падает до нуля, и выражение (8.5а) упрощается

. (9.8)

Область соответствует тривиальному физическому решению с равной нулю насыщенностью. Нетривиальное физическое решение содержится в области, которая расположена между характеристикойи траекторией разрыва. В силу (9.8), (9.5) и (2.7b) в окрестности начальной точки имеем соотношения

. (9.9)

Это означает, что траектория разрыва начинается в области. Затем она обязательно пересекает характеристикуи входит в область. В самом деле, если она не пересечет кривую, то начальное условие никогда не сможет повлиять на решение, что противоречит принципу эволюционности. Принцип эволюционности требует также, чтобы характеристики исходили из точки разрыва начальной линии, на которой насыщенность должна меняться в пределах. Это означает, что областьпредставляет центрированное решение, в котором все характеристики исходят из начальной точки. Остальные точки этой области описываютволну разрежения, т.е. представляют собой гладкое решение. В точке, в которой траекториявходит в область, выполняются одновременно равенства (9.8), (9.9). Этой точкой может быть только точка, в которой характеристика областикасается траектории разрыва.

Все проведенные рассуждения имеют простую геометрическую интерпретацию. Можно утверждать, что в первый момент времени изображающая точка на диаграмме рис. 1 мгновенно меняет значение насыщенности с 1 до . В окрестности начального момента времени решение совпадает с классическим решением Баклея-Леверетта. Эта ситуация отражена на рис. 3, на котором представлен фазовый портрет семейства характеристик. Далее движение начинается с точки, (которая соответствует устойчивому разрыву) вниз по указанной диаграмме в сторону уменьшения.

Фазовый портрет характеристик, показанный на рис. 2, отличается от аналогичного фазового портрета в случае , исследованном в [1]. В последнем случае траектория разрывавсегда находится в областии не выходит за ее пределы. Как видно из этого рисунка, все характеристики, упирающиеся в траекторию разрыва, начинаются на начальной линии в физической области или на начальной линии области. Ни одна из указанных характеристик не начинается на начальной линии в области(если исключить из нее начальную точку). Этот факт также соответствует принципу эволюционности. Он означает, что мы выбрали правильное решение характеристических уравнений.

Главное отличие данной задачи от задачи в работе [1], связано с особыми свойствами функции , которое приводит к различию решений. Оно заключается в том, что в нашем случае траектория разрыва не расположена целиком внутри области, а входит в нее лишь на некотором удалении от граничной точки. Из этого факта также следует, что при стремлении к начальной точке для насыщенности на разрыве должно выполняться условие (2.15b), которое нами было уже ранее выведено

при,(при,). (9.10)

Для нахождения решения задачи Коши в области исключим величинув выражениях (9.6с)

или а)

.b) (9.11)

Разрешая (9.11), получаем решение в одной из эквивалентных форм

, а)

,b) (9.12)

. с)

Эти формулы включают в себя также и нефизические решения, связанные с неоднозначностью решений характеристических уравнений. В частности, выражения для являются двузначным. При выводе (9.12b) мы ввели лишнее решение, которое исключили, взяв знак минус перед корнем в этом выражении. Поэтому выражение (9.12b) однозначно. В то же самое время выражения (9.12а) и (9.12c) являются двузначными, поскольку обратная функция кв физической области имеет два значения. Двузначность выражения (9.12а) соответствует двузначности обратной функции. Асимптотическое условие (9.10) позволяет нам выбрать знак + в выражении (9.12а) и соответствующее значение в (9.12с).

Таким образом, мы выбрали единственное решение задачи Коши в некотором классе решений и показали, что разрыв удовлетворяет необходимым условиям устойчивости. В силу теоремы единственности это и есть единственное решение. Траекторию разрыва получаем, интегрируя уравнение (9.8) с учетом (9.12). Выберем участки неоднозначности, прилегающие к этой траектории таким образом, чтобы они удовлетворяли условию эволюционности.

Уравнения теплопереноса. Уравнение теплопереноса является линейным, что упрощает рассуждения. Для них семейство характеристик и решение задачи Коши строятся стандартным способом. В начальной точке насыщенность и температура терпят разрыв, что приводит к неопределенности начальных значений температуры и всего решения уравнения теплопереноса. Эта проблема и ее решение были обсуждены выше.