8. Анализ постановки задачи

Преобразование исходной задачи. С помощью замены

,,,

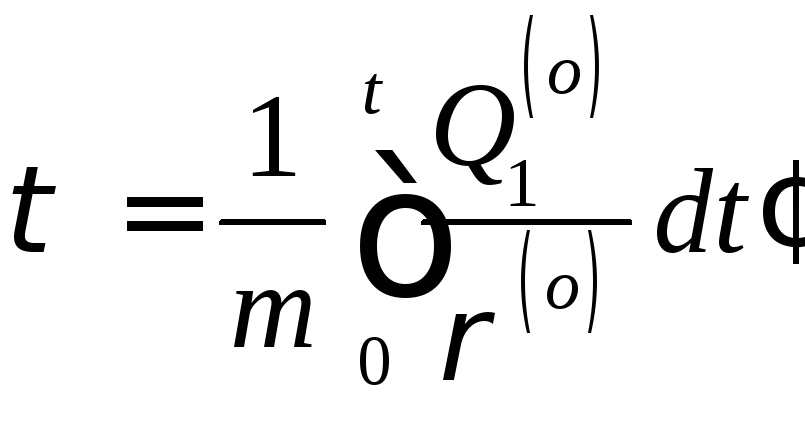,(8.1) перейдем к безразмерным переменным и преобразуем уравнения (7.8b), (7.9) и краевые условия (7.4) к более простой форме

,,. (8.2)

,,. (8.3)

,при,, а)

,при,,.b) (8.4)

Точно также преобразуются и условия Гюгонио (8.10) и (8.11)

, а)

,.b) (8.5) В новых переменных коэффициенты уравнения (8.2) и его правая часть зависят только от насыщенности и не зависят от координаты и времени. Задачу (8.2) – (8.5) будем называть задачей 1.

Преобразуем задачу 1 к стандартной форме задачи с одним начальным условием. С этой целью продолжим решение в нефизическую область и определим в этой области начальные условия, которые совместно с уравнениями (8.2), (8.3) представляют собой задачу Коши, которую назовем задачей 2,

,при,,, а)

,при,.b) (8.6) Значение насыщенности в начальной точке при,заранее не задается. Оно будет определено в процессе исследования задачи.

Заметим, что фильтрационное уравнение можно решать независимо от теплового уравнения, что упрощает рассуждения. Выпишем систему характеристических соотношений для уравнений (8.2) и (8.3)

,. Из них вытекают характеристические уравнения

, а)

,b) (8.7)

или. с)

, а)

.b) (8.8) с начальными условиями

при, где,– кусочно-непрерывные начальные функции с выколотой начальной точкой:

,при,, а)

,при,.b) (8.9)

Области влияния определяются для каждого участка гладкости разрывного начального условия (8.8), т.е. полуоси иимеют свои области влияния. Если принять значение функции Баклея-Леверетта согласно (8.14а), то уравнения (8.7) принимают вид

, а)

,b) (8.10)

. с)

Точно также конкретизируются материальные функции ив уравнении (8.38)

,.

Обе задачи в физической области, т.е. при эквивалентны, если выполнено условие. Область определимости задачи 1 должна включать в себя область влияния в задаче 2 положительной полуоси, и область влияния выколотой концевой точки. В самом деле, как следует из определения этих областей влияния и по их построению характеристики в них совпадают, если только из точки,на плоскостине выходит хотя бы одна характеристика, лежащая в нефизической области задачи 2. Поскольку во всех случаях решение строится из характеристик по одному и тому же рецепту, то отсюда и следует упомянутая выше эквивалентность. Следовательно, нам достаточно доказать существование единственного решения в задаче 2 и убедиться, что характеристики в пространствеудовлетворяют указанному условию.

Решение уравнения (8.2) содержит один сильный разрыв насыщенности, а решение уравнения (8.3) содержит два сильных разрыва температуры, которые движутся с разными скоростями. Физическая причина разрывов заключается в том, что начальные условия не согласованы с граничными условиями. Поэтому решение описывается аппаратом обобщенных функций. В начальный момент разрывы температуры накладываются друг на друга. Это создает особенность, характерную для произведения обобщенных функций. Математическая природа этой особенности такова, что решение теряет единственность. Для получения единственного решения необходимо использовать некоторые дополнительные физические соображения относительно процессов происходящих в начальной пространственно-временной точке. Они заключаются в том, что тепловой режим в этой точке соответствует установившимся фильтрационным процессам. Другими словами, пока на данном участке закончатся неравновесные тепловые процессы, сильный разрыв насыщенности (берущий начало в начальной точке) успеет уйти далеко от границы. Поэтому второй разрыв температуры отстает от разрыва насыщенности, которая остается на нем непрерывной. В этом случае уравнение (8.5b) упрощается

, скачок температуры равен скачку начальной функции температуры, а один из факторов неопределенности снимается.

Далее температурная составляющая решения будет формироваться в условиях непрерывного решения для фильтрационной составляющей. Дискретизация дифференциальных уравнений при численных расчетах эквивалентна некоторой процедуре регуляризации. Ее следует провести таким образом, чтобы учесть указанное условие. Следовательно, указанные дополнительные физические соображения должны быть заложены в самом алгоритме.

Асимптотика в окрестности начальной точки.В этой связи исследуем окрестность начальной точки на плоскости, которая является особой точкой задачи Коши для обоих уравнений (8.2) и (8.3). Рассмотрим предельный случай малого источника

,.

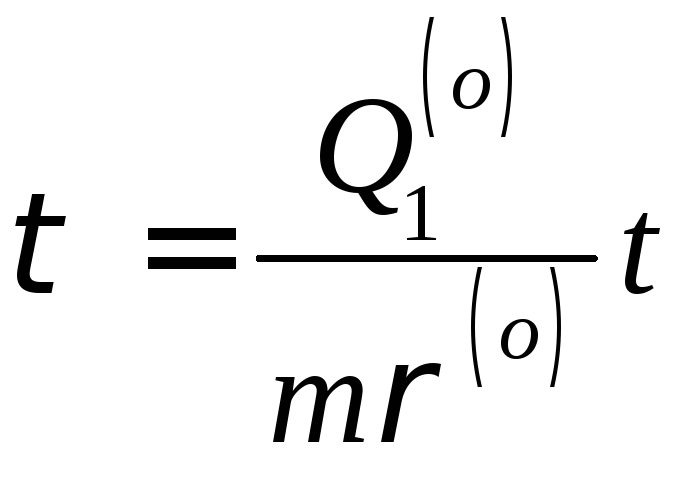
Асимптотика фактически соответствует тому, что мы "растягиваем" координату в окрестности ее начала. В этом можно убедиться, если произвести замену переменных

,.

В этом случае (8.2) сводится к уравнению

, которое упрощается, а исходная постановка сводится к классической задаче Баклея-Леверетта:

,,. (8.11)

Другими словами, мы рассматриваем возмущение в окрестности начала координат, где производные очень велики, и правой частью уравнения (8.2) можно пренебречь. Эта задача имеет известное решение, которое включает в себя сильный разрыв в точке . Он совпадает с характеристикой и движется с постоянной скоростью

, а)

.b) (8.12)

В области до разрыва решение имеет форму центрированной волны

. (8.13)

Подставляя (1.10) в (8.13) и разрешая относительно , получаем

или. (8.14)

Полученный результат позволяет построить область влияния для выколотой начальной точки, которая представляет собой участок центрированного решения задачи Коши. Действительно, характеристические уравнения для температуры включают в себя насыщенность. Поэтому температурная составляющая решения зависит от насыщенности и начальных параметров. Указанное дополнительное условие сводится к тому, что мы фиксируем насыщенность в этой точке и полагаем ее равной насыщенности уже после скачка на разрыве насыщенности. Формально это дополнительное условие сводится к видоизменению начального условия (8.6), которое можно представить в следующей форме

,,при,, а)

,,при,,b) (8.15)

,при,,. с) Здесь символыозначают, что граничное условие берется соответственно точно на границе и (соответственно) чуть отойдя от нее на малое расстояние. При этом насыщенность падает сразу до значения, равного, а температура – до значения, которое соответствует скачку температуры, связанному со скачком насыщенности. Два условия (8.15a,b) порождают два температурных скачка, которые движутся с разными скоростями. Значениеопределяется решением задачи, а точнее говоря – условием Гюгонио на разрыве.