
- •Preface
- •Part IV. Basic Single Equation Analysis
- •Chapter 18. Basic Regression Analysis
- •Equation Objects
- •Specifying an Equation in EViews
- •Estimating an Equation in EViews
- •Equation Output
- •Working with Equations
- •Estimation Problems
- •References
- •Chapter 19. Additional Regression Tools
- •Special Equation Expressions
- •Robust Standard Errors
- •Weighted Least Squares
- •Nonlinear Least Squares
- •Stepwise Least Squares Regression
- •References
- •Chapter 20. Instrumental Variables and GMM
- •Background
- •Two-stage Least Squares
- •Nonlinear Two-stage Least Squares
- •Limited Information Maximum Likelihood and K-Class Estimation
- •Generalized Method of Moments
- •IV Diagnostics and Tests
- •References
- •Chapter 21. Time Series Regression
- •Serial Correlation Theory
- •Testing for Serial Correlation
- •Estimating AR Models
- •ARIMA Theory
- •Estimating ARIMA Models
- •ARMA Equation Diagnostics
- •References
- •Chapter 22. Forecasting from an Equation
- •Forecasting from Equations in EViews
- •An Illustration
- •Forecast Basics
- •Forecasts with Lagged Dependent Variables
- •Forecasting with ARMA Errors
- •Forecasting from Equations with Expressions
- •Forecasting with Nonlinear and PDL Specifications
- •References
- •Chapter 23. Specification and Diagnostic Tests
- •Background
- •Coefficient Diagnostics
- •Residual Diagnostics
- •Stability Diagnostics
- •Applications
- •References
- •Part V. Advanced Single Equation Analysis
- •Chapter 24. ARCH and GARCH Estimation
- •Basic ARCH Specifications
- •Estimating ARCH Models in EViews
- •Working with ARCH Models
- •Additional ARCH Models
- •Examples
- •References
- •Chapter 25. Cointegrating Regression
- •Background
- •Estimating a Cointegrating Regression
- •Testing for Cointegration
- •Working with an Equation
- •References
- •Binary Dependent Variable Models
- •Ordered Dependent Variable Models
- •Censored Regression Models
- •Truncated Regression Models
- •Count Models
- •Technical Notes
- •References
- •Chapter 27. Generalized Linear Models
- •Overview
- •How to Estimate a GLM in EViews
- •Examples
- •Working with a GLM Equation
- •Technical Details
- •References
- •Chapter 28. Quantile Regression
- •Estimating Quantile Regression in EViews
- •Views and Procedures
- •Background
- •References
- •Chapter 29. The Log Likelihood (LogL) Object
- •Overview
- •Specification
- •Estimation
- •LogL Views
- •LogL Procs
- •Troubleshooting
- •Limitations
- •Examples
- •References
- •Part VI. Advanced Univariate Analysis
- •Chapter 30. Univariate Time Series Analysis
- •Unit Root Testing
- •Panel Unit Root Test
- •Variance Ratio Test
- •BDS Independence Test
- •References
- •Part VII. Multiple Equation Analysis
- •Chapter 31. System Estimation
- •Background
- •System Estimation Methods
- •How to Create and Specify a System
- •Working With Systems
- •Technical Discussion
- •References
- •Vector Autoregressions (VARs)
- •Estimating a VAR in EViews
- •VAR Estimation Output
- •Views and Procs of a VAR
- •Structural (Identified) VARs
- •Vector Error Correction (VEC) Models
- •A Note on Version Compatibility
- •References
- •Chapter 33. State Space Models and the Kalman Filter
- •Background
- •Specifying a State Space Model in EViews
- •Working with the State Space
- •Converting from Version 3 Sspace
- •Technical Discussion
- •References
- •Chapter 34. Models
- •Overview
- •An Example Model
- •Building a Model
- •Working with the Model Structure
- •Specifying Scenarios
- •Using Add Factors
- •Solving the Model
- •Working with the Model Data
- •References
- •Part VIII. Panel and Pooled Data
- •Chapter 35. Pooled Time Series, Cross-Section Data
- •The Pool Workfile
- •The Pool Object
- •Pooled Data
- •Setting up a Pool Workfile
- •Working with Pooled Data
- •Pooled Estimation
- •References
- •Chapter 36. Working with Panel Data
- •Structuring a Panel Workfile
- •Panel Workfile Display
- •Panel Workfile Information
- •Working with Panel Data
- •Basic Panel Analysis
- •References
- •Chapter 37. Panel Estimation
- •Estimating a Panel Equation
- •Panel Estimation Examples
- •Panel Equation Testing
- •Estimation Background
- •References
- •Part IX. Advanced Multivariate Analysis
- •Chapter 38. Cointegration Testing
- •Johansen Cointegration Test
- •Single-Equation Cointegration Tests
- •Panel Cointegration Testing
- •References
- •Chapter 39. Factor Analysis
- •Creating a Factor Object
- •Rotating Factors
- •Estimating Scores
- •Factor Views
- •Factor Procedures
- •Factor Data Members
- •An Example
- •Background
- •References
- •Appendix B. Estimation and Solution Options
- •Setting Estimation Options
- •Optimization Algorithms
- •Nonlinear Equation Solution Methods
- •References
- •Appendix C. Gradients and Derivatives
- •Gradients
- •Derivatives
- •References
- •Appendix D. Information Criteria
- •Definitions
- •Using Information Criteria as a Guide to Model Selection
- •References
- •Appendix E. Long-run Covariance Estimation
- •Technical Discussion
- •Kernel Function Properties
- •References
- •Index
- •Symbols
- •Numerics
654—Chapter 37. Panel Estimation
If, for example, you estimate an equation that uses orthogonal deviations to remove a crosssection fixed effect, EViews will, by default, compute orthogonal deviations of the instruments provided prior to their use. Thus, the instrument list:
z1 z2 @lev(z3)
will use the transformed Z1 and Z2, and the original Z3 as the instruments for the specification.
Note that in specifications where @dyn and @lev keywords are not relevant, they will be ignored. If, for example, you first estimate a GMM specification using first differences with both dynamic and level instruments, and then re-estimate the equation using LS, EViews will ignore the keywords, and use the instruments in their original forms.
GMM Options
Lastly, clicking on the Options tab in the dialog brings up a page displaying computational options for GMM estimation. These options are virtually identical to those for both LS and IV estimation (see “LS Options” on page 650). The one difference is in the option for saving estimation weights with the object. In the GMM context, this option applies to both the saving of GLS as well as GMM weights.
Panel Estimation Examples
Least Squares Examples
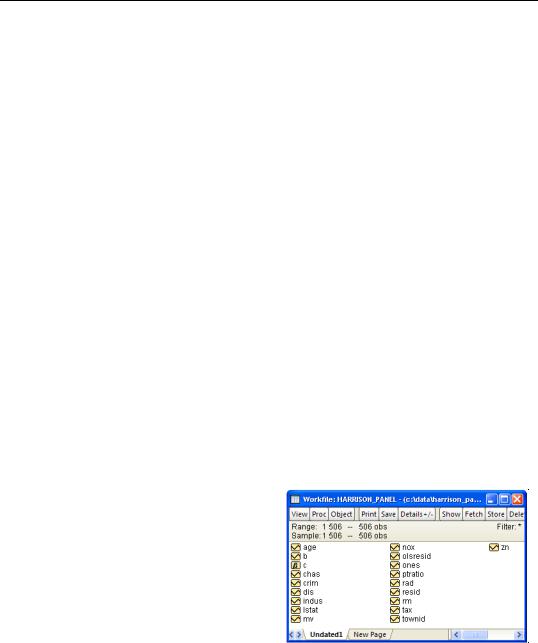
To illustrate the estimation of panel equations in EViews, we first consider an example involving unbalanced panel data from Harrison and Rubinfeld (1978) for the study of hedonic pricing (“Harrison_panel.WF1”). The data are well known and used as an example dataset in many sources (e.g., Baltagi (2005), p. 171).
The data consist of 506 census tract observations on 92 towns in the Boston area with group sizes ranging from 1 to 30. The dependent variable of interest is the logarithm of the median value of owner occupied houses (MV), and the regressors include various measures of housing desirability.
We begin our example by structuring our workfile as an undated panel. Click on the
“Range:” description in the workfile window, select Undated Panel, and enter “TOWNID” as the Identifier series. EViews will prompt you twice to create a CELLID series to uniquely identify observations. Click on OK to both questions to accept your settings.
Panel Estimation Examples—655
EViews restructures your workfile so that it is an unbalanced panel workfile. The top portion of the workfile window will change to show the
undated structure which has 92 cross-sections and a maximum of 30 observations in a cross-section.
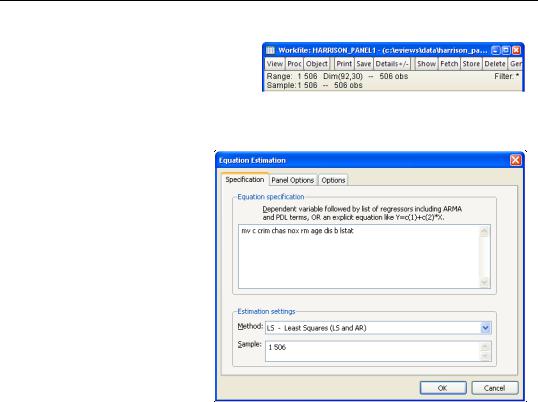
Next, we open the equation specification dialog by selecting Quick/Estimate Equation from the main EViews menu.
First, following Baltagi and Chang (1994) (also described in Baltagi, 2005), we estimate a fixed effects specification of a hedonic housing equation. The dependent variable in our specification is the median value MV, and the regressors are the crime rate (CRIM), a dummy variable for the property along
Charles River (CHAS), air pollution (NOX), average number of rooms (RM), proportion of older units (AGE), distance from employment centers (DIS), proportion of African-Ameri- cans in the population (B), and the proportion of lower status individuals (LSTAT). Note that you may include a constant term C in the specification. Since we are estimating a fixed effects specification, EViews will add one if it is not present so that the fixed effects estimates are relative to the constant term and add up to zero.
Click on the Panel Options tab and select Fixed for the Cross-section effects. To match the Baltagi and Chang results, we will leave the remaining settings at their defaults. Click on OK to accept the specification.

656—Chapter 37. Panel Estimation
Dependent Variable: MV
Method: Panel Least Squares
Date: 08/23/06 Time: 14:29
Sample: 1 506
Periods included: 30
Cross-sections included: 92
Total panel (unbalanced) observations: 506
|
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
C |
8.993272 |
0.134738 |
66.74632 |
0.0000 |
CRIM |
-0.625400 |
0.104012 |
-6.012746 |
0.0000 |
CHAS |
-0.452414 |
0.298531 |
-1.515467 |
0.1304 |
NOX |
-0.558938 |
0.135011 |
-4.139949 |
0.0000 |
RM |
0.927201 |
0.122470 |
7.570833 |
0.0000 |
AGE |
-1.406955 |
0.486034 |
-2.894767 |
0.0040 |
DIS |
0.801437 |
0.711727 |
1.126045 |
0.2608 |
B |
0.663405 |
0.103222 |
6.426958 |
0.0000 |
LSTAT |
-2.453027 |
0.255633 |
-9.595892 |
0.0000 |
|
|
|
|
|
|
|
|
|
|
Effects Specification
Cross-section fixed (dummy variables)
R-squared |
0.918370 |
Mean dependent var |
9.942268 |
Adjusted R-squared |
0.898465 |
S.D. dependent var |
0.408758 |
S.E. of regression |
0.130249 |
Akaike info criterion |
-1.063668 |
Sum squared resid |
6.887683 |
Schwarz criterion |
-0.228384 |
Log likelihood |
369.1080 |
Hannan-Quinn criter. |
-0.736071 |
F-statistic |
46.13805 |
Durbin-Watson stat |
1.999986 |
Prob(F-statistic) |
0.000000 |
|
|
|
|
|
|
|
|
|
|
The results for the fixed effects estimation are depicted here. Note that as in pooled estimation, the reported R-squared and F-statistics are based on the difference between the residuals sums of squares from the estimated model, and the sums of squares from a single constant-only specification, not from a fixed-effect-only specification. Similarly, the reported information criteria report likelihoods adjusted for the number of estimated coefficients, including fixed effects. Lastly, the reported Durbin-Watson stat is formed simply by computing the first-order residual correlation on the stacked set of residuals.
We may click on the Estimate button to modify the specification to match the Wallace-Hus- sain random effects specification considered by Baltagi and Chang. We modify the specification to include the additional regressors (ZN, INDUS, RAD, TAX, PTRATIO) used in estimation, change the cross-section effects to be estimated as a random effect, and use the Options page to set the random effects computation method to Wallace-Hussain.
The top portion of the resulting output is given by:
Panel Estimation Examples—657
Dependent Variable: MV
Method: Panel EGLS (Cross-section random effects)
Date: 08/23/06 Time: 14:34
Sample: 1 506
Periods included: 30
Cross-sections included: 92
Total panel (unbalanced) observations: 506
Wallace and Hussain estimator of component variances
|
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
C |
9.684427 |
0.207691 |
46.62904 |
0.0000 |
CRIM |
-0.737616 |
0.108966 |
-6.769233 |
0.0000 |
ZN |
0.072190 |
0.684633 |
0.105443 |
0.9161 |
INDUS |
0.164948 |
0.426376 |
0.386860 |
0.6990 |
CHAS |
-0.056459 |
0.304025 |
-0.185703 |
0.8528 |
NOX |
-0.584667 |
0.129825 |
-4.503496 |
0.0000 |
RM |
0.908064 |
0.123724 |
7.339410 |
0.0000 |
AGE |
-0.871415 |
0.487161 |
-1.788760 |
0.0743 |
DIS |
-1.423611 |
0.462761 |
-3.076343 |
0.0022 |
RAD |
0.961362 |
0.280649 |
3.425493 |
0.0007 |
TAX |
-0.376874 |
0.186695 |
-2.018658 |
0.0441 |
PTRATIO |
-2.951420 |
0.958355 |
-3.079674 |
0.0022 |
B |
0.565195 |
0.106121 |
5.325958 |
0.0000 |
LSTAT |
-2.899084 |
0.249300 |
-11.62891 |
0.0000 |
|
|
|
|
|
|
|
|
|
|
|
Effects Specification |
|
|
|
|
|
|
S.D. |
Rho |
|
|
|
|
|
|
|
|
|
|
Cross-section random |
|
|
0.126983 |
0.4496 |
Idiosyncratic random |
|
|
0.140499 |
0.5504 |
|
|
|
|
|
|
|
|
|
|
Note that the estimates of the component standard deviations must be squared to match the component variances reported by Baltagi and Chang (0.016 and 0.020, respectively).
Next, we consider an example of estimation with standard errors that are robust to serial correlation. For this example, we employ data on job training grants (“Jtrain.WF1”) used in examples from Wooldridge (2002, p. 276 and 282).
As before, the first step is to structure the workfile as a panel workfile. Click
658—Chapter 37. Panel Estimation
on Range: to bring up the dialog, and enter “YEAR” as the date identifier and “FCODE” as the cross-section ID.
EViews will structure the workfile so that it is a panel workfile with 157 cross-sections, and three annual observations. Note that even though there
are 471 observations in the workfile, a large number of them contain missing values for variables of interest.
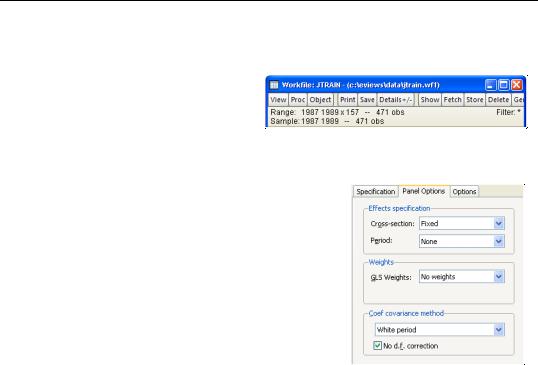
To estimate the fixed effect specification with robust standard errors (Wooldridge example 10.5, p. 276), click on specification Quick/Estimate Equation from the main EViews menu. Enter the list specification:
lscrap c d88 d89 grant grant_1
in the Equation specification edit box on the main page and select Fixed in the Cross-section effects specification combo box on the Panel Options page. Lastly, since we wish to compute standard errors that are robust to serial correlation (Arellano (1987), White (1980)), we choose White period as the Coef covari-
ance method. To match the reported Wooldridge example, we must select No d.f. correction in the covariance calculation. Click on OK to accept the options. EViews displays the results from estimation:

Panel Estimation Examples—659
Dependent Variable: LSCRAP
Method: Panel Least Squares
Date: 08/18/09 Time: 12:03
Sample: 1987 1989
Periods included: 3
Cross-sections included: 54
Total panel (balanced) observations: 162
White period standard errors & covariance (no d.f. correction)
WARNING: estimated coefficient covariance matrix is of reduced rank
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
C |
0.597434 |
0.062489 |
9.560565 |
0.0000 |
D88 |
-0.080216 |
0.095719 |
-0.838033 |
0.4039 |
D89 |
-0.247203 |
0.192514 |
-1.284075 |
0.2020 |
GRANT |
-0.252315 |
0.140329 |
-1.798022 |
0.0751 |
GRANT_1 |
-0.421589 |
0.276335 |
-1.525648 |
0.1301 |
|
|
|
|
|
|
|
|
|
|
Effects Specification
Cross-section fixed (dummy variables)
R-squared |
0.927572 |
Mean dependent var |
0.393681 |
Adjusted R-squared |
0.887876 |
S.D. dependent var |
1.486471 |
S.E. of regression |
0.497744 |
Akaike info criterion |
1.715383 |
Sum squared resid |
25.76593 |
Schwarz criterion |
2.820819 |
Log likelihood |
-80.94602 |
Hannan-Quinn criter. |
2.164207 |
F-statistic |
23.36680 |
Durbin-Watson stat |
1.996983 |
Prob(F-statistic) |
0.000000 |
|
|
|
|
|
|
|
|
|
|
Note that EViews automatically adjusts for the missing values in the data. There are only 162 observations on 54 cross-sections used in estimation. The top portion of the output indicates that the results use robust White period standard errors with no d.f. correction. Notice that EViews warns you that the estimated coefficient covariances is not of full rank.
Alternately, we may estimate a first difference estimator for these data with robust standard errors (Wooldridge example 10.6, p. 282). Open a new equation dialog by clicking on Quick/Estimate Equation..., or modify the existing equation by clicking on the Estimate button on the equation toolbar. Enter the specification:
d(lscrap) c d89 d(grant) d(grant_1)
in the Equation specification edit box on the main page, select None in the Cross-section effects specification combo box, White period and No d.f. correction for the coefficient covariance method on the Panel Options page. The results are given by:

660—Chapter 37. Panel Estimation
Dependent Variable: D(LSCRAP)
Method: Panel Least Squares
Date: 08/18/09 Time: 12:05
Sample (adjusted): 1988 1989
Periods included: 2
Cross-sections included: 54
Total panel (balanced) observations: 108
White period standard errors & covariance (no d.f. correction)
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
C |
-0.090607 |
0.088082 |
-1.028671 |
0.3060 |
D89 |
-0.096208 |
0.111002 |
-0.866721 |
0.3881 |
D(GRANT) |
-0.222781 |
0.128580 |
-1.732624 |
0.0861 |
D(GRANT_1) |
-0.351246 |
0.264662 |
-1.327147 |
0.1874 |
|
|
|
|
|
R-squared |
0.036518 |
Mean dependent var |
-0.221132 |
|
Adjusted R-squared |
0.008725 |
S.D. dependent var |
0.579248 |
|
S.E. of regression |
0.576716 |
Akaike info criterion |
1.773399 |
|
Sum squared resid |
34.59049 |
Schwarz criterion |
1.872737 |
|
Log likelihood |
-91.76352 |
Hannan-Quinn criter. |
1.813677 |
|
F-statistic |
1.313929 |
Durbin-Watson stat |
1.498132 |
|
Prob(F-statistic) |
0.273884 |
|
|
|
|
|
|
|
|
|
|
|
|
|
While current versions of EViews do not provide a full set of specification tests for panel equations, it is a straightforward task to construct some tests using residuals obtained from the panel estimation.
To continue with the Wooldridge example, we may test for AR(1) serial correlation in the first-differenced equation by regressing the residuals from this specification on the lagged residuals using data for the year 1989. First, we save the residual series in the workfile.
Click on Proc/Make Residual Series... on the estimated equation toolbar, and save the residuals to the series RESID01.
Next, regress RESID01 on RESID01(-1), yielding:

Panel Estimation Examples—661
Dependent Variable: RESID01
Method: Panel Least Squares
Date: 08/18/09 Time: 12:11
Sample (adjusted): 1989 1989
Periods included: 1
Cross-sections included: 54
Total panel (balanced) observations: 54
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
RESID01(-1) |
0.236906 |
0.133357 |
1.776481 |
0.0814 |
|
|
|
|
|
|
|
|
|
|
R-squared |
0.056199 |
Mean dependent var |
6.17E-18 |
|
Adjusted R-squared |
0.056199 |
S.D. dependent var |
0.571061 |
|
S.E. of regression |
0.554782 |
Akaike info criterion |
1.677863 |
|
Sum squared resid |
16.31252 |
Schwarz criterion |
1.714696 |
|
Log likelihood |
-44.30230 |
Hannan-Quinn criter. |
1.692068 |
|
Durbin-Watson stat |
0.000000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Under the null hypothesis that the original idiosyncratic errors are uncorrelated, the residu-
als from this equation should have an autocorrelation coefficient of -0.5. Here, we obtain an estimate of rˆ 1 = 0.237 which appears to be far from the null value. A formal Wald
hypothesis test rejects the null that the original idiosyncratic errors are serially uncorrelated. Perform a Wald test on the test equation by clicking on View/Coefficient Diagnostics/ Wald-Coefficient Restrictions... and entering the restriction “C(1)=-0.5” in the edit box:
Wald Test:
Equation: Untitled
Null Hypothesis: C(1)=-0.5
Test Statistic |
Value |
df |
Probability |
|
|
|
|
|
|
|
|
t-statistic |
5.525812 |
53 |
0.0000 |
F-statistic |
30.53460 |
(1, 53) |
0.0000 |
Chi-square |
30.53460 |
1 |
0.0000 |
|
|
|
|
|
|
|
|
Null Hypothesis Summary: |
|
|
|
|
|
|
|
|
|
|
|
Normalized Restriction (= 0) |
Value |
Std. Err. |
|
|
|
|
|
|
|
|
|
0.5 + C(1) |
|
0.736906 |
0.133357 |
|
|
|
|
|
|
|
|
Restrictions are linear in coefficients.
The formal test confirms our casual observation, strongly rejecting the null hypothesis.
Instrumental Variables Example
To illustrate the estimation of instrumental variables panel estimators, we consider an example taken from Papke (1994) for enterprise zone data for 22 communities in Indiana that is outlined in Wooldridge (2002, p. 306).
662—Chapter 37. Panel Estimation
The panel workfile for this example is structured using YEAR as the period identifier, and CITY as the cross-section identifier. The result is a balanced annual panel for dates from 1980 to 1988 for 22 cross-sections.
To estimate the example specification, create a new equation by entering the keyword tsls in the command line, or by clicking on Quick/Estimate Equation... in the main menu. Selecting TSLS
- Two-Stage Least Squares (and AR) in the Method combo box to display the instrumental variables estimator dialog, if necessary, and enter:
d(luclms) c d(luclms(-1)) d(ez)
to regress the difference of log unemployment claims (LUCLMS) on the lag difference, and the difference of enterprise zone designation (EZ). Since the model is estimated with time intercepts, you should click on the Panel Options page, and select Fixed for the Period effects.
Next, click on the Instruments tab, and add the names:
c d(luclms(-2)) d(ez)
to the Instrument list edit box. Note that adding the constant C to the regressor and instrument boxes is not required since the fixed effects estimator will add it for you. Click on OK to accept the dialog settings. EViews displays the output for the IV regression:

Panel Estimation Examples—663
Dependent Variable: D(LUCLMS)
Method: Panel Two-Stage Least Squares
Date: 08/23/06 Time: 15:52
Sample (adjusted): 1983 1988
Periods included: 6
Cross-sections included: 22
Total panel (balanced) observations: 132
Instrument list: C D(LUCLMS(-2)) D(EZ)
|
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
C |
-0.201654 |
0.040473 |
-4.982442 |
0.0000 |
D(LUCLMS(-1)) |
0.164699 |
0.288444 |
0.570992 |
0.5690 |
D(EZ) |
-0.218702 |
0.106141 |
-2.060493 |
0.0414 |
|
|
|
|
|
|
|
|
|
|
|
Effects Specification |
|
|
|
|
|
|
|
|
|
|
|
|
|
Period fixed (dummy variables) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R-squared |
0.280533 |
Mean dependent var |
-0.235098 |
|
Adjusted R-squared |
0.239918 |
S.D. dependent var |
0.267204 |
|
S.E. of regression |
0.232956 |
Sum squared resid |
6.729300 |
|
F-statistic |
9.223709 |
Durbin-Watson stat |
2.857769 |
|
Prob(F-statistic) |
0.000000 |
Second-Stage SSR |
6.150596 |
|
Instrument rank |
8.000000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Note that the instrument rank in this equation is 8 since the period dummies also serve as instruments, so you have the 3 instruments specified explicitly, plus 5 for the non-collinear period dummy variables.
GMM Example
To illustrate the estimation of dynamic panel data models using GMM, we employ the unbalanced 1031 observation panel of firm level data (“Abond_pan.WF1”) from Layard and Nickell (1986), previously examined by Arellano and Bond (1991). The analysis fits the log of employment (N) to the log of the real wage (W), log of the capital stock (K), and the log of industry output (YS).
664—Chapter 37. Panel Estimation
The workfile is structured as a dated annual panel using ID as the cross-section identifier series and YEAR as the date classification series.
Since the model is assumed to be dynamic, we employ EViews tools for estimating dynamic panel data models. To bring up the GMM dialog, enter the keyword gmm in the command line, or select Quick/Estimate Equation... from the main menu, and choose
GMM/DPD - Generalized Method of Moments / Dynamic Panel Data in the Method combo box to display the IV estimator dialog.
Click on the button labeled Dynamic Panel Wizard... to bring up the DPD wizard. The DPD wizard is a tool that will aid you in filling out the general GMM dialog. The first page is an introductory screen describing the basic purpose of the wizard. Click Next to continue.
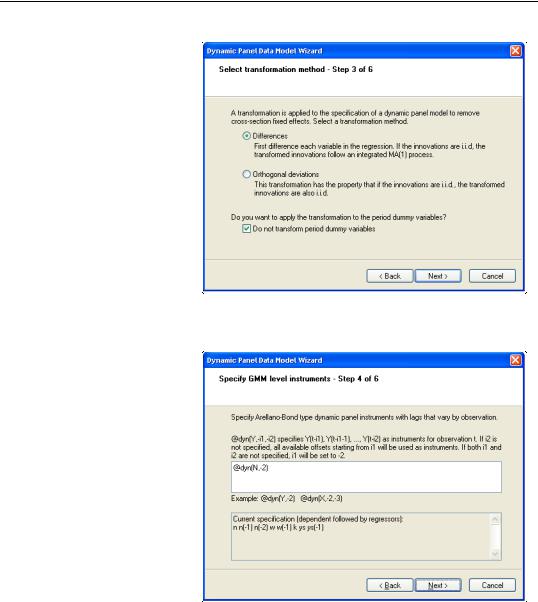
The second page of the wizard prompts you for the dependent variable and the number of its lags to include as explanatory variables. In this example, we wish to estimate an equation with N as the dependent variable and N(-1) and N(-2) as explanatory variables so we enter “N” and select “2” lags in the combo box. Click on Next to continue to the next page, where you will specify the remaining explanatory variables.
In the next page, you will complete the specification of your explanatory variables. First, enter the list:
w w(-1) k ys ys(-1)
in the regressor edit box to include these variables. Since the desired specification will include time dummies, make certain that the checkbox for Include period dummy variables is selected, then click on Next to proceed.
Panel Estimation Examples—665
The next page of the wizard is used to specify a transformation to remove the cross-section fixed effect. You may choose to use first Differences or Orthogonal deviations. In addition, if your specification includes period dummy variables, there is a checkbox asking whether you wish to transform the period dummies, or to enter them in levels. Here we specify the first difference transformation,
and choose to include untransformed period dummies in the transformed equation. Click on Next to continue.
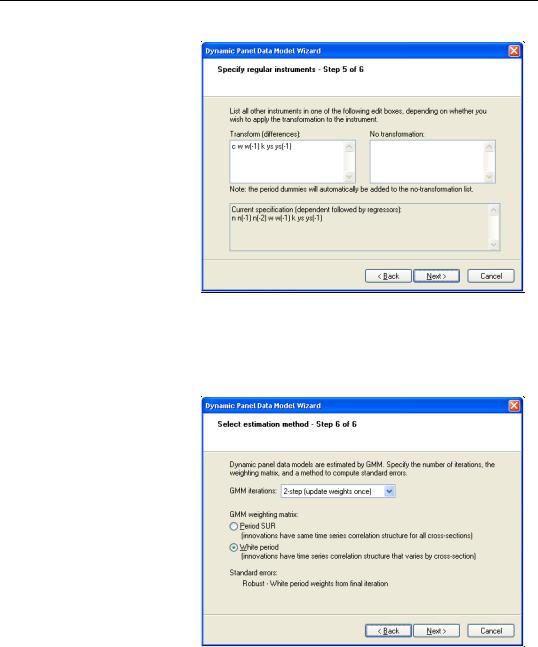
The next page is where you will specify your dynamic period-specific (predetermined) instruments. The instruments should be entered with the “@DYN” tag to indicate that they are to be expanded into sets of predetermined instruments, with optional arguments to indicate the lags to be included. If no arguments are provided, the default is to include all valid lags (from -2 to “-infinity”).
Here, we instruct EViews that we wish to use the default lags for N as predetermined instruments.
666—Chapter 37. Panel Estimation
You should now specify the remaining instruments. There are two lists that should be provided. The first list, which is entered in the edit field labeled Transform, should contain a list of the strictly exogenous instruments that you wish to transform prior to use in estimating the transformed equation. The second list, which should be entered in the
No transform edit box should contain a list of
instruments that should be used directly without transformation. Enter the remaining instruments:
w w(-1) k ys ys(-1)
in the first edit box and click on Next to proceed to the final page.
The final page allows you to specify your GMM weighting and coefficient covariance calculation choices. In the first combo box, you will choose a GMM Iteration option. You may select 1-step (for i.i.d. innovations) to compute the Arellano-Bond 1- step estimator, 2-step (update weights once), to compute the ArellanoBond 2-step estimator, or n-step (iterate to convergence), to iterate the
weight calculations. In the first case, EViews will provide you with choices for computing the standard errors, but here only White period robust standard errors are allowed. Clicking on Next takes you to the final page. Click on Finish to return to the Equation Estimation dialog.

Panel Estimation Examples—667
EViews has filled out the Equation Estimation dialog with our choices from the DPD wizard. You should take a moment to examine the settings that have been filled out for you since, in the future, you may wish to enter the specification directly into the dialog without using the wizard. You may also, of course, modify the settings in the dialog prior to continuing. For example, click on the Panel Options tab and check the No d.f. correction setting in the covariance calculation to match the original Arellano-Bond results (Table 4(b), p. 290). Click on OK to estimate the specification.
The top portion of the output describes the estimation settings, coefficient estimates, and summary statistics. Note that both the weighting matrix and covariance calculation method used are described in the top portion of the output.
Dependent Variable: N
Method: Panel Generalized Method of Moments Transformation: First Differences
Date: 08/24/06 Time: 14:21
Sample (adjusted): 1979 1984 Periods included: 6 Cross-sections included: 140
Total panel (unbalanced) observations: 611 White period instrument weighting matrix
White period standard errors & covariance (no d.f. correction) Instrument list: @DYN(N, -2) W W(-1) K YS YS(-1)
@LEV(@SYSPER)
|
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
N(-1) |
0.474150 |
0.088714 |
5.344699 |
0.0000 |
N(-2) |
-0.052968 |
0.026721 |
-1.982222 |
0.0479 |
W |
-0.513205 |
0.057323 |
-8.952838 |
0.0000 |
W(-1) |
0.224640 |
0.080614 |
2.786626 |
0.0055 |
K |
0.292723 |
0.042243 |
6.929542 |
0.0000 |
YS |
0.609775 |
0.111029 |
5.492054 |
0.0000 |
YS(-1) |
-0.446371 |
0.125598 |
-3.553963 |
0.0004 |
@LEV(@ISPERIOD("1979")) |
0.010509 |
0.006831 |
1.538482 |
0.1245 |
@LEV(@ISPERIOD("1980")) |
0.014142 |
0.009924 |
1.425025 |
0.1547 |
@LEV(@ISPERIOD("1981")) |
-0.040453 |
0.012197 |
-3.316629 |
0.0010 |
@LEV(@ISPERIOD("1982")) |
-0.021640 |
0.011353 |
-1.906127 |
0.0571 |
@LEV(@ISPERIOD("1983")) |
-0.001847 |
0.010807 |
-0.170874 |
0.8644 |
@LEV(@ISPERIOD("1984")) |
-0.010221 |
0.010548 |
-0.968937 |
0.3330 |
|
|
|
|
|
|
|
|
|
|
The standard errors that we report here are the standard Arellano-Bond 2-step estimator standard errors. Note that there is evidence in the literature that the standard errors for the two-step estimator may not be reliable.
The bottom portion of the output displays additional information about the specification and summary statistics:
