32—Chapter 19. Additional Regression Tools

Dependent Variable: LPRICE

Method: Least Squares

Date: 08/08/09 Time: 22:15

Sample: 1 506

Included observations: 506

Robust Standard Errors

In the standard least squares model, the coefficient variance-covariance matrix may be derived as:

A key part of this derivation is the assumption that the error terms, e , are conditionally homoskedastic, which implies that Q = E(X¢ee¢X § T) = j2(X¢X § T) . A sufficient, but not necessary, condition for this restriction is that the errors are i.i.d. In cases where this assumption is relaxed to allow for heteroskedasticity or autocorrelation, the expression for the covariance matrix will be different.

EViews provides built-in tools for estimating the coefficient covariance under the assumption that the residuals are conditionally heteroskedastic, and under the assumption of heteroskedasticity and autocorrelation. The coefficient covariance estimator under the first assumption is termed a Heteroskedasticity Consistent Covariance (White) estimator, and the

34—Chapter 19. Additional Regression Tools

Dependent Variable: LOG(WAGE)

Method: Least Squares

Date: 04/13/09 Time: 16:56

Sample: 1 526

Included observations: 526

White heteroskedasticity-consistent standard errors & covariance

As Wooldridge notes, the heteroskedasticity robust standard errors for this specification are not very different from the non-robust forms, and the test statistics for statistical significance of coefficients are generally unchanged. While robust standard errors are often larger than their usual counterparts, this is not necessarily the case, and indeed this equation has some robust standard errors that are smaller than the conventional estimates.

HAC Consistent Covariances (Newey-West)

The White covariance matrix described above assumes that the residuals of the estimated equation are serially uncorrelated. Newey and West (1987b) have proposed a more general covariance estimator that is consistent in the presence of both heteroskedasticity and autocorrelation of unknown form. They propose using HAC methods to form an estimate of

E(X¢ee¢X § T). Then the HAC coefficient covariance estimator is given by:

where ˆ is any of the LRCOV estimators described in Appendix E. “Long-run Covariance

Q

Estimation,” on page 775.

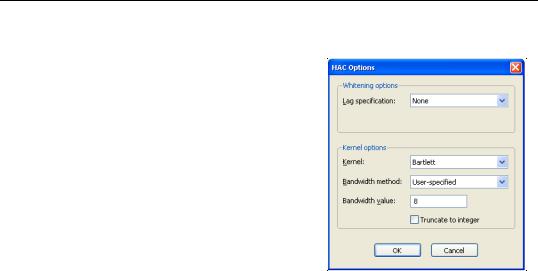
To use the Newey-West HAC method, select the Options tab and select HAC (Newey-West) in the Coefficient covariance matrix drop-down. As before, you may use the checkbox to remove the default d.f. Adjustment.