This chapter describes methods of estimating the parameters of systems of equations. We describe least squares, weighted least squares, seemingly unrelated regression (SUR), weighted two-stage least squares, three-stage least squares, full-information maximum likelihood (FIML), generalized method of moments (GMM), and autoregressive conditional heteroskedasticity (ARCH) estimation techniques.
Once you have estimated the parameters of your system of equations, you may wish to forecast future values or perform simulations for different values of the explanatory variables. Chapter 34. “Models,” on page 511 describes the use of models to forecast from an estimated system of equations or to perform single and multivariate simulation.
Background
A system is a group of equations containing unknown parameters. Systems can be estimated using a number of multivariate techniques that take into account the interdependencies among the equations in the system.
The general form of a system is:
f(yt, xt, b) = et ,
(31.1)
where yt is a vector of endogenous variables, xt is a vector of exogenous variables, and et is a vector of possibly serially correlated disturbances. The task of estimation is to find estimates of the vector of parameters b .
EViews provides you with a number of methods of estimating the parameters of the system. One approach is to estimate each equation in the system separately, using one of the single equation methods described earlier in this manual. A second approach is to estimate, simultaneously, the complete set of parameters of the equations in the system. The simultaneous approach allows you to place constraints on coefficients across equations and to employ techniques that account for correlation in the residuals across equations.
While there are important advantages to using a system to estimate your parameters, they do not come without cost. Most importantly, if you misspecify one of the equations in the system and estimate your parameters using single equation methods, only the misspecified equation will be poorly estimated. If you employ system estimation techniques, the poor estimates for the misspecification equation may “contaminate” estimates for other equations.
At this point, we take care to distinguish between systems of equations and models. A model is a group of known equations describing endogenous variables. Models are used to
420—Chapter 31. System Estimation
solve for values of the endogenous variables, given information on other variables in the model.
Systems and models often work together quite closely. You might estimate the parameters of a system of equations, and then create a model in order to forecast or simulate values of the endogenous variables in the system. We discuss this process in greater detail in Chapter 34. “Models,” on page 511.
System Estimation Methods
EViews will estimate the parameters of a system of equations using:
The equations in the system may be linear or nonlinear, and may contain autoregressive error terms.
In the remainder of this section, we describe each technique at a general level. Users who are interested in the technical details are referred to the “Technical Discussion” on
page 446.
Ordinary Least Squares
This technique minimizes the sum-of-squared residuals for each equation, accounting for any cross-equation restrictions on the parameters of the system. If there are no such restrictions, this method is identical to estimating each equation using single-equation ordinary least squares.
Cross-Equation Weighting
This method accounts for cross-equation heteroskedasticity by minimizing the weighted sum-of-squared residuals. The equation weights are the inverses of the estimated equation variances, and are derived from unweighted estimation of the parameters of the system.
System Estimation Methods—421
This method yields identical results to unweighted single-equation least squares if there are no cross-equation restrictions.
Seemingly Unrelated Regression
The seemingly unrelated regression (SUR) method, also known as the multivariate regression, or Zellner's method, estimates the parameters of the system, accounting for heteroskedasticity and contemporaneous correlation in the errors across equations. The estimates of the cross-equation covariance matrix are based upon parameter estimates of the unweighted system.
Note that EViews estimates a more general form of SUR than is typically described in the literature, since it allows for cross-equation restrictions on parameters.
Two-Stage Least Squares
The system two-stage least squares (STSLS) estimator is the system version of the single equation two-stage least squares estimator described above. STSLS is an appropriate technique when some of the right-hand side variables are correlated with the error terms, and there is neither heteroskedasticity, nor contemporaneous correlation in the residuals. EViews estimates STSLS by applying TSLS equation by equation to the unweighted system, enforcing any cross-equation parameter restrictions. If there are no cross-equation restrictions, the results will be identical to unweighted single-equation TSLS.
Weighted Two-Stage Least Squares
The weighted two-stage least squares (WTSLS) estimator is the two-stage version of the weighted least squares estimator. WTSLS is an appropriate technique when some of the right-hand side variables are correlated with the error terms, and there is heteroskedasticity, but no contemporaneous correlation in the residuals.
EViews first applies STSLS to the unweighted system. The results from this estimation are used to form the equation weights, based upon the estimated equation variances. If there are no cross-equation restrictions, these first-stage results will be identical to unweighted single-equation TSLS.
Three-Stage Least Squares
Three-stage least squares (3SLS) is the two-stage least squares version of the SUR method. It is an appropriate technique when right-hand side variables are correlated with the error terms, and there is both heteroskedasticity, and contemporaneous correlation in the residuals.
EViews applies TSLS to the unweighted system, enforcing any cross-equation parameter restrictions. These estimates are used to form an estimate of the full cross-equation covari-
422—Chapter 31. System Estimation
ance matrix which, in turn, is used to transform the equations to eliminate the cross-equa- tion correlation. TSLS is applied to the transformed model.
Full Information Maximum Likelihood (FIML)
Full Information Maximum Likelihood (FIML) estimates the likelihood function under the assumption that the contemporaneous errors have a joint normal distribution. Provided that the likelihood function is correctly specified, FIML is fully efficient.
Generalized Method of Moments (GMM)
The GMM estimator belongs to a class of estimators known as M-estimators that are defined by minimizing some criterion function. GMM is a robust estimator in that it does not require information of the exact distribution of the disturbances.
GMM estimation is based upon the assumption that the disturbances in the equations are uncorrelated with a set of instrumental variables. The GMM estimator selects parameter estimates so that the correlations between the instruments and disturbances are as close to zero as possible, as defined by a criterion function. By choosing the weighting matrix in the criterion function appropriately, GMM can be made robust to heteroskedasticity and/or autocorrelation of unknown form.
Many standard estimators, including all of the system estimators provided in EViews, can be set up as special cases of GMM. For example, the ordinary least squares estimator can be viewed as a GMM estimator, based upon the conditions that each of the right-hand side variables is uncorrelated with the residual.
The System ARCH estimator is the multivariate version of ARCH estimator. System ARCH is an appropriate technique when one wants to model the variance and covariance of the error terms, generally in an autoregressive form. System ARCH allows you to choose from the most popular multivariate ARCH specifications: Constant Conditional Correlation, the Diagonal VECH, and (indirectly) the Diagonal BEKK.
How to Create and Specify a System
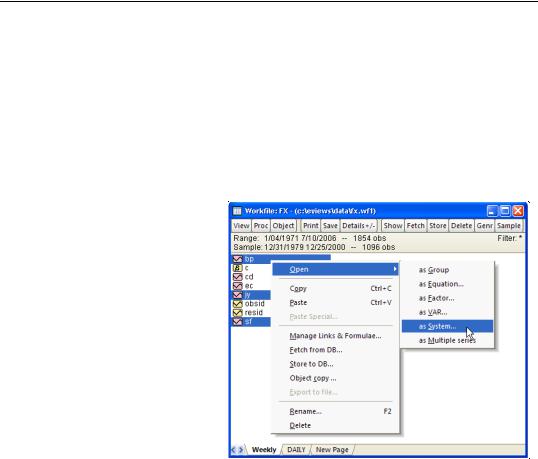
To estimate the parameters of your system of equations, you should first create a system object and specify the system of equations. There are three ways to specify the system: manually by entering a specification, by inserting a text file containing the specification, or by letting EViews create a system automatically from a selected list of variables,
To create a new system manually or by inserting a text file, click on Object/New Object.../ System or type system in the command window. A blank system object window should appear. You will fill the system specification window with text describing the equations, and potentially, lines describing the instruments and the parameter starting values. You
How to Create and Specify a System—423
may enter the text by typing in the specification, or clicking on the InsertTxt button and loading a specification from a text file. You may also insert a text file using the right-mouse button menu and selecting Insert Text File...
To estimate the parameters of your system of equations, you should first create a system object and specify the system of equations. Click on Object/New Object.../System or type system in the command window. The system object window should appear. When you first create the system, the window will be blank. You will fill the system specification window with text describing the equations, and potentially, lines describing the instruments and the parameter starting values.
From a list of selected variables, EViews can also automatically generate linear equations in a system. To use this procedure, first highlight the dependent variables that will be in the system. Next, double click on any of the highlighted series, and select Open/ Open System..., or right click and select Open/as System....
The Make System dialog box should appear with the variable names entered in the Dependent variables field. You can augment the specification by adding regressors or AR terms,
either estimated with common or equation specific coefficients. See “System Procs” on page 435 for additional details on this dialog.
The Make System proc is also available from a Group object (see “Make System,” on page 430).
Equations
Enter your equations, by formula, using standard EViews expressions. The equations in your system should be behavioral equations with unknown coefficients and an implicit error term.
424—Chapter 31. System Estimation
Consider the specification of a simple two equation system. You can use the default EViews coefficients, C(1), C(2), and so on, or you can use other coefficient vectors, in which case you should first declare them by clicking Object/New Object.../Matrix-Vec-tor-Coef/Coefficient Vector in the main menu.
There are some general rules for specifying your equations:
•Equations can be nonlinear in their variables, coefficients, or both. Cross equation coefficient restrictions may be imposed by using the same coefficients in different equations. For example:
y = c(1) + c(2)*x
z= c(3) + c(2)*z + (1-c(2))*x
•You may also impose adding up constraints. Suppose for the equation:
y= c(1)*x1 + c(2)*x2 + c(3)*x3
you wish to impose C(1)+C(2)+C(3)=1. You can impose this restriction by specifying the equation as:
y= c(1)*x1 + c(2)*x2 + (1-c(1)-c(2))*x3
•The equations in a system may contain autoregressive (AR) error specifications, but not MA, SAR, or SMA error specifications. You must associate coefficients with each AR specification. Enclose the entire AR specification in square brackets and follow each AR with an “=”-sign and a coefficient. For example:
cs = c(1) + c(2)*gdp + [ar(1)=c(3), ar(2)=c(4)]
You can constrain all of the equations in a system to have the same AR coefficient by giving all equations the same AR coefficient number, or you can estimate separate AR processes, by assigning each equation its own coefficient.
•Equations in a system need not have a dependent variable followed by an equal sign and then an expression. The “=”-sign can be anywhere in the formula, as in:
log(unemp/(1-unemp)) = c(1) + c(2)*dmr
You can also write the equation as a simple expression without a dependent variable, as in:
(c(1)*x + c(2)*y + 4)^2
When encountering an expression that does not contain an equal sign, EViews sets the entire expression equal to the implicit error term.
How to Create and Specify a System—425
If an equation should not have a disturbance, it is an identity, and should not be included in a system. If necessary, you should solve out for any identities to obtain the behavioral equations.
You should make certain that there is no identity linking all of the disturbances in your system. For example, if each of your equations describes a fraction of a total, the sum of the equations will always equal one, and the sum of the disturbances will identically equal zero. You will need to drop one of these equations to avoid numerical problems.
Instruments
If you plan to estimate your system using two-stage least squares, three-stage least squares, or GMM, you must specify the instrumental variables to be used in estimation. There are several ways to specify your instruments, with the appropriate form depending on whether you wish to have identical instruments in each equation, and whether you wish to compute the projections on an equation-by-equation basis, or whether you wish to compute a restricted projection using the stacked system.
In the simplest (default) case, EViews will form your instrumental variable projections on an equation-by-equation basis. If you prefer to think of this process as a two-step (2SLS) procedure, the first-stage regression of the variables in your model on the instruments will be run separately for each equation.
In this setting, there are two ways to specify your instruments. If you would like to use identical instruments in every equations, you should include a line beginning with the keyword “@INST” or “INST”, followed by a list of all the exogenous variables to be used as instruments. For example, the line:
@inst gdp(-1 to -4) x gov
instructs EViews to use these six variables as instruments for all of the equations in the system. System estimation will involve a separate projection for each equation in your system.
You may also specify different instruments for each equation by appending an “@”-sign at the end of the equation, followed by a list of instruments for that equation. For example:
The first equation uses CS(-1), INV(-1), GOV, and a constant as instruments, while the second equation uses GDP(-1), GOV, and a constant as instruments.
Lastly, you can mix the two methods. Any equation without individually specified instruments will use the instruments specified by the @inst statement. The system:
@inst gdp(-1 to -4) x gov
cs = c(1)+c(2)*gdp+c(3)*cs(-1)
426—Chapter 31. System Estimation
inv = c(4)+c(5)*gdp+c(6)*gov @ gdp(-1) gov
will use the instruments GDP(-1), GDP(-2), GDP(-3), GDP(-4), X, GOV, and C, for the CS equation, but only GDP(-1), GOV, and C, for the INV equation.
As noted above, the EViews default behavior is to perform the instrumental variables projection on an equation-by-equation basis. You may, however, wish to perform the projections on the stacked system. Notably, where the number of instruments is large, relative to the number of observations, stacking the equations and instruments prior to performing the projection may be the only feasible way to compute 2SLS estimates.
To designate instruments for a stacked projection, you should use the @stackinst statement (note: this statement is only available for systems estimated by 2SLS or 3SLS; it is not available for systems estimated using GMM).
In a @stackinst statement, the “@STACKINST” keyword should be followed by a list of stacked instrument specifications. Each specification is a comma delimited list of series enclosed in parentheses (one per equation), describing the instruments to be constrained in a stacked specification.
For example, the following @stackinst specification creates two instruments in a three equation model:
@stackinst (z1,z2,z3) (m1,m1,m1)
This statement instructs EViews to form two stacked instruments, one by stacking the separate series Z1, Z2, and Z3, and the other formed by stacking M1 three times. The first-stage instrumental variables projection is then of the variables in the stacked system on the stacked instruments.
When working with systems that have a large number of equations, the above syntax may be unwieldy. For these cases, EViews provides a couple of shortcuts. First, for instruments that are identical in all equations, you may use an “*” after the comma to instruct EViews to repeat the specified series. Thus, the above statement is equivalent to:
@stackinst (z1,z2,z3) (m1,*)
Second, for non-identical instruments, you may specify a set of stacked instruments using an EViews group object, so long as the number of variables in the group is equal to the number of equations in the system. Thus, if you create a group Z with,
group z z1 z2 z3
the above statement can be simplified to:
@stackinst z (m1,*)
You can, of course, combine ordinary instrument and stacked instrument specifications. This situation is equivalent to having common and equation specific coefficients for vari-
How to Create and Specify a System—427
ables in your system. Simply think of the stacked instruments as representing common (coefficient) instruments, and ordinary instruments as representing equation specific (coefficient) instruments. For example, consider the system given by,
@stackinst (z1,z2,z3) (m1,*) @inst ia
y1 = c(1)*x1
y2 = c(1)*x2
y3 = c(1)*x3 @ ic
The stacked instruments for this specification may be represented as:
Z1 M1 IA C 0
0
0
0
0
Z2 M1
0
0
IA C
0
0
0
(31.2)
Z3 M1
0
0
0
0
IA C IC
so it is easy to see that this specification is equivalent to the following stacked specification,
Note that the constant instruments are added implicitly.
Additional Comments
•If you include a “C” in the stacked instrument list, it will not be included in the individual equations. If you do not include the “C” as a stacked instrument, it will be included as an instrument in every equation, whether specified explicitly or not.
•You should list all exogenous right-hand side variables as instruments for a given equation.
•Identification requires that there should be at least as many instruments (including the constant) in each equation as there are right-hand side variables in that equation.
•The @stackinst statement is only available for estimation by 2SLS and 3SLS. It is not currently supported for GMM.
•If you estimate your system using a method that does not use instruments, all instrument specification lines will be ignored.
428—Chapter 31. System Estimation
Starting Values
For systems that contain nonlinear equations, you can include a line that begins with param to provide starting values for some or all of the parameters. List pairs of parameters and values. For example:
param c(1) .15 b(3) .5
sets the initial values of C(1) and B(3). If you do not provide starting values, EViews uses the values in the current coefficient vector. In ARCH estimation, by default, EViews does provide a set of starting coefficients. Users are able to provide their own set of starting values by selecting User Supplied in the Starting coefficient value field located in the Options tab.
How to Estimate a System
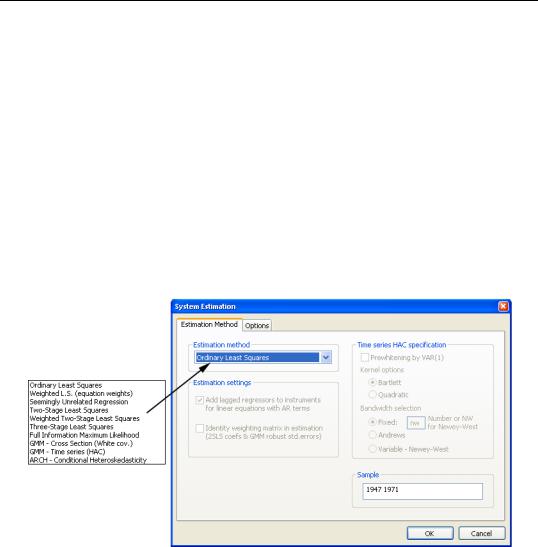
Once you have created and specified your system, you may push the Estimate button on the toolbar to bring up the System Estimation dialog.
The drop-down menu marked Estimation Method provides you with several options for the estimation method. You may choose from one of a number of methods for estimating the parameters of your specification.
The estimation dialog may change to reflect your choice, providing you with additional options. If you select an estimator which uses instrumental variables, a checkbox will appear, prompting you to choose whether to Add lagged regressors to instruments for linear equations with AR terms. As the checkbox label suggests, if selected, EViews will add lagged values of the dependent and independent variable to the instrument list when estimating AR models. The lag order for these instruments will match the AR order of the spec-
How to Create and Specify a System—429
ification. This automatic lag inclusion reflects the fact that EViews transforms the linear specification to a nonlinear specification when estimating AR models, and that the lagged values are ideal instruments for the transformed specification. If you wish to maintain precise control over the instruments added to your model, you should unselect this option.
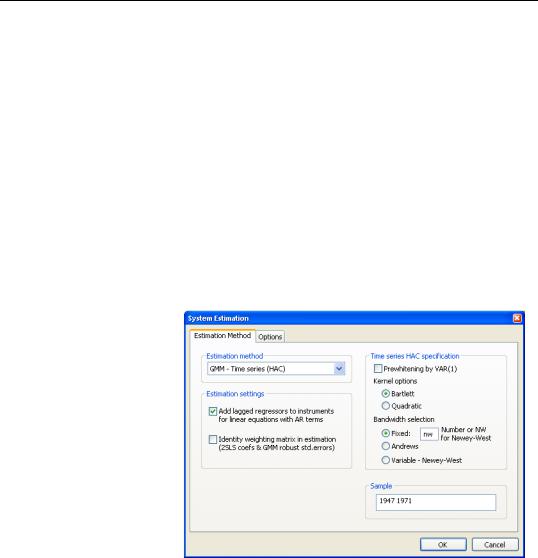
Additional options appear if you are estimating a GMM specification. Note that the GMMCross section option uses a weighting matrix that is robust to heteroskedasticity and contemporaneous correlation of unknown form, while the GMM-Time series (HAC) option extends this robustness to autocorrelation of unknown form.
If you select either GMM method, EViews will display a checkbox labeled Identity weighting matrix in estimation. If selected, EViews will estimate the model using identity weights, and will use the estimated coefficients and GMM specification you provide to compute a coefficient covariance matrix that is robust to cross-section heteroskedasticity (White) or heteroskedasticity and autocorrelation (Newey-West). If this option is not selected, EViews will use the GMM weights both in estimation, and in computing the coefficient covariances.
When you select the
GMM-Time series (HAC) option, the dialog displays additional options for specifying the weighting matrix. The new options will appear on the right side of the dialog. These options control the computation of the heteroskedasticity and autocorrelation robust (HAC) weighting matrix. See “Technical Discussion” on
page 446 for a more detailed discussion of these options.
The Kernel Options determines the functional form of the kernel used to weight the autocovariances to compute the weighting matrix. The Bandwidth Selection option determines how the weights given by the kernel change with the lags of the autocovariances in the computation of the weighting matrix. If you select Fixed bandwidth, you may enter a number for the bandwidth or type nw to use Newey and West’s fixed bandwidth selection criterion.
430—Chapter 31. System Estimation
The Prewhitening option runs a preliminary VAR(1) prior to estimation to “soak up” the correlation in the moment conditions.
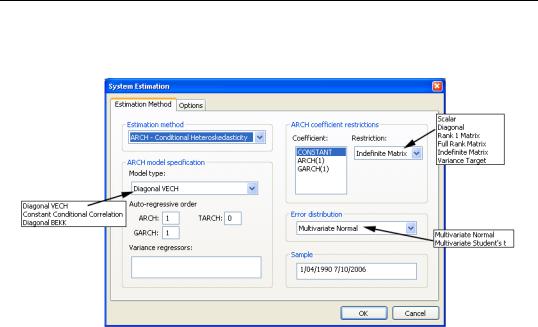
If the ARCH - Conditional Heteroskedasticity method is selected, the dialog displays the options appropriate for ARCH models. Model type allows you to select among three different multivariate ARCH models: Diagonal VECH, Constant Conditional Correlation (CCC), and Diagonal BEKK. Auto-regressive order indicates the number of autoregressive terms included in the model. You may use the Variance Regressors edit field to specify any regressors in the variance equation.
The coefficient specifications for the auto-regressive terms and regressors in the variance equation may be fine-tuned using the controls in the ARCH coefficient restrictions section of the dialog page. Each auto-regression or regressor term is displayed in the Coefficient list. You should select a term to modify it, and in the Restriction field select a type coefficient specification for that term. For the Diagonal VECH model, each of the coefficient matrices may be restricted to be Scalar, Diagonal, Rank One, Full Rank, Indefinite Matrix or (in the case of the constant coefficient) Variance Target. The options for the BEKK model behave the same except that the ARCH, GARCH, and TARCH term is restricted to be Diagonal. For the CCC model, Scalar is the only option for ARCH, TARCH and GARCH terms, Scalar and Variance Target are allowed or the constant term. For for exogenous variables you may choose between Individual and Common, indicating whether the parameters are restricted to be the same for all variance equations (common) or are unrestricted.
By default, the conditional distribution of the error terms is assumed to be Multivariate Normal. You have the option of instead using Multivariate Student's t by selecting it in the
Error distribution dropdown list.
How to Create and Specify a System—431
Options
For weighted least squares, SUR, weighted TSLS, 3SLS, GMM, and nonlinear systems of equations, there are additional issues involving the procedure for computing the GLS weighting matrix and the coefficient vector and for ARCH system, the coefficient vector used in estimation, as well as backcasting and robust standard error options.
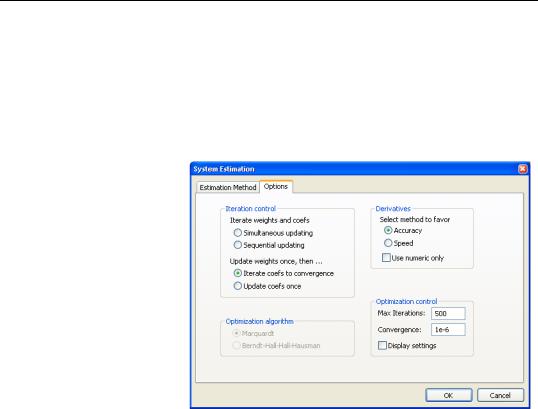
To specify the method used in iteration, click on the Options tab.
The estimation option controls the method of iterating over coefficients, over the weighting matrices, or both:
•Update weights once, then—Iter- ate coefs to convergence is the default method.
By default, EViews carries out a first-stage estimation of the coefficients using
no weighting matrix (the identity matrix). Using starting values obtained from OLS (or TSLS, if there are instruments), EViews iterates the first-stage estimates until the coefficients converge. If the specification is linear, this procedure involves a single OLS or TSLS regression.
The residuals from this first-stage iteration are used to form a consistent estimate of the weighting matrix.
In the second stage of the procedure, EViews uses the estimated weighting matrix in forming new estimates of the coefficients. If the model is nonlinear, EViews iterates the coefficient estimates until convergence.
•Update weights once, then—Update coefs once performs the first-stage estimation of the coefficients, and constructs an estimate of the weighting matrix. In the second stage, EViews does not iterate the coefficients to convergence, instead performing a single coefficient iteration step. Since the first stage coefficients are consistent, this one-step update is asymptotically efficient, but unless the specification is linear, does not produce results that are identical to the first method.
•Iterate Weights and Coefs—Simultaneous updating updates both the coefficients and the weighting matrix at each iteration. These steps are then repeated until both
432—Chapter 31. System Estimation
the coefficients and weighting matrix converge. This is the iteration method employed in EViews prior to version 4.
•Iterate Weights and Coefs—Sequential updating repeats the default method of updating weights and then iterating coefficients to convergence until both the coefficients and the weighting matrix converge.
Note that all four of the estimation techniques yield results that are asymptotically efficient. For linear models, the two Iterate Weights and Coefs options are equivalent, and the two One-Step Weighting Matrix options are equivalent, since obtaining coefficient estimates does not require iteration.
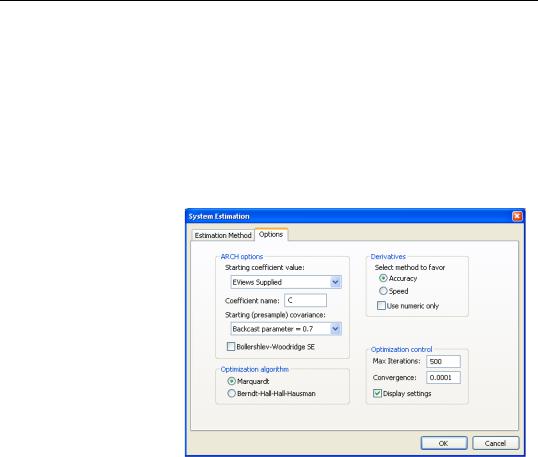
When ARCH is the estimation method a set of ARCH options appears:
•Starting coefficient value indicates what starting values EViews should use to start the iteration process. By default
EViews Supplied is set. You can also select User Supplied which allows you to set
your own starting coefficient via the C coefficient vector or another of your choice.
•Coefficient name specifies the name of the coefficient to be used in the variance equation. This can be different from the mean equation.
•Starting (presample) covariance indicates the method by which presample conditional variance and expected innovation should be calculated. Initial variance for the conditional variance are set using backcasting of the innovations,
