
- •Preface
- •Part IV. Basic Single Equation Analysis
- •Chapter 18. Basic Regression Analysis
- •Equation Objects
- •Specifying an Equation in EViews
- •Estimating an Equation in EViews
- •Equation Output
- •Working with Equations
- •Estimation Problems
- •References
- •Chapter 19. Additional Regression Tools
- •Special Equation Expressions
- •Robust Standard Errors
- •Weighted Least Squares
- •Nonlinear Least Squares
- •Stepwise Least Squares Regression
- •References
- •Chapter 20. Instrumental Variables and GMM
- •Background
- •Two-stage Least Squares
- •Nonlinear Two-stage Least Squares
- •Limited Information Maximum Likelihood and K-Class Estimation
- •Generalized Method of Moments
- •IV Diagnostics and Tests
- •References
- •Chapter 21. Time Series Regression
- •Serial Correlation Theory
- •Testing for Serial Correlation
- •Estimating AR Models
- •ARIMA Theory
- •Estimating ARIMA Models
- •ARMA Equation Diagnostics
- •References
- •Chapter 22. Forecasting from an Equation
- •Forecasting from Equations in EViews
- •An Illustration
- •Forecast Basics
- •Forecasts with Lagged Dependent Variables
- •Forecasting with ARMA Errors
- •Forecasting from Equations with Expressions
- •Forecasting with Nonlinear and PDL Specifications
- •References
- •Chapter 23. Specification and Diagnostic Tests
- •Background
- •Coefficient Diagnostics
- •Residual Diagnostics
- •Stability Diagnostics
- •Applications
- •References
- •Part V. Advanced Single Equation Analysis
- •Chapter 24. ARCH and GARCH Estimation
- •Basic ARCH Specifications
- •Estimating ARCH Models in EViews
- •Working with ARCH Models
- •Additional ARCH Models
- •Examples
- •References
- •Chapter 25. Cointegrating Regression
- •Background
- •Estimating a Cointegrating Regression
- •Testing for Cointegration
- •Working with an Equation
- •References
- •Binary Dependent Variable Models
- •Ordered Dependent Variable Models
- •Censored Regression Models
- •Truncated Regression Models
- •Count Models
- •Technical Notes
- •References
- •Chapter 27. Generalized Linear Models
- •Overview
- •How to Estimate a GLM in EViews
- •Examples
- •Working with a GLM Equation
- •Technical Details
- •References
- •Chapter 28. Quantile Regression
- •Estimating Quantile Regression in EViews
- •Views and Procedures
- •Background
- •References
- •Chapter 29. The Log Likelihood (LogL) Object
- •Overview
- •Specification
- •Estimation
- •LogL Views
- •LogL Procs
- •Troubleshooting
- •Limitations
- •Examples
- •References
- •Part VI. Advanced Univariate Analysis
- •Chapter 30. Univariate Time Series Analysis
- •Unit Root Testing
- •Panel Unit Root Test
- •Variance Ratio Test
- •BDS Independence Test
- •References
- •Part VII. Multiple Equation Analysis
- •Chapter 31. System Estimation
- •Background
- •System Estimation Methods
- •How to Create and Specify a System
- •Working With Systems
- •Technical Discussion
- •References
- •Vector Autoregressions (VARs)
- •Estimating a VAR in EViews
- •VAR Estimation Output
- •Views and Procs of a VAR
- •Structural (Identified) VARs
- •Vector Error Correction (VEC) Models
- •A Note on Version Compatibility
- •References
- •Chapter 33. State Space Models and the Kalman Filter
- •Background
- •Specifying a State Space Model in EViews
- •Working with the State Space
- •Converting from Version 3 Sspace
- •Technical Discussion
- •References
- •Chapter 34. Models
- •Overview
- •An Example Model
- •Building a Model
- •Working with the Model Structure
- •Specifying Scenarios
- •Using Add Factors
- •Solving the Model
- •Working with the Model Data
- •References
- •Part VIII. Panel and Pooled Data
- •Chapter 35. Pooled Time Series, Cross-Section Data
- •The Pool Workfile
- •The Pool Object
- •Pooled Data
- •Setting up a Pool Workfile
- •Working with Pooled Data
- •Pooled Estimation
- •References
- •Chapter 36. Working with Panel Data
- •Structuring a Panel Workfile
- •Panel Workfile Display
- •Panel Workfile Information
- •Working with Panel Data
- •Basic Panel Analysis
- •References
- •Chapter 37. Panel Estimation
- •Estimating a Panel Equation
- •Panel Estimation Examples
- •Panel Equation Testing
- •Estimation Background
- •References
- •Part IX. Advanced Multivariate Analysis
- •Chapter 38. Cointegration Testing
- •Johansen Cointegration Test
- •Single-Equation Cointegration Tests
- •Panel Cointegration Testing
- •References
- •Chapter 39. Factor Analysis
- •Creating a Factor Object
- •Rotating Factors
- •Estimating Scores
- •Factor Views
- •Factor Procedures
- •Factor Data Members
- •An Example
- •Background
- •References
- •Appendix B. Estimation and Solution Options
- •Setting Estimation Options
- •Optimization Algorithms
- •Nonlinear Equation Solution Methods
- •References
- •Appendix C. Gradients and Derivatives
- •Gradients
- •Derivatives
- •References
- •Appendix D. Information Criteria
- •Definitions
- •Using Information Criteria as a Guide to Model Selection
- •References
- •Appendix E. Long-run Covariance Estimation
- •Technical Discussion
- •Kernel Function Properties
- •References
- •Index
- •Symbols
- •Numerics

Chapter 28. Quantile Regression
While the great majority of regression models are concerned with analyzing the conditional mean of a dependent variable, there is increasing interest in methods of modeling other aspects of the conditional distribution. One increasingly popular approach, quantile regression, models the quantiles of the dependent variable given a set of conditioning variables.
As originally proposed by Koenker and Bassett (1978), quantile regression provides estimates of the linear relationship between regressors X and a specified quantile of the dependent variable Y . One important special case of quantile regression is the least absolute deviations (LAD) estimator, which corresponds to fitting the conditional median of the response variable.
Quantile regression permits a more complete description of the conditional distribution than conditional mean analysis alone, allowing us, for example, to describe how the median, or perhaps the 10th or 95th percentile of the response variable, are affected by regressor variables. Moreover, since the quantile regression approach does not require strong distributional assumptions, it offers a distributionally robust method of modeling these relationships.
The remainder of this chapter describes the basics of performing quantile regression in EViews. We begin with a walkthrough showing how to estimate a quantile regression specification and describe the output from the procedure. Next we examine the various views and procedures that one may perform using an estimated quantile regression equation. Lastly, we provide background information on the quantile regression model.
Estimating Quantile Regression in EViews
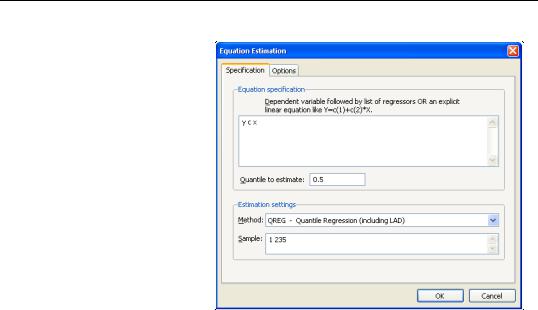
To estimate a quantile regression specification in EViews you may select Object/New Object.../Equation or Quick/Estimate Equation… from the main menu, or simply type the keyword equation in the command window. From the main estimation dialog you should select QREG - Quantile Regression (including LAD). Alternately, you may type qreg in the command window.
332—Chapter 28. Quantile Regression
EViews will open the quantile regression form of the
Equation Estimation dialog.
Specification
The dialog has two pages. The first page, depicted here, is used to specify the variables in the conditional quantile function, the quantile to estimate, and the sample of observations to use.
You may enter the Equation specification using a list of the dependent and regressor variables, as depicted here, or you may enter an explicit
expression. Note that if you enter an explicit expression it must be linear in the coefficients.
The Quantile to estimate edit field is where you will enter your desired quantile. By default, EViews estimates the median regression as depicted here, but you may enter any value between 0 and 1 (though values very close to 0 and 1 may cause estimation difficulties).
Here we specify a conditional median function for Y that depends on a constant term and the series X. EViews will estimate the LAD estimator for the entire sample of 235 observations.
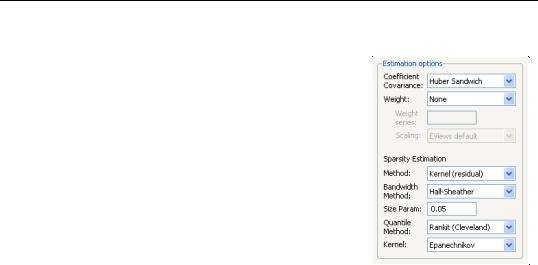
Estimation Options
Most of the quantile regression settings are set using this page. The options on the left-hand side of the page control the method for computing the coefficient covariances, allow you to specify a weight series for weighted estimation, and specify the method for computing scalar sparsity estimates.
Estimating Quantile Regression in EViews—333
Quantile Regression Options
The combo box labeled Coefficient Covariance is where you will choose your method of computing covariances: computing Ordinary (IID) covariances, using a Huber Sandwich method, or using Bootstrap resampling. By default, EViews uses the Huber Sandwich calculations which are valid under independent but non-identical sampling.
Just below the combo box is an section Weight, where you may define observations weights. The data will be transformed prior to estimation using this specification.
(See “Weighted Least Squares” on page 36 for a discussion of the settings).
The remaining settings in this section control the estima-
tion of the scalar sparsity value. Different options are available for different Coefficient Covariance settings. For ordinary or bootstrap covariances you may choose either Siddiqui (mean fitted), Kernel (residual), or Siddiqui (residual) as your sparsity estimation method, while if the covariance method is set to Huber Sandwich, only the Siddiqui (mean fitted) and Kernel (residual) methods are available.
There are additional options for the bandwidth method (and associated size parameter if relevant), the method for computing empirical quantiles (used to estimate the sparsity or the kernel bandwidth), and the choice of kernel function. Most of these settings should be selfexplanatory; if necessary, see the discussion in “Sparsity Estimation,” beginning on
page 344 for details.
It is worth mentioning that the sparsity estimation options are always relevant, since EViews always computes and reports a scalar sparsity estimate, even if it is not used in computing the covariance matrix. In particular, a sparsity value is estimated even when you compute the asymptotic covariance using a Huber Sandwich method. The sparsity estimate will be used in non-robust quasi-likelihood ratio tests statistics as necessary.
Iteration Control
The iteration control section offers the standard edit field for changing the maximum number of iterations, a combo box for specifying starting values, and a check box for displaying the estimation settings in the output. Note that the default starting value for quantile regression is 0, but you may choose a fraction of the OLS estimates, or provide a set of user specified values.

334—Chapter 28. Quantile Regression
Bootstrap Settings
When you select Bootstrap in the Coefficient Covariance combo, the right side of the dialog changes to offer a set of bootstrap options.
You may use the Method combo box to choose from one of four bootstrap methods: Residual, XY-pair, MCMB, MCMB- A. See “Bootstrapping,” beginning on page 348 for a discussion of the various methods. The default method is XY-pair.
Just below the combo box are two edit fields labeled Replications and No. of obs. By default, EViews will perform 100 bootstrap replications, but you may override this by entering your desired value. The No. of obs. edit field controls the size of the bootstrap sample. If the edit field is left blank,
EViews will draw samples of the same size as the original data. There is some evidence that specifying a bootstrap sample size m smaller than n may produce more accurate results, especially for very large sample sizes; Koenker (2005, p. 108) provides a brief summary.
To save the results of your bootstrap replications in a matrix object, enter the name in the Output edit field.
The last two items control the generation of random numbers. The Random generator combo should be self-explanatory. Simply use the combo to choose your desired generator. EViews will initialize the combo using the default settings for the choice of generator.
The random Seed field requires some discussion. By default, the first time that you perform a bootstrap for a given equation, the Seed edit field will be blank; you may provide your own integer value, if desired. If an initial seed is not provided, EViews will randomly select a seed value. The value of this initial seed will be saved with the equation so that by default, subsequent estimation will employ the same seed, allowing you to replicate results when reestimating the equation, and when performing tests. If you wish to use a different seed, simply enter a value in the Seed edit field or press the Clear button to have EViews draw a new random seed value.
Estimation Output
Once you have provided your quantile regression specification and specified your options, you may click on OK to estimate your equation. Unless you are performing bootstrapping with a very large number of observations, the estimation results should be displayed shortly.
Our example uses the Engel dataset containing food expenditure and household income considered by Koenker (2005, p. 78-79, 297-307). The default model estimates the median of food expenditure Y as a function of a constant term and household income X.

Estimating Quantile Regression in EViews—335
Dependent Variable: Y
Method: Quantile Regression (Median)
Date: 08/12/09 Time: 11:46
Sample: 1 235
Included observations: 235
Huber Sandwich Standard Errors & Covariance
Sparsity method: Kernel (Epanechnikov) using residuals
Bandwidth method: Hall-Sheather, bw=0.15744
Estimation successfully identifies unique optimal solution
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
C |
81.48225 |
24.03494 |
3.390158 |
0.0008 |
X |
0.560181 |
0.031370 |
17.85707 |
0.0000 |
|
|
|
|
|
|
|
|
|
|
Pseudo R-squared |
0.620556 |
Mean dependent var |
624.1501 |
|
Adjusted R-squared |
0.618927 |
S.D. dependent var |
276.4570 |
|
S.E. of regression |
120.8447 |
Objective |
|
8779.966 |
Quantile dependent var |
582.5413 |
Restr. objective |
|
23139.03 |
Sparsity |
209.3504 |
Quasi-LR statistic |
548.7091 |
|
Prob(Quasi-LR stat) |
0.000000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
The top portion of the output displays the estimation settings. Here we see that our estimates use the Huber sandwich method for computing the covariance matrix, with individual sparsity estimates obtained using kernel methods. The bandwidth uses the Hall and Sheather formula, yielding a value of 0.15744.
Below the header information are the coefficients, along with standard errors, t-statistics and associated p-values. We see that both coefficients are statistically significantly different from zero and conventional levels.
The bottom portion of the output reports the Koenker and Machado (1999) goodness-of-fit measure (pseudo R-squared), and adjusted version of the statistic, as well as the scalar estimate of the sparsity using the kernel method. Note that this scalar estimate is not used in the computation of the standard errors in this case since we are employing the Huber sandwich method.
Also reported are the minimized value of the objective function (“Objective”), the minimized constant-only version of the objective (“Objective (const. only)”), the constant-only coefficient estimate (“Quantile dependent var”), and the corresponding Ln(t) form of the Quasi-LR statistic and associated probability for the difference between the two specifications (Koenker and Machado, 1999). Note that despite the fact that the coefficient covariances are computed using the robust Huber Sandwich, the QLR statistic assumes i.i.d. errors and uses the estimated value of the sparsity.
The reported S.E. of the regression is based on the usual d.f. adjusted sample variance of the residuals. This measure of scale is used in forming standardized residuals and forecast standard errors. It is replaced by the Koenker and Machado (1999) scale estimator in the compu-
