Examples

308—Chapter 27. Generalized Linear Models

Dependent Variable: NUMB

Method: Generalized Linear Model (Quadratic Hill Climbing)

Date: 06/15/09 Time: 09:31

Sample: 1 103

Included observations: 103

Family: Normal

Link: Log

Dispersion computed using Pearson Chi-Square

Coefficient covariance computed using observed Hessian

Convergence achieved after 5 iterations

The top portion of the output displays the estimation settings and basic results, in particular the choice of algorithm (Quadratic Hill Climbing), distribution family (Normal), and link function (Log), as well as the dispersion estimator, coefficient covariance estimator, and estimation status. We see that the dispersion estimator is based on the Pearson x2 statistic and the coefficient covariance is computed using the inverse of the observed Hessian.

The coefficient estimates indicate that IP is positively related to the number of strikes, and that the relationship is statistically significant at conventional levels. The FEB dummy variable is negatively related to NUMB, but the relationship is not statistically significant.

The bottom portion of the output displays various descriptive statistics. Note that in place of some of the more familiar statistics, EViews reports the deviance, deviance statistic (deviance divided by the degrees-of-freedom) restricted deviance (deviance for the model with only a constant), and the corresponding LR test statistic and probability. The test indicates that the IP and FEB variables are jointly significant at roughly the 3% level. Also displayed are the sum-of-squared Pearson residuals and the estimate of the dispersion, which in this example is the Pearson statistic.

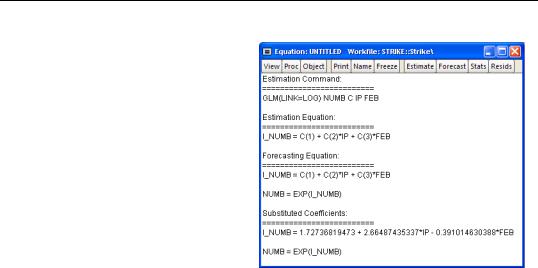
Examples—309

It may be instructive to examine the representations view of this equation. Simply go to the equation toolbar or the main menu and click on

View/Representations to display the view.

Notably, the representations view displays both the specification of the linear predictor (I_NUMB) as well as the mean specification (EXP(I_NUMB)) in terms of the EViews coefficient names, and in terms of the estimated values. These are the expressions used when fore-

casting the index or the dependent variable using the Forecast procedure (see “Forecasting” on page 316).

Binomial

We illustrate the estimation of GLM binomial logistic regression using a simple example from Agresti (2007, Table 3.1, p. 69) examining the relationship between snoring and heart disease. The data in the first page of the workfile “Snoring.WF1” consist of grouped binomial response data for 2,484 subjects divided into four risk factor groups for snoring level (SNORE), coded as 0, 2, 4, 5. Associated with each of the four groups is the number of individuals in the group exhibiting heart disease (DISEASE) as well as a total group size (TOTAL).

We may estimate a logistic regression model for these data in either raw frequency or proportions form.

To estimate the model in raw frequency form, bring up the GLM equation dialog, enter the linear predictor specification:

disease c snore

310—Chapter 27. Generalized Linear Models

select Binomial Count in the Family combo, and enter “TOTAL” in the Number of trials edit field. Next switch over to the Options page and turn off the d.f. Adjustment for the coefficient covariance. Click on OK to estimate the equation.

Dependent Variable: DISEASE

Method: Generalized Linear Model (Quadratic Hill Climbing) Date: 06/15/09 Time: 16:20

Sample: 1 4

Included observations: 4

Family: Binomial Count (n = TOTAL) Link: Logit

Dispersion fixed at 1

Coefficient covariance computed using observed Hessian Summary statistics are for the binomial proportions and implicit

variance weights used in estimation Convergence achieved after 4 iterations

No d.f. adjustment for standard errors & covariance

The output header shows relevant information for the estimation procedure. Note in particular the EViews message that summary statistics are computed for the binomial proportions data. This message is a hint at the fact that EViews estimates the binomial count model by scaling the dependent variable by the number of trials, and estimating the corresponding proportions specification.

Equivalently, you could have specified the model in proportions form. Simply enter the linear predictor specification:

disease/total c snore

with Binomial Proportions specified in the Family combo and “TOTAL” entered in the

Number of trials edit field.

312—Chapter 27. Generalized Linear Models

In this representation, DISEASE is an indicator for whether the record corresponds to individuals with heart disease or not, and N is the number of individuals in the category.

Estimation of the equivalent GLM model specified using the frequency weighted data is straightforward. Simply enter the linear predictor specification:

disease c snore

with either Binomial Proportions or Binomial Count specified in the Family combo. Since each observation corresponds to a binary indicator, you should enter “1” enter as the Number of trials edit field. The multiple individuals in the category are handled by entering “N” in the Frequency weights field in the Options page.

Dependent Variable: DISEASE

Method: Generalized Linear Model (Quadratic Hill Climbing)

Date: 06/16/09 Time: 14:45

Sample: 1 8

Included cases: 8

Total observations: 2484

Family: Binomial Count (n = 1)

Link: Logit

Frequency weight series: N

Dispersion fixed at 1

Coefficient covariance computed using observed Hessian

Convergence achieved after 6 iterations

No d.f. adjustment for standard errors & covariance

Note that while a number of the summary statistics differ due to the different representation of the data (notably the Deviance and Pearson SSRs), the coefficient estimates and LR test statistics in this case are identical to those outlined above. There will, however, be substantive differences between the two results in settings when the dispersion is estimated since the effective number of observations differs in the two settings.

314—Chapter 27. Generalized Linear Models

Dependent Variable: PRATE

Method: Generalized Linear Model (Quadratic Hill Climbing)

Date: 08/12/09 Time: 11:28

Sample: 1 4735 IF MRATE <=1

Included observations: 3784

Family: Binomial Proportion (trials = 1) (quasi-likelihood)

Link: Logit

Dispersion computed using Pearson Chi-Square

Coefficient covariance computed using observed Hessian

Convergence achieved after 8 iterations

Papke and Wooldridge offer a detailed analysis of the results (p. 628-629), which we will not duplicate here. We will point out that the estimate of the dispersion (0.191798) taken from the Pearson statistic is far from the restricted value of 1.0.

The results using the QML with GLM standard errors rely on validity of the GLM assumption for the variance given in Equation (27.2), an assumption that may be too restrictive. We may instead estimate the equation without imposing a particular conditional variance specification by computing our estimates using a robust Huber-White sandwich method. Click on Estimate to bring up the equation dialog, select the Options tab, then change the Covariance method from Default to Huber/White. Click on OK to estimate the revised specification: