
- •Preface
- •Part IV. Basic Single Equation Analysis
- •Chapter 18. Basic Regression Analysis
- •Equation Objects
- •Specifying an Equation in EViews
- •Estimating an Equation in EViews
- •Equation Output
- •Working with Equations
- •Estimation Problems
- •References
- •Chapter 19. Additional Regression Tools
- •Special Equation Expressions
- •Robust Standard Errors
- •Weighted Least Squares
- •Nonlinear Least Squares
- •Stepwise Least Squares Regression
- •References
- •Chapter 20. Instrumental Variables and GMM
- •Background
- •Two-stage Least Squares
- •Nonlinear Two-stage Least Squares
- •Limited Information Maximum Likelihood and K-Class Estimation
- •Generalized Method of Moments
- •IV Diagnostics and Tests
- •References
- •Chapter 21. Time Series Regression
- •Serial Correlation Theory
- •Testing for Serial Correlation
- •Estimating AR Models
- •ARIMA Theory
- •Estimating ARIMA Models
- •ARMA Equation Diagnostics
- •References
- •Chapter 22. Forecasting from an Equation
- •Forecasting from Equations in EViews
- •An Illustration
- •Forecast Basics
- •Forecasts with Lagged Dependent Variables
- •Forecasting with ARMA Errors
- •Forecasting from Equations with Expressions
- •Forecasting with Nonlinear and PDL Specifications
- •References
- •Chapter 23. Specification and Diagnostic Tests
- •Background
- •Coefficient Diagnostics
- •Residual Diagnostics
- •Stability Diagnostics
- •Applications
- •References
- •Part V. Advanced Single Equation Analysis
- •Chapter 24. ARCH and GARCH Estimation
- •Basic ARCH Specifications
- •Estimating ARCH Models in EViews
- •Working with ARCH Models
- •Additional ARCH Models
- •Examples
- •References
- •Chapter 25. Cointegrating Regression
- •Background
- •Estimating a Cointegrating Regression
- •Testing for Cointegration
- •Working with an Equation
- •References
- •Binary Dependent Variable Models
- •Ordered Dependent Variable Models
- •Censored Regression Models
- •Truncated Regression Models
- •Count Models
- •Technical Notes
- •References
- •Chapter 27. Generalized Linear Models
- •Overview
- •How to Estimate a GLM in EViews
- •Examples
- •Working with a GLM Equation
- •Technical Details
- •References
- •Chapter 28. Quantile Regression
- •Estimating Quantile Regression in EViews
- •Views and Procedures
- •Background
- •References
- •Chapter 29. The Log Likelihood (LogL) Object
- •Overview
- •Specification
- •Estimation
- •LogL Views
- •LogL Procs
- •Troubleshooting
- •Limitations
- •Examples
- •References
- •Part VI. Advanced Univariate Analysis
- •Chapter 30. Univariate Time Series Analysis
- •Unit Root Testing
- •Panel Unit Root Test
- •Variance Ratio Test
- •BDS Independence Test
- •References
- •Part VII. Multiple Equation Analysis
- •Chapter 31. System Estimation
- •Background
- •System Estimation Methods
- •How to Create and Specify a System
- •Working With Systems
- •Technical Discussion
- •References
- •Vector Autoregressions (VARs)
- •Estimating a VAR in EViews
- •VAR Estimation Output
- •Views and Procs of a VAR
- •Structural (Identified) VARs
- •Vector Error Correction (VEC) Models
- •A Note on Version Compatibility
- •References
- •Chapter 33. State Space Models and the Kalman Filter
- •Background
- •Specifying a State Space Model in EViews
- •Working with the State Space
- •Converting from Version 3 Sspace
- •Technical Discussion
- •References
- •Chapter 34. Models
- •Overview
- •An Example Model
- •Building a Model
- •Working with the Model Structure
- •Specifying Scenarios
- •Using Add Factors
- •Solving the Model
- •Working with the Model Data
- •References
- •Part VIII. Panel and Pooled Data
- •Chapter 35. Pooled Time Series, Cross-Section Data
- •The Pool Workfile
- •The Pool Object
- •Pooled Data
- •Setting up a Pool Workfile
- •Working with Pooled Data
- •Pooled Estimation
- •References
- •Chapter 36. Working with Panel Data
- •Structuring a Panel Workfile
- •Panel Workfile Display
- •Panel Workfile Information
- •Working with Panel Data
- •Basic Panel Analysis
- •References
- •Chapter 37. Panel Estimation
- •Estimating a Panel Equation
- •Panel Estimation Examples
- •Panel Equation Testing
- •Estimation Background
- •References
- •Part IX. Advanced Multivariate Analysis
- •Chapter 38. Cointegration Testing
- •Johansen Cointegration Test
- •Single-Equation Cointegration Tests
- •Panel Cointegration Testing
- •References
- •Chapter 39. Factor Analysis
- •Creating a Factor Object
- •Rotating Factors
- •Estimating Scores
- •Factor Views
- •Factor Procedures
- •Factor Data Members
- •An Example
- •Background
- •References
- •Appendix B. Estimation and Solution Options
- •Setting Estimation Options
- •Optimization Algorithms
- •Nonlinear Equation Solution Methods
- •References
- •Appendix C. Gradients and Derivatives
- •Gradients
- •Derivatives
- •References
- •Appendix D. Information Criteria
- •Definitions
- •Using Information Criteria as a Guide to Model Selection
- •References
- •Appendix E. Long-run Covariance Estimation
- •Technical Discussion
- •Kernel Function Properties
- •References
- •Index
- •Symbols
- •Numerics

698—Chapter 38. Cointegration Testing
Date: 05/11/09 Time: 16:01
Series: P_T S_T PSTAR_T
Sample: 1973M01 1989M10 Included observations: 202
Null hypothesis: Series are not cointegrated Cointegrating equation deterministics: C Additional regressor deterministics: @TREND
Long-run variance estimate (Bartlett kernel, User bandwidth = 13.0000)
No d.f. adjustment for variances
Dependent |
tau-statistic |
Prob.* |
z-statistic |
Prob.* |
P_T |
-2.023222 |
0.7645 |
-7.542281 |
0.8039 |
S_T |
-1.723248 |
0.8710 |
-6.457868 |
0.8638 |
PSTAR_T |
-1.997466 |
0.7753 |
-7.474681 |
0.8078 |
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) p-values. |
|
|
|
|
Intermediate Results: |
|
|
|
|
|
|
P_T |
S_T |
PSTAR_T |
Rho - 1 |
|
-0.016689 |
-0.014395 |
-0.017550 |
Bias corrected Rho - 1 (Rho* - 1) |
-0.037524 |
-0.032129 |
-0.037187 |
|
Rho* S.E. |
|
0.018547 |
0.018644 |
0.018617 |
Residual variance |
|
0.162192 |
6.411674 |
0.619376 |
Long-run residual variance |
0.408224 |
13.02214 |
1.419722 |
|
Long-run residual autocovariance |
0.123016 |
3.305234 |
0.400173 |
|
Bandwidth |
|
13.00000 |
13.00000 |
13.00000 |
Number of observations |
201 |
201 |
201 |
|
Number of stochastic trends** |
2 |
2 |
2 |
|
**Number of stochastic trends in asymptotic distribution
In contrast with the Engle-Granger tests, the results are quite similar for all six of the tests with the Phillips-Ouliaris test not rejecting the null hypothesis that the series are not cointegrated. As before, the bottom portion of the output displays intermediate results for the test associated with each dependent variable.
Panel Cointegration Testing
The extensive interest in and the availability of panel data has led to an emphasis on extending various statistical tests to panel data. Recent literature has focused on tests of cointegration in a panel setting. EViews will compute one of the following types of panel cointegration tests: Pedroni (1999), Pedroni (2004), Kao (1999) and a Fisher-type test using an underlying Johansen methodology (Maddala and Wu 1999).
Performing Panel Cointegration Tests in EViews
You may perform a cointegration test using either a Pool object or a Group in a panel workfile setting. We focus here on the panel setting; conducting a cointegration test using a Pool
Panel Cointegration Testing—699
involves only minor differences in specification (see “Performing Cointegration Tests,” beginning on page 582 for a discussion of testing in the pooled data setting).
To perform the panel cointegration test using a Group object you should first make certain you are in a panel structured workfile (Chapter 36. “Working with Panel Data,” on
page 615). If you have a panel workfile with a single cross-section in the sample, you may perform one of the standard single-equation cointegration tests using your subsample.
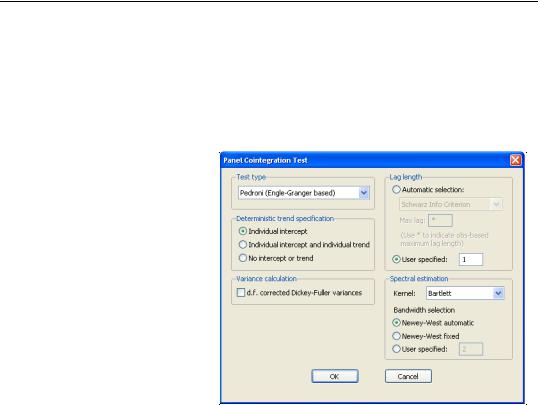
Next, open an EViews group containing the series of interest, and select Views/Cointegration Test/Panel Cointegration Test… to display the cointegration dialog.
The combo box at the top of the dialog box allow you to choose between three types of tests: Pedroni (Engle-
Granger based), Kao (EngleGranger based), Fisher (combined Johansen). As you select different test types, the remainder of the dialog will change to present you
with different options. Here, we see the options associated with the Pedroni test.
(Note, the Pedroni test will only be available for groups containing seven or fewer series.)
The customizable options associated with Pedroni and Kao tests are very similar to the options found in panel unit root testing (“Panel Unit Root Test” on page 391).
The Deterministic trend specification portion of the dialog specifies the exogenous regressors to be included in the second-stage regression. You should select Individual intercept if you wish to include individual fixed effects, Individual intercept and individual trend if you wish to include both individual fixed effects and trends, or No intercept or trend to include no regressors. The Kao test only allows for Individual intercept.
The Lag length section is used to determine the number of lags to be included in the second stage regression. If you select Automatic selection, EViews will determine the optimum lag using the information criterion specified in the combo box (Akaike, Schwarz, HannanQuinn). In addition you may provide a Maximum lag to be used in automatic selection. An empty field will instruct EViews to calculate the maximum lag for each cross-section based on the number of observations. The default maximum lag length for cross-section i is computed as:
700—Chapter 38. Cointegration Testing
int(min((Ti – k) § 3, 12) (Ti § 100)1 § 4)
where Ti is the length of the cross-section i . Alternatively, you may provide your own value by selecting User specified, and entering a value in the edit field.
The Pedroni test employs both parametric and non-parametric kernel estimation of the long run variance. You may use the Variance calculation and Lag length sections to control the computation of the parametric variance estimators. The Spectral estimation portion of the dialog allows you to specify settings for the non-parametric estimation. You may select from a number of kernel types (Bartlett, Parzen, Quadratic spectral) and specify how the bandwidth is to be selected (Newey-West automatic, Newey-West fixed, User specified). The Newey-West fixed bandwidth is given by 4(T i § 100)2 § 9 . The Kao test uses the Lag length and the Spectral estimation portion of the dialog settings as described below.
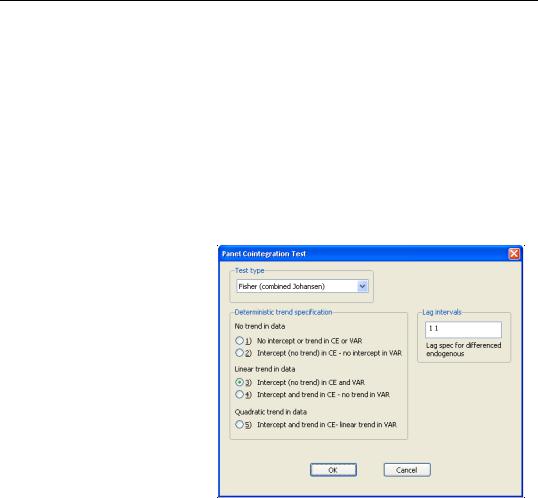
Here, we see the options for the Fisher test selection. These options are similar to the options available in the Johansen cointegration test (“Johansen Cointegration Test,” beginning on
page 685).
The Deterministic trend specification section determines the type of exogenous trend to be used.
The Lag intervals section specifies the lag-pair to be used in estimation.
Panel Cointegration Details
Here, we provide a brief description of the cointegration tests supported by EViews. The Pedroni and Kao tests are based on Engle-Granger (1987) two-step (residual-based) cointegration tests. The Fisher test is a combined Johansen test.
Pedroni (Engle-Granger based) Cointegration Tests
The Engle-Granger (1987) cointegration test is based on an examination of the residuals of a spurious regression performed using I(1) variables. If the variables are cointegrated then the residuals should be I(0). On the other hand if the variables are not cointegrated then the residuals will be I(1). Pedroni (1999, 2004) and Kao (1999) extend the Engle-Granger framework to tests involving panel data.

Panel Cointegration Testing—701
Pedroni proposes several tests for cointegration that allow for heterogeneous intercepts and trend coefficients across cross-sections. Consider the following regression
yit = ai + dit + b1ix1i, t + b2ix2i, t + º + bMixMi, t + ei, t |
(38.6) |
for t = 1, º, T ; i = 1, º, N ; m = 1, º, M ; where y and x are assumed to be integrated of order one, e.g. I(1). The parameters ai and di are individual and trend effects which may be set to zero if desired.
Under the null hypothesis of no cointegration, the residuals ei, t will be I(1). The general approach is to obtain residuals from Equation (38.6) and then to test whether residuals are I(1) by running the auxiliary regression,
eit = |
rieit – 1 + uit |
(38.7) |
or |
|
|
|
pi |
|
eit = rieit – 1 |
+ Â wijDeit – j + vit |
(38.8) |
j = 1
for each cross-section. Pedroni describes various methods of constructing statistics for testing for null hypothesis of no cointegration (ri = 1 ). There are two alternative hypotheses: the homogenous alternative, (ri = r) < 1 for all i (which Pedroni terms the within-dimen- sion test or panel statistics test), and the heterogeneous alternative, ri < 1 for all i (also referred to as the between-dimension or group statistics test).
The Pedroni panel cointegration statistic ¿N, T is constructed from the residuals from either Equation (38.7) or Equation (38.8). A total of eleven statistics with varying degree of properties (size and power for different N and T ) are generated.
Pedroni shows that the standardized statistic is asymptotically normally distributed,
¿N, T – m N |
fi N(0, 1) |
(38.9) |
-------------------------------- |
 v
v
where m and v are Monte Carlo generated adjustment terms.
Details for these calculations are provided in the original papers.
Kao (Engle-Granger based) Cointegration Tests
The Kao test follows the same basic approach as the Pedroni tests, but specifies cross-sec- tion specific intercepts and homogeneous coefficients on the first-stage regressors.
In the bivariate case described in Kao (1999), we have
yit = ai + bxit + eit |
(38.10) |
for

702—Chapter 38. Cointegration Testing
yit |
= |
yit – 1 |
+ ui, t |
(38.11) |
xit |
= |
xit – 1 |
+ ei, t |
(38.12) |
for t = 1, º, T ; i = 1, º, N . More generally, we may consider running the first stage regression Equation (38.6), requiring the ai to be heterogeneous, bi to be homogeneous
across cross-sections, and setting all of the trend coefficients gi |
to zero. |
Kao then runs either the pooled auxiliary regression, |
|
eit = reit – 1 + vit |
(38.13) |
or the augmented version of the pooled specification, |
|
p |
|
˜ |
(38.14) |
eit = reit – 1 + Â wjDeit – j + vit |
j = 1
Under the null of no cointegration, Kao shows that following the statistics,
DFr = T--------------------N(r-------------– 1) ----------------+ 3 N- |
|
|||||||
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
10.2 |
|
|
||
DFt = |
|
1.25tr + |
1.875N |
|
||||
* |
|
|
ˆ |
1) + |
|
ˆ 2 |
ˆ 2 |
|
= |
NT(r – |
3 Njv § |
j0v |
|||||
DFr |
--------------------------------------------- |
3 + |
ˆ 4 |
ˆ |
4 --------- |
- |
||
|
|
|
|
|||||
|
|
|
36jv |
§ (5j0v) |
|
|||
* |
|
tr + 6Njv § (2jˆ 0v) |
|
|||||
DFt |
= |
|
|
ˆ |
|
|
|
|
ˆ 2 |
ˆ |
2 |
ˆ 2 |
ˆ 2 |
||||
|
|
|||||||
|
|
j 0 v |
§ (2jv ) + 3jv § |
(10j0v) |
||||
and for p > 0 (i.e. the augmented version), |
|
|
|
|||||
|
|
tr˜ + 6Njˆ v § (2j0v) |
|
|||||
ADF = |
|
|
|
|
ˆ |
|
||
2 |
ˆ 2 |
ˆ 2 |
|
ˆ 2 |
||||
|
|
|
||||||
|
|
j 0 v |
§ (2jv ) + |
3jv § |
(10j0v) |
|||
(38.15)
(38.16)
(38.17)
(38.18)
(38.19)
|
|
|
|
ˆ |
2 |
= |
ˆ 2 |
ˆ 2 |
–2 |
converge to N(0, 1) asymptotically, where the estimated variance is jv |
ju |
– jue je |
|||||||
ˆ 2 |
ˆ 2 |
|
ˆ 2 |
–2 |
|
|
|
|
|
with estimated long run variance j0v = |
j0u – j0ue j0e . |
|
|
|
|
|
|||
The covariance of |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wit |
= |
uit |
|
|
|
|
|
|
(38.20) |
|
|
eit |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
is estimated as
