
ЗФТШ_2013-2014_полное / ЗФТШ_2013-2014_полное / МАТЕМАТИКА / m9_1_планиметрия_I
.pdf
2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)
CMO ~ ANO MCAN = MONO , поэтому BMND = MCAN , т. е. vx = uy .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
РИС. 26 |
РИС. 27 |
|||||||||||||||||||
Перемножим полученные равенства, получим |
x2 |
= |
y2 |
, откуда следует |
|||||||||||||||||||
uv |
uv |
||||||||||||||||||||||
x = y , но тогда и u = v . ■ |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4° В равнобокой трапеции углы при основании равны.
□ Проведём CF 
 BA (рис. 26). ABCF − параллелограмм, CF = BA,
BA (рис. 26). ABCF − параллелограмм, CF = BA,
тогда треугольник FCD равнобедренный, 1 = 2. Но 2 = 3, сле-
довательно, 1 = 3. ■
5° В равнобокой трапеции высота, опущенная из конца меньшего основания на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой – полуразности оснований.
□ Если BM AD и CN AD, то |
BAM = CDN (рис. 27). |
||
MBCN −прямоугольник, MN =b , тогда ND = a −b , |
|
||
а AN = a − a −b |
= a +b . ■ |
2 |
|
|
|
||
2 |
2 |
|
|
6° В равнобокой трапеции прямая, проходящая |
|
||
через середины оснований, перпендикулярна ос- |
|
||
нованиям и является осью симметрии трапеции. |
|
||
□ Пусть K − точка пересечения продолжений бо- |
|
||
ковых сторон трапеции (рис. 28). Как следует из |
|
||
свойства 2o , середины оснований – точки M и N −и |
РИС. 28 |
||
|
|
|
|
© 2013, ЗФТШ МФТИ, Пиголкина Татьяна Сергеевна |
21 |
||
|
|
|
|
2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)
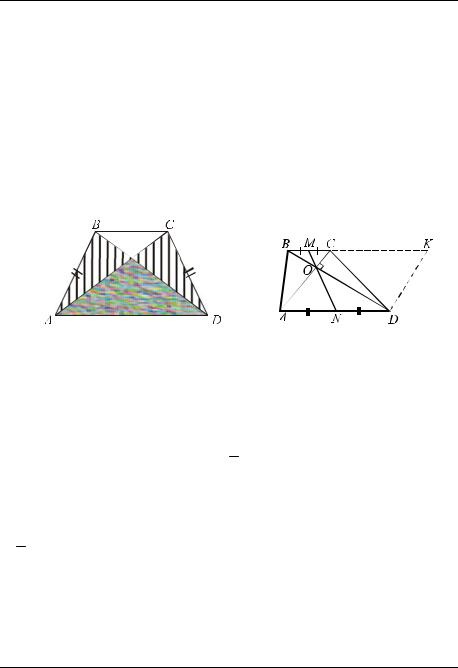
точка K лежат на одной прямой, а как следует из свойства 4o , углы A и D равны. Таким образом, треугольник AKD − равнобедренный, KN − его медиана, она является и высотой. Итак, MN AD.
Легко видеть, что при симметрии относительно прямой MN точки A и B переходят в точкаD и C и наоборот. MN − ось симметрии трапеции. ■
7° В равнобокой трапеции диагонали равны.
□ Рассмотрим треугольники ABD и DCA (рис. 29): AB = DC (трапеция равнобокая), AD − общая сторона, BAD =ADC (следует из
свойства 4°). По первому признаку равенства эти треугольники равны и
BD = AC. ■
РИС. 29 РИС. 30
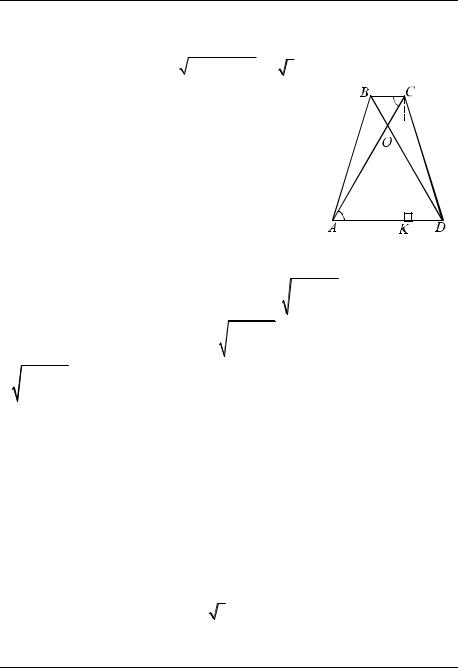
Пример 14. Диагонали трапеции перпендикулярны, одна из них равна 6. Отрезок, соединяющий середины оснований, равен 4,5 (рис. 30). Найти другую диагональ.
1. Треугольник AOD − прямоугольный, ON − медиана, проведённая из вершины прямого угла, она равна половине гипотенузы, т. е.
ON = 12 AD.
Аналогично устанавливается, что |
OM = |
1 |
BC . По свойству |
3° |
точки |
|
2 |
||||||
|
|
|
|
+ON = |
||
M , O и N лежат на одной прямой. Таким образом, MN =OM |
||||||
=12 ( AD +BC) , поэтому AD +BC =2MN =9 .
2.Проведём через точку D прямую, параллельную диагонали AC, пусть K − точка её пересечения с прямой BC . Угол BDK прямой, это угол между диагоналями трапеции. Кроме того, ACKD по построению параллелограмм, CK = AD , значит, BK = BC + AD =9 .
© 2013, ЗФТШ МФТИ, Пиголкина Татьяна Сергеевна
22
2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)
Треугольник BKD − прямоугольный, один из катетов (пусть DK ) равен 6 . По теореме Пифагора находим:
BD = BK 2 −DK 2 =3 5. ▲
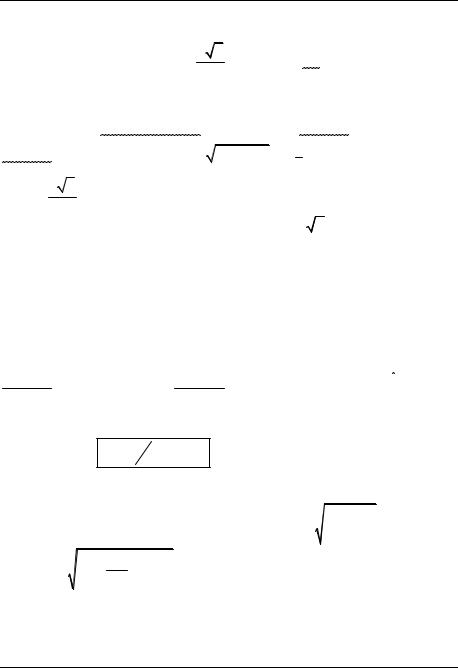
Пример 15. В равнобокой трапеции с периметром 10 и высотой 2 диагонали, пересекаясь, делятся в отношении 4 :1. Найти основания.
1. Пусть O −точка пересечения диагоналей |
|
|
|
|
|||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
трапеции ABCD (рис. 31) и |
AO : OC = 4 :1. Тре- |
|
|
|
|
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
угольники |
AOD |
и |
|
COB |
подобны, |
|
|
|
|
||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||
AO : OC = AD : BC = 4 , т. е. |
AD = 4BC . Обозна- |
|
|
|
|
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
чим BC = x , тогда AD = 4x . |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
2. |
Пусть CK AD; CK − высота трапеции, |
|
|
|
|
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
по |
условию |
CK = 2 , |
а |
как |
следует |
из |
|
|
|
|
|||||
свойства 5°, |
1 |
|
|
3 |
|
|
|
|
РИС. 31 |
||||||
KD = |
|
( AD − BC) = |
|
x . Из прямо- |
|
|
|
|
|||||||
2 |
2 |
9 |
|
|
|
||||||||||
угольного треугольника CKD имеем CD = |
4 + |
x2 . Выражаем пери- |
|||||||||||||
4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
метр |
трапеции: |
|
|
5x + 2 |
4 + 9 x2 |
|
|
Решаем |
уравнение |
||||||
10 = |
. |
|
|||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 4 + 9 x2 =10 −5x, |
оно |
имеет единственный |
корень |
x =1. Итак, |
|||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BC =1, AD = 4. ▲
Домашнее задание
Прежде чем приступать к нему, ознакомьтесь с нашими пожеланиями и требованиями.
1.За краткий ответ «да», «нет», «не может быть» без пояснений (доказательство, опровергающий пример) ставится 0 очков. Примеры ответов приведены далее.
2.Если в контрольном вопросе сначала требуется сформулировать или доказать некоторую теорему, то ответ на сопутствующий вопрос надо постараться дать на основе этой теоремы.
3.Если в решении длина какого-либо отрезка выразится иррацио-
нальным числом (например, a = 5 ), то ни в дальнейших вычислениях, ни в ответе не следует заменять это точное значение на приближённое.
© 2013, ЗФТШ МФТИ, Пиголкина Татьяна Сергеевна
23
2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)
4. Если в решении использовались тригонометрические функции и получилось, например, sinα = 2 32 , то не следует определять величину
угла α по таблице или на калькуляторе приближённо и затем тем же способом находить значение cosα, sin 2α, sin (α + 45o ) и т. п. Все значения других тригонометрических функций определяются только по
формулам! |
Например, |
cosα = − 1−sin2 α = − |
1 |
, |
если угол α тупой и |
|
|
2 2 |
|
|
3 |
|
|
sinα = |
, а |
|
|
|
|
|
|
3 |
|
|
|
|
|
( |
α +45o |
) |
=sinα cos 45o +cosα sin 45o = |
2 |
(sinα +cosα). |
sin |
|
2 |
5.Если в Задании контрольный вопрос сопровождается поясняющим рисунком, при ответе перенесите рисунок с теми же обозначениями в свою тетрадь, – это облегчит Вашему педагогу проверку работы.
6.Рисунок к задаче должен быть достаточно большим и ясным, чтобы на нём уместились все введённые Вами обозначения углов, отрезков
иданные задачи (посмотрите на рис. 12 и рис. 15 Задания: как хороший рисунок и обозначения помогают увидеть простое решение).
7.Стремитесь к тому, чтобы Ваше решение было кратким, но обос- нованным, и было ясным и понятным для проверяющего (работа проверяется без Вас, Вы не можете комментировать, что же имелось в виду). Для этого полезно решение разбивать на шаги: 1) … 2) … 3) … и то, что вычислено или выражено и важно для дальнейшего, выделять,
например, так AD = 3 2 x, BC =1.
Кроме того, вычисления разумно производить в кратких обозначениях (а математика – это здравый смысл), например
x |
|
u |
|
x |
|
y |
|
x = y и u =v или a = |
c |
|
|
|
|
= |
|
, |
|
= |
|
|
c |
|
−1 |
, |
|
y |
v |
v |
v |
|
2 |
|||||||
|
|
|
|
|
|
|
|
|||||
ане BC = AB AB −MN .
2
Примеры ответов на контрольные вопросы
Вопрос. Если в четырёхугольнике диагонали перпендикулярны, можно ли утверждать, что этот четырёхугольник – ромб?
© 2013, ЗФТШ МФТИ, Пиголкина Татьяна Сергеевна
24
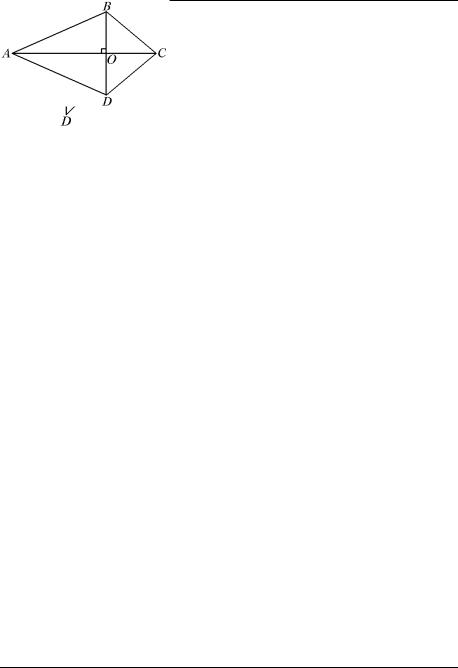
2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)
Ответ. Нет, нельзя. Например, четырёхугольник на рис. 32, в котором AC BD , ВО = OD и AO = 3OC ромбом не является, т. к. AB ≠ BC . Верным будет следующее утверждение: ели диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб.
РИС. 32 РИС. 33
Вопрос. Можно ли утверждать, что треугольник равнобедренный, если его биссектриса является медианой?
Ответ. Да, можно. Докажем это. Пусть в треугольнике ABC биссектриса ВМ является медианой: AM = МС (рис. 33). На продолжении биссектрисы ВМ отложим отрезок MD, равный ВМ. Треугольники АВМ и CDM равны по первому признаку: у них углы при вершине М равны,
как вертикальные, и AM = CM, ВМ = DM. |
|
Из равенства треугольников следует |
|
CD = АВ |
(1) |
и CDM =ABM . Но ABM = CBM , поэтому |
CDM =CBM , |
т. е. в треугольнике BCD углы при основании BD равны. По теореме этот треугольник равнобедренный: ВС = CD. Отсюда и из (1) заключаем: ВС = АВ. Утверждение доказано.
Контрольные вопросы
1(2). В прямоугольном треугольнике проекции катетов на гипотенузу ac и bc известны. Выразите через них c, a, b и h (именно в таком порядке по формулам §1) и найдите их при ac = 4; bc =5 .
2(3). Сформулируйте теорему, обратную теореме Пифагора. Как доказать, что она верна, не используя теоремы косинусов?
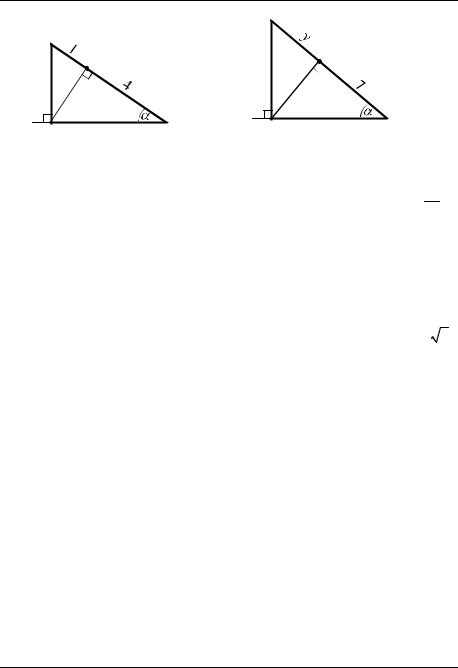
3(4). а) По данным рисунка 34 найдите x и cosα . б) По данным рисунка 35 найдите y и tgα.
© 2013, ЗФТШ МФТИ, Пиголкина Татьяна Сергеевна
25
2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)
x |
12 |
|
РИС. 34 |
РИС. 35 |
4(3). а) Существует |
ли прямоугольный треугольник, в котором |
a +b =17, r + R =9 ? |
|
б) Существует ли прямоугольный треугольник, в котором с = 254 и
hc =π ?
5(5). а) В каком отношении делится каждая медиана треугольника их общей точкой пересечения?
б) Как доказать, что ma + mb + mc > |
3 |
(a +b +c)? |
|
|
|
|
|||
|
4 |
|
|
|
в) Может ли быть ma =12, mc =9, c =10 ? |
|
|||
6(4). а) AA1 и CC1 − высоты треугольника ABC, AC =10, A1C1 =5 2 . |
||||
Чему равен угол ABC ? (Первая лемма о высотах) |
|
|||
б) Высоты AA1 |
и BB1 пересекаются в точке |
H , BH : HB1 =3: 2 , |
||
AH = y, HA1 = ky . |
При каком значении k угол |
ACB =60°? (Вторая |
||
лемма о высотах) |
|
|
|
|
7(5). а) В каком отношении биссектриса угла треугольника делит противолежащую этому углу сторону?
б) AD − биссектриса треугольника ABC, BD : DC =5 : 4 .
1)В каком отношении биссектриса AD делит медиану BM ?
2)В каком отношении медиана BM делит биссектрису AD ?
8(4). а) В трапеции ABCD углы при большем основании AD равны 35° и 55°. Чему равен отрезок, соединяющий середины оснований, если AD = 7 и BC =3 ?
б) Меньшее основание трапеции равно 3; отрезок с концами на боковых сторонах, параллельный основаниям и проходящий через точку пересечения диагоналей, равен 4. Чему равен отрезок, соединяющий середины диагоналей? (см. пример 4)
© 2013, ЗФТШ МФТИ, Пиголкина Татьяна Сергеевна
26

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)
9(4). а) В трапеции ABCD с основаниями AD = a, BC =b диагонали
AC и BD перпендикулярны друг другу. Чему равен отрезок соединяющий середины оснований? Какое свойство трапеции Вы используе-
те в ответе? |
|
|
|
|
3 C |
|
|
|
|
|||
б) Отрезок MN параллелен основаниям |
|
B |
|
|
|
|
||||||
трапеции |
ABCD (рис. 36), BC =3, |
AD =5 , |
|
|
|
|
|
x |
|
|
||
MN =3,5 . |
Чему равно отношение |
x : y ? |
M |
|
|
|
|
N |
|
|
||
|
3,5 |
|
|
|
||||||||
(см. пример 5) |
|
|
|
|
|
|
y |
|||||
|
|
|
|
|
|
|
|
|||||
10(5). а) Точка D лежит на стороне AB |
|
|
|
|
|
|
|
|
|
|||
треугольника ABC, точка K − на стороне |
A |
|
|
|
|
|
|
|
D |
|||
BC, |
AD : DB =3:1 и BK : KC = 4 :1. Прямая |
|
|
5 |
|
|
|
|||||
DK |
пересекает прямую AC в точке F . |
|
|
|
РИС. 36 |
|
|
|||||
Чему равно отношение CF : AC ?
б) При таком же расположении точек на сторонах треугольника отрезки AK и CD пересекаются в точке O . Чему равны отношения
AO : OK и DO : OC ?
Задачи
1(5). Окружность радиуса 2 вписана в прямоугольный треугольник ABC , в котором C =90° и BC =5 . Найти расстояние между цен-
трами вписанной и описанной окружностей.
2(8). Треугольник ABC равнобедренный AB = BC = 20, AC =32 . Найти расстояние от вершины B до
1)точки M пересечения медиан;
2)точки O1 пересечения биссектрис;
3)точки O пересечения серединных перпендикуляров сторон;
4)точки H пересечения высот.
3(5). Треугольник ABC − равнобедренный, AB = BC =5, AC = 4 . Найти периметр ортотреугольника (см. пример 7).
4(5). В прямоугольном треугольнике ABC ( C =90°) проведены высота CH , биссектриса CK и медиана CM .
1)Доказать, что CK делит пополам угол между CH и CM .
2)При HK =1 и KM = 2 найти: а) величину угла A; б) длину бис-
сектрисы CK; в) tg A .
© 2013, ЗФТШ МФТИ, Пиголкина Татьяна Сергеевна
27

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)
5(5). В трапеции |
ABCD боковая сторона AB перпендикулярна ос- |
нованиям и равна 6, |
а боковая сторона CD равна 61 . Диагонали тра- |
пеции перпендикулярны друг другу. Найти основания трапеции.
6(6). В треугольнике ABC медиана BM перпендикулярна биссек-
трисе AD, AB = 4, BM = 2 |
7 . Найти длины биссектрисы |
AD и сторо- |
|
ны BC . |
|
катета AC прямоугольного |
|
7(6). Через |
середину |
треугольника |
|
ABC ( C =90°) |
проведена прямая, пересекающая гипотенузу в точке |
||
D и продолжение катета BC в точке F . Известно, что AD = 2, CF =3
и ABC = 60°. Найти гипотенузу (два случая).
8(6). Медиана AM и биссектриса BD прямоугольного треугольни-
ка ABC ( C =90°) |
пересекаются в точке O, BO =9 |
и OD =5 . Найти |
||||
катеты и расстояние от точки O до гипотенузы AB . |
AD |
|
|
|||
9(6). Точка M − |
середина |
большего основания |
равнобокой |
|||
трапеции ABCD . |
Точка |
K |
лежит на стороне |
AB , |
при |
этом |
BK : KA =3: 2 . Основания |
трапеции AD =9 и BC = 4 . Прямая |
CK |
||||
перпендикулярна прямой BM . Найти высоту трапеции.
10(6). Биссектриса BD треугольника ABC делит сторону AC на отрезки AD =1 и DC = 2 . На прямой BD взята точка K (точка B ле-
жит между точками K и D ) так, что BK = 2 и AKC = 12 ABC .
1)Найти стороны AB и BC.
2)Найти cos( ABC).
11(4). Дан треугольник ABC . Биссектриса внешнего угла при вер-
шине A пересекает прямую BC в точке K . Доказать, что KCKB = ACAB .
© 2013, ЗФТШ МФТИ, Пиголкина Татьяна Сергеевна
28
