Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный физико-технический университет (МФТИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

m9_1_планиметрия_I

.pdf

Скачиваний:

575

Добавлен:

03.06.2015

Размер:

878.25 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)

Пример 4 (важное свойство трапеции). Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям,

пересекает боковые стороны трапеции в точках М и N. Найти длину отрезка MN, если основания трапеции равны a и b.

1. Пусть O − точка пересечения диагоналей, AD =a, BC =b. Пря-

мая MN параллельна основанию

AD (рис. 10а),

следовательно,

AD, треугольники BMO и BAD подобны, поэтому

(1)

Рис. 10 а)

Рис. 10 б)

2. AD

BC,

AOD COB по двум углам (рис. 10б):

то есть

3. Учитывая, что BD = BO +OD находим отношение

BO +OD

1+OD / BO

Подставляя это в (1), получаем MO =

; аналогично устанавливаем,

a +b

что ON =

, таким образом MN =

2ab

.▲

a +b

Пример 5. (полезный метод решения) Точки M и N лежат на бо-

ковых сторонах AB и CD

трапеции ABCD и MN

(рис. 11а). Найти длину

MN, если

BC =a, AD =5a,

AM : MB =1: 3.

1. Пусть BF CD и

ME CD

(рис. 11б), тогда

1 = 2,

3 = 4 (как

со-

а)

б)

Рис. 11

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)

ответствующие углы при пересечении двух параллельных прямых

третьей)	AE		AM	и	1	AME ~ MBF .
Из подобия следует		=		=		.
	MF		MB		3

2. Обозначим MN = x . По построению BCNF и MNDE − параллелограммы, FN = a, ED = x и, значит, MF = x −a; AE = 5a − x . Итак,

имеем 5xa−−ax = 13 , откуда находим x = 4a. ▲

Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон. Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.

Попытайтесь доказать это самостоятельно.

Признаки подобия прямоугольных треугольников

Прямоугольные треугольники подобны, если:

1)они имеют по равному острому углу;

2)катеты одного треугольника пропорциональны катетам другого;

3)гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.

Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.

Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения 1°, 2°, 3° можно доказать, используя подобие указанных треугольников.

Свойства высот и биссектрис Пример 6. (Первая лемма о высотах).


Если в треугольнике	ABC	нет прямого угла,	AA1	и	BB1 − его высо-

ты, то A1B1C ABC.
	(этот факт можно сформулировать так: если

соединить основания двух высот, то образуется треугольник, подобный данному).

□Как всегда, полагаем AB =c, BC = a, AC =b.

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)
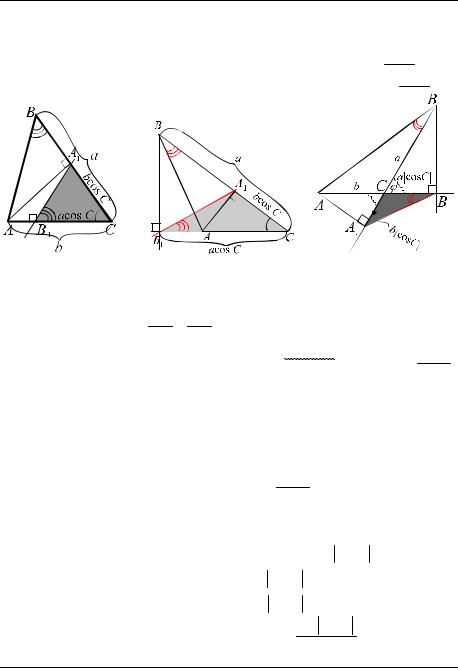
а) Треугольник ABC остроугольный (рис. 12а).
В треугольнике AA C угол A −прямой,						AC = AC cosC =b cosC.
				1	1	1
ВТРЕУГОЛЬНИКЕ BB1C УГОЛ B1 − ПРЯМОЙ, B1C = BC cosC = a cosC.
Рис. 12 а)					Рис. 12 б)		РИС. 12В
В треугольниках				A1B1C и ABC угол C общий, прилежащие сторо-
ны пропорциональны: A1C =					B1C =cosC.
				AC	BC
Таким образом,				A1B1C ABC с коэффициентом подобия cosC .
(Заметим, что A1B1C = B ).
б) Треугольник ABC − тупоугольный, угол C − острый, высота AA1
проведена из вершины тупого угла. Рассуждения аналогичны:
AA1C, A1 =90			o	A1C =

					AC cosC =bcosC;
BB C, B =90o
BB C, B =90o				B C = BC cosC = acosC,
	1	1		1
A1B1C ABC,				коэффициент подобия cosC ,			A1B1C = B.
Случай, когда угол B тупой, рассматривается аналогично.
в)	Треугольник		ABC − тупоугольный, угол C − тупой, высоты AA1
и BB1	проведены из вершин острых углов.
ϕ = BCB = ACA =180o					− C, cosϕ = −cosC = cosC .
		1		1
AA1C, A1 =90			o	A1C =	AC cosϕ =b cosC ;


BB C, B =90o				B C = BC cosϕ =b cosC ,
BB C, B =90o				B C = BC cosϕ =b cosC ,
	1	1		1

A1B1C ABC с коэффициентом подобияk = cosC ,
( A1B1C= B).■
© 2013, ЗФТШ МФТИ, Пиголкина Татьяна Сергеевна							13
							13

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)
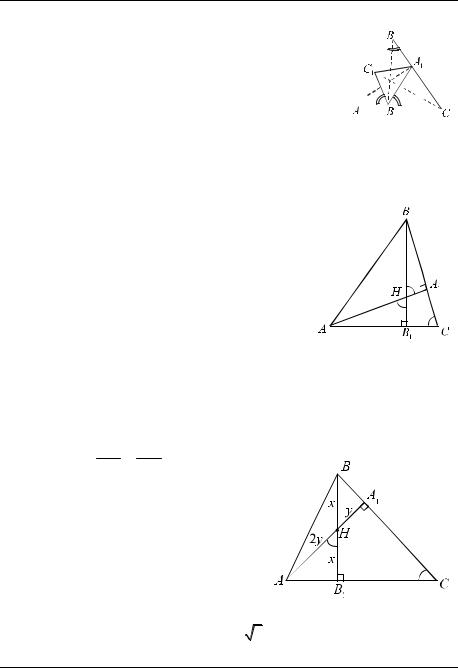
Пример 7. В остроугольном треугольнике АВС
проведены высоты				AA1 , BB1 , CC1 (рис. 13). Треуголь-
ник, вершинами которого служат основания высот,
называется «высотным» треугольником (или орто-
треугольником). Доказать, что лучи							A1 A, B1B и C1C
являются биссектрисами углов высотного треуголь-
ника	A1B1C1 (т. е. высоты остроугольного треуголь-								РИС. 13
ника являются биссектрисами ортотреугольника).
	По	первой		лемме		о высотах		A1 B1C ~	ABC, A1B1C = B.
Аналогично AB1C1 ~ ABC,						AB1C1 = B ,		т. е. A1B1C = AB1C1 .
Так как BB1 − высота, то
		AB1 B = CB1 B = 90°.
Поэтому C1B1B = A1B1B =90°− B , т. е.
луч B1B − биссектриса угла A1B1C1 . Аналогично
доказывается, что				A1 A −		биссектриса		угла
B1 A1C1 и C1C − биссектриса угла B1C1 A1 . ▲
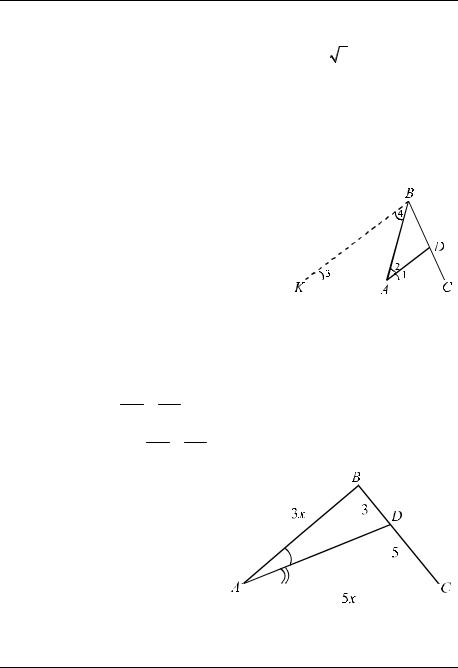
Пример 8. (Вторая лемма о высотах)
Высоты AA1 , BB1 треугольника ABC пере-									РИС. 14
секаются в точке				H	(рис.	14). Доказать,		что
имеет место равенство					AH HA1 = BH HB1 , т. е. произведение отрезков
одной высоты равно произведению отрезков другой высоты.
	AHB1 BHA1 , имеют по равному острому углу при вершине H
(заметим, что этот угол равен углу C ). Из подобия следует
		AH		= HB1 ,
		BH		HA
					1
откуда AH HA1 = BH HB1 . ▲
Пример 9. Высоты AA1						и BB1	тре-
угольника		ABC	пересекаются в				точ-
ке H , при этом BH = HB1 и						AH = 2HA1
(рис. 15). Найти величину угла C .
	1. По условию пересекаются высо-
ты, поэтому треугольник остроугольный.
Положим BH = HB1 = x и HA1 = y , тогда								РИС. 15
AH = 2 y .		По второй лемме о высотах
AH HA = BH HB				, т. е. x2 = 2 y2, x =y 2.
	1		1
© 2013, ЗФТШ МФТИ, Пиголкина Татьяна Сергеевна									14

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)

2. В треугольнике AHB1 угол AHB1 равен углу C (т. к. угол A1 AC

равен 90o −C ), поэтому cosC = cos( AHB1 )=	x	=	2	.
	2 y		2

Угол C − острый, C = 45o.

Ответ: C = 45o. ▲

Установим ещё одно свойство биссектрисы угла треугольника.

Теорема 5. Биссектриса внутреннего угла треугольника делит противолежащую этому углу сторону на отрезки, пропорциональ-

ные прилежащим сторонам, т. е. если AD −

биссектриса треуголь-

ника ABC, то

B прямую па-

□ Проведём через точку

раллельно биссектрисе DA,

пусть K − её

точка пересечения с прямой AC (рис. 16).

Параллельные прямые AD и KB пере-

сечены

прямой KC , образуются равные

углы 1

и 3. Те же прямые пересечены и

РИС. 16

прямой

AB , здесь равные углы 2 и 4. Но

AD − биссектриса, 1 = 2 , следовательно 3 = 4.

Отсюда следует, что треугольник KAB равнобедренный, KA = AB.

По теореме о пересечении сторон угла параллельными прямыми из

AD KB следует DCBD = ACKA . Подставляя сюда вместо KA равный ему

отрезок AB , получим DCBD = ACAB . Теорема доказана. ■

Пример 10. Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной 3 и 5. Найти в каких пределах может изменяться периметр треугольника.

Пусть	AD − биссектриса	и
BD =3,	DC =5 (рис. 17).	По
свойству	биссектрисы		РИС. 17
AB : AC =	3: 5 .		РИС. 17
AB : AC =	3: 5 .

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)

Положим AB =3x , тогда AC =5x . Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е.

5x < 3x +8, 3x <5x +8 и 8 < 3x +5x.

Получаем ограничения x < 4 и x >1. Периметр треугольника P =8 +8x =8(1 + x), поэтому 16 < P < 40. ▲

§ 4. Задачи о делении отрезка

Рассмотрим задачи, решения которых основаны на теореме о пресечении угла параллельными прямыми и подобии треугольников. Напомним теорему:

Теорема 6. Параллельные прямые, пересекая стороны угла, от- секают на них пропорциональные отрезки, т. е. если l1 l2 ,

AC = AC1 = CC1

AB AB1 BB1

или mx = mx ++yn = ny .

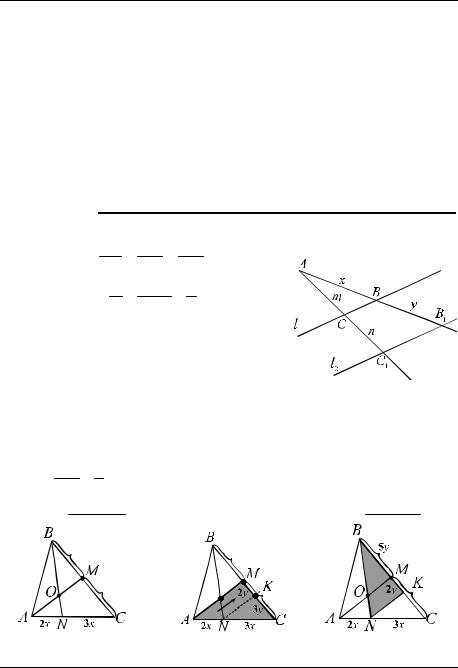
Пример 11. Точка N лежит на стороне

AC	треугольника	ABC ,	причём
AN : NC = 2 : 3 . Найти, в каком отношении
медиана AM делит отрезок BN.
1.	Пусть O − точка пересечения ме-
дианы	AM и отрезка	BN . Требуется найти отношениеBO : ON . Обо-

значим AN = 2x , тогда NC =3x . Отметим, что BM = MC (рис. 18а).

Проведём прямую NK параллельно медиане AM (рис. 18б). Парал-

лельные прямые AM и NK пересекают стороны угла MCA , следова-

тельно, MKKC = 23 .

Полагаем MK = 2 y, тогда KC =3y , а т. к. BM = MC , то BM =5y.

Рис. 18 а)

Рис. 18 б)

РИС. 18 В)

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)

2. Те же прямые пересекают стороны угла NBC (см. рис. 18в), по-

этому ONBO = MKBM = 52yy , т. е. ONBO = 52 ▲

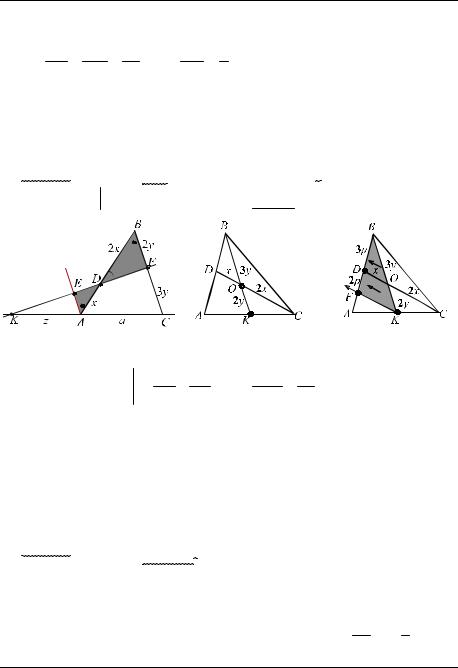
Пример 12. Точки D и F лежат на сторонах AB и BC треугольника ABC, при этом AD : DB =1: 2 и BF : FC = 2 : 3 .

Прямая DF пересекает прямую AC в точке K . Найти отношение

AK : AC .

1. Пусть AD = x, BF = 2 y, KA = z . Тогда DB = 2x и FC =3y .

Проводим прямую AE , параллельную стороне CB .

ADE BDF AE : BF = AD : BD AE = y.

РИС. 19

Рис. 20 а)

Рис. 20 б)

2.KAE KCF KCKA =CFAE , т. е. a +z z = 3yy . Находим a = 2z .

Ответ: AK : AC =1: 2. ▲

Пример 13. В треугольнике ABC точки D и K лежат соответственно на сторонах AB и AC, отрезки BK и CD пересекаются в точке O (рис. 20), при этом BO : OK =3 : 2 и CO : OD = 2 :1 . Найти в каком отношении точка K делит сторону AC, т. е. AK : KC .

1. Полагаем OD = x, OK = 2 y , тогда OC = 2x и BO =3y . Проводим прямую KF CD (рис. 20б).

Из KF OD ( ABK ) следует BD : DF =3: 2 . Обозначаем DF = 2 p , тогда BD =3p .

2.FBK DBO, FK : DO = FB : DB , откуда FK = 53 pp x = 53 x .

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)

AFK ADC, AF : AD = FK : DC .

Обозначаем AF = z , имеем

3 x

, откуда

z =

p , т. е. AF =

p .

z + 2 p

4. Рассматриваем BAC,

DC , по теореме AK : KC = AF : FP ,

т. е. AK : KC =5 : 4. ▲

Все три рассмотренные задачи могут быть решены с применением теоремы Менелая.

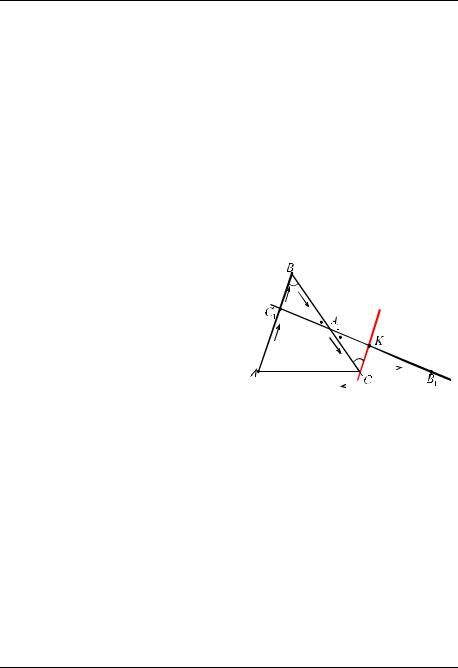
Теорема Менелая (о треугольнике и секущей).

Пусть точка

лежит на стороне BC, точка C1 − на стороне

AB , а точка B1 − на продолжении стороны AC за точку C .

Если точки A1 , B1 и C1 лежат на одной прямой (рис. 21), то вы-

полняется равенство

AC1

BA1

CB1

=1.

(*)

A C

C B

B A

Обратно, если выполняется равен-

ство (*), то точки A1 , B1 и C1

лежат

на одной прямой. (Заметим, что

можно считать B1C1 секущей тре-

угольника ABC, а

можно считать

BC секущей треугольника AB1C1 ).

РИС. 21

□ а)

Предположим, что точки

A1 , B1 и C1 лежат на одной прямой. Проведём CK

AB (рис. 21).

CKB1 AC1B1 , поэтому

CB1

, откуда CK =

CB1

AC1 .

CKA1 BC1 A1, значит

CA1

CB1

AC1

CA1

Подставляя сюда выражение для CK

, получим

, т. е.

AC1

BA1

CB1

=1, ч. т. д.

C B

A C

B A

РИС. 23

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)

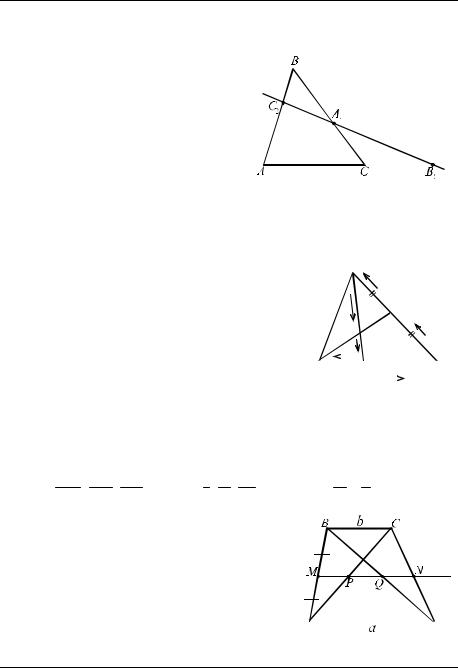
б) Пусть выполнено равенство (1) для точек								A1 , B1 и C1 (рис. 22),
докажем, что эти точки лежат на од-
ной прямой.
Через две точки A1 и B1 проведём
прямую, пусть C2 − её точка пересе-
чения с прямой AB (точка пересече-
ния будет лежать на отрезке AB ).
Три точки			A1 , B1		и C2 лежат на
одной прямой и по доказанному в

пункте а) выполняется равенство								РИС. 22
	AC2			BA1		CB1	=1.
				A C
	C	B				B A
2			1		1

Сравнив это равенство с равенством (*), придём к выводу, что

	AC2	=	AC1	. Точки C2 и C1 лежат на отрезке		B
		=		. Точки C2 и C1 лежат на отрезке		B
	C2 B C1B
	AB и делят его в одном отношении, считая от						m	M
конца A . Следовательно, точка C2					совпадает		m	M
конца A . Следовательно, точка C2					совпадает	O
с точкой C1 , т. е. точки A1 , B1 и C1					лежат на	O
с точкой C1 , т. е. точки A1 , B1 и C1					лежат на		n
одной прямой.							n		C
одной прямой.
	Стрелки на рисунке 21 (от точки A ) по- A					2x N		3x
	Стрелки на рисунке 21 (от точки A ) по- A					2x N		3x

казывают, как легко запомнить последовательность отрезков в пропорции (*). ■

Например, применим теорему Менелая задаче из примера 12. Полагаем BO = m, ON = n (см. рис. 23) и рассматриваем треугольник CBN

и секущую AM .

Имеем: CMBM ONBO ACNA =1 , т. е. 11 mn 52xx =1 , откуда mn = 52 .

§ 5. Трапеция

1° Во всякой трапеции середины боковых сторон и середины диагоналей лежат

на одной прямой.

□ Через точку M −середину стороны

AB − проведём прямую, параллельную осно-

ванию (рис. 24). Докажем, что она разделит

пополам обе диагонали и другую боковую

РИС. 24

2013-2014 уч. год, №1, 9 кл. Математика. Планиметрия (часть I)

сторону. В треугольнике BAC MP BC и AM = MB . По теореме Фале-

са AP = PC .

В треугольнике ABD точка M − середина стороны, MQ AD . Пo теореме Фалеса BQ =QD . Наконец, в треугольнике BDC точка Q − середина BD, QN BC . По теореме Фалеса CN = ND .

Итак, середины боковых сторон (точки M и N ) и середины диагоналей (точки P и Q) лежат на одной прямой.

2° Средняя линия трапеции равна полусумме оснований; отрезок, соединяющий середины диагоналей, равен полуразности оснований.

□ Пусть AD = a, BC =b . Из 1o следует, что MQ − средняя линия треугольника ABD, поэтому MQ = a2 ; MP и QN − средние линии тре-

угольников BAC и BDC , поэтому MP =QN = b2 . Отсюда следует, что

MN = a +2 b и PQ = a −2 b . ■

3° Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.

□ Пусть продолжения боковых сторон пересекаются в точке K . Через точку K и точку O пересечения диагоналей проведём прямую KO

(рис. 25).

Докажем, что эта прямая делит основания пополам.

Обозначим BM = x, MC = y,

AN =u, ND =v.

Имеем:

BKM

AKN

;

M C

x y

MKC

NKD

т. е.

Далее, BMO ~ DNO

РИС. 25

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в папке МАТЕМАТИКА

#
03.06.2015582.15 Кб489m8_1_тождественные_преобразования_уравнения.pdf
#
03.06.2015876.28 Кб644m8_2_геометрия.pdf
#
03.06.2015602.62 Кб486m8_3_системы_уравнений.pdf
#
03.06.2015324.85 Кб476m8_4_квадратные_корни.pdf
#
03.06.2015321.37 Кб474m8_5_квадратные_уравнения.pdf
#
03.06.2015878.25 Кб575m9_1_планиметрия_I.pdf
#
03.06.2015849.44 Кб487m9_2_квадратный_трёхчлен_иррациональные.pdf
#
03.06.2015454.98 Кб493m9_3_многочлены_модули_уравнения_неравенства.pdf
#
03.06.2015759.83 Кб493m9_4_планиметрия_II.pdf
#
03.06.2015429.37 Кб495m9_5_теория_множеств_логика.pdf
#
03.06.2015342.4 Кб584m9_6_элементы_комбинаторики_вероятность.pdf