m10_4_тригонометрические_функции_уравнения

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный физико-технический университет (МФТИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3 sin 2t sin

t в точке t

3 sin 2t sin

t в точке t

.pdf

Скачиваний:

488

Добавлен:

03.06.2015

Размер:

797.07 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «Заочная физико-техническая школа

Московского физико-технического института (государственного университета)»

МАТЕМАТИКА

Тригонометрические функции и уравнения

Задание №4 для 10-х классов

(2013 – 2014 учебный год)

г. Долгопрудный, 2013

2013-2014 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения

Составитель: С.И. Колесникова, старший преподаватель кафедры высшей математики МФТИ.

Математика: задание №4 для 10-х классов (2013 – 2014 учебный год), 2013, 26 с.

Дата отправления заданий по физике и математике – 4 февраля 2014 г.

Учащийся должен стараться выполнять все задачи и контрольные вопросы в заданиях. Некоторая часть теоретического материала, а также часть задач и контрольных вопросов, являются сложными и потребуют от учащегося больше усилий при изучении и решении. В целях повышения эффективности работы с материалом они обозначены символом «*» (звѐздочка). Мы рекомендуем приступать к этим задачам и контрольным вопросам в последнюю очередь, разобравшись вначале с более простыми.

Составитель:

Колесникова София Ильинична

Подписано в печать 20.12.13. Формат 60×90 1/16. Бумага типографская. Печать офсетная. Усл. печ. л. 1,75. Уч.-изд. л. 1,5. Тираж 550. Заказ №35-з.

Заочная физико-техническая школа Московского физико-технического института (государственного университета)

ООО «Печатный салон ШАНС»

Институтский пер., 9, г. Долгопрудный, Москов. обл., 141700, ЗФТШ, тел./факс (495) 408-51-45 – заочное отделение,

тел./факс (498) 744-63-51 – очно-заочное отделение, тел. (499) 755-55-80 – очное отделение.

e-mail: zftsh@mail.mipt.ru

Наш сайт: www.school.mipt.ru

2013, ЗФТШ МФТИ, Колесникова София Ильинична

Рис. 1

2013-2014 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения

I. Тригонометрические функции

Что главное в тригонометрии? Конечно, знание формул. Все они выводятся просто. Но почему-то не запоминаются. Здесь совет один – выучить их наизусть.

1. Синус угла – определение

Ясно,	что	точка		М на	произвольной		y
окружности с центром в начале координат

определяется однозначно двумя координа-								M
тами.							sin

Если задана окружность единичного ра-								A
диуса, то	координаты носят специальные								x
							O	cos
названия:	x это		косинус		угла	угла

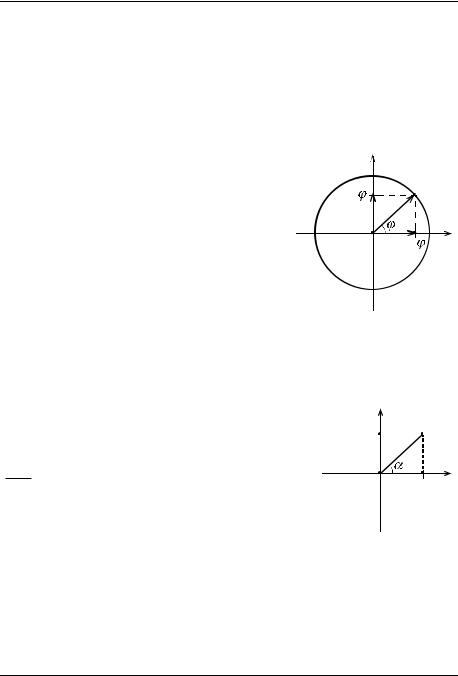
АОМ, а y синус этого угла – рис.1, т. е.

xcos , y sin .

Акак же треугольник? Посмотрим на

координаты точки М, находящейся в первой четверти.

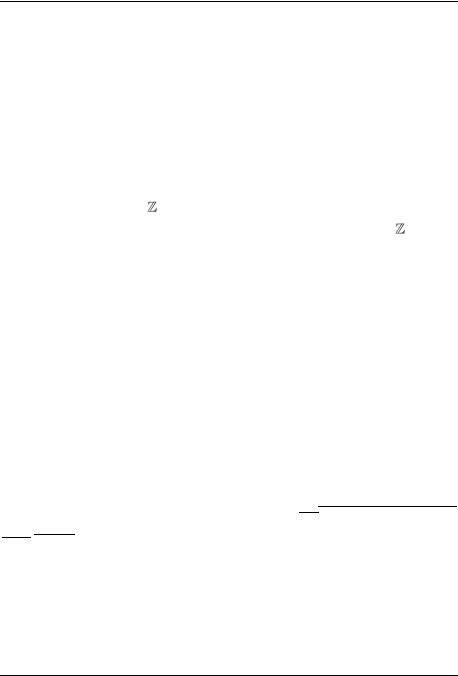
Отметим один из углов, синус которого равен OP, а косинус равен ON, острый угол . Этот угол находится в прямоугольном треугольнике NOM. Поэтому отношение противолежащего

катета к гипотенузе

sin MN OP y ,

а отношение прилежащего катета к гипотенузе

ON	cos ON x ,	т.	е.	новое	определение	O	N	x
OM

косинуса и синуса полностью совпадает со ста-
рым в прямоугольном треугольнике,
	sin		cos	Рис. 2

tg cos ,		ctg sin .

Итак, для любого		значения ; определены значения

sin , cos , т. е. определены тригонометрические функции

ysin , y cos .

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения

Отсюда, в частности, следует так называемое основное тригоно-

метрическое тождество:

cos2 sin2 1.

(1)

Это тождество применяется не только тогда, когда нужно связать синус и косинус одного аргумента, но иногда с его помощью неоднородное уравнение удаѐтся сделать однородным, заменив 1 суммой квадратов. Тогда говорят, что использовали «тригонометрическую» единицу.

На рис.1 угол изменяется от 0 до 2 , а ведь косинус и синус определены для любого угла. Координаты конца радиуса-вектора для

угла 0	и 0 2 k, k	, как видно, одинаковы:
	x cos 0 cos 0	2 k , y sin 0 sin 0 2 k , k .

Говорят, что поэтому функции cos и sin – периодические с периодом 2 .

2. Периодичность функции

Можно дать общее определение периодичности.

Определение. Функция f x называется периодической, если существует такое отличное от 0 число Т, для которого выполнены следующие два условия:

1)если x D( f ) , то x T D( f ) и x T D( f ) ;

2)для любого x D( f ) f (x) f (x T ) f (x T ) , т. е.

область определения периодична, а значения функции в точках, отстоящих друг от друга на длину периода, одинаковы.

Покажем, что, если функция имеет период T , то любое число вида nT , n Z – тоже период.

►Действительно, если T – период, то равенство f (x) f (x T )f (x T ) выполнено для любого x из области определения функции. В частности, выполнено для x T и x T :

f (x T ) f ( x T T ) f ( x T T ) f (x) f (x 2T ) f (x), f (x T ) f ( x T T ) f ( x T T ) f (x) f (x 2T ) f (x),

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения

т. е. для n 2 верно. По индукции доказывается и справедливость утверждения для любого n Z .◄

Поэтому, говоря о периоде функции, часто имеют в виду наименьший положительный (НПП) период, если таковой существует. Известно, что y sin x, y cos x определены на всей числовой оси и имеют

наименьший положительный период T 2 . Функции y tgx и y ctgx определены не на всей числовой оси. Однако их область определения является периодичной с периодом – это интервалы вида

и k; k , k соответственно.

Функции

y tgx, y ctgx имеют наименьший положительный период T .

Известно,

что

2 – период sin x , а какой наименьший период у

sin 3x ?

Покажем,

что, если число T является периодом функции

f x , то

число

является периодом функции g(x) f (ax).

► Действительно,

g x

f a x

f ax T f ax g x , т. е.

период функции g. ◄

Это важное свойство. Из него следует, например, что sin13x имеет пе-

риод, равный	2	, а	tg	17	x имеет период, равный	3	, и т. д.
	13			3		17

А существуют ли периодические функции, у которых нет наимень-

шего периода?				Да, такие тоже							есть. Например, функция
y x sin2		x	1		1	cos 2x		имеет наименьший период T				2	,
1		2		2							2
		2		2							2
функция	y	x cos2 x					1		1	cos 2x	имеет наименьший период
функция	y	x cos2 x								cos 2x	имеет наименьший период
	2			2				2
				2				2

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения

T	2	,	а их сумма y x sin2 x cos2 x не имеет наименьшего
	2

периода, т. к.			y sin2 x cos2 x 1, и еѐ периодом является любое по-

ложительное действительное число.

При построении графика периодической функции достаточно построить его на любом отрезке, длина которого равна длине наименьшего периода, а далее продолжить периодически, т. е. сдвигать график вдоль оси абсцисс на длину периода.

А что можно сказать о периодичности f (x) sin x ?

Область определения этой функции – полуось x 0 . Она не имеет периода: например, при любом T 0 число 0 принадлежит области определения, а число 0 T не принадлежит. Поэтому f (x) sin x не является периодической.

В школе, как правило, кроме стандартных тригонометрических, других периодических функций не встречается. Но мы всѐ-таки познакомимся с задачами, относящимся не только к тригонометрическим пери-

одическим функциям.
Пример 1.						Пусть		f x		–	периодическая функция с периодом
T	1	. Найти значение						f 1 , если известно, что
T		. Найти значение						f 1 , если известно, что
3
			2	0 5 f 0					21					2	1			10	35.
		f									0	и 4 f					4 f
		f									0	и 4 f					4 f
									4									3
					2			1						1		21
			f			0	3		5 f		0	3					0,
			f			0	3		5 f		0	3		3		4	0,
								3						3		4
►						2			1				10			1
			4 f			2	1	6	1				10		7	1	35
											4 f
											4 f
									3			3				3
									3			3				3

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения

							4 f		1 20 f 1 21 0,
4 f 2	1	20 f	1	21	0,			2
	1 4 f 1 35								1 56
4 f 2	1 4 f 1 35					16 f			1 56

4 f 2 1 20 f 1 21 0,

f 1 3,5

Ответ. 3,5. ◄

		3. Чѐтность функций
Определение. Функция			f x называется четной (нечетной) на X ,
если выполнено два условия:
1) если x X , то и x X ,
2)	для	любых	x X	выполнено	f ( x) f (x)
или f ( x) f (x) , т. е.			если, во-первых, область определения сим-

метрична относительно начала координат, а во-вторых, значения функции в симметричных точках равны (или f ( x) f (x) ).

Все остальные функции называются функциями общего вида на X . Отсюда сразу следует, что, если область определения функции не

является симметричной относительно 0, то функция не является ни чѐтной, ни нечѐтной, т. е. является функцией общего вида.

Если же функция рассматривается на множестве X , симметричном относительно 0, то надо проверить, выполняется ли условие 2).

Теперь можно понять, какими свойствами обладают графики чѐтных и нечѐтных функций.

Пусть функция задана для неотрицательных, например, y x, x 0 . Тогда, если отразим этот график симметрично относительно оси ординат, то получим график чѐтной функции – y x .

А если отразим этот же график симметрично относительно начала координат, то получим график нечѐтной функции – y x, x ; .

А можно хотя бы перечислить свойства таких функций? Конечно.

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения

1. Сумма или разность двух чѐтных (нечѐтных) функций, имеющих одну и ту же область определения, есть чѐтная (нечѐтная) функция.

2. Произведение или частное двух чѐтных или нечѐтных функций, имеющих одну и ту же область определения, есть чѐтная функция.

3. Произведение чѐтной и нечѐтной функций есть нечѐтная функция.

Любую функцию можно представить в виде суммы чѐтной и нечѐт-

ной функций.

f x можно построить две других – чѐт-

►По заданной функции

ную g x и нечѐтную h x :

g x

f x f x

g x

f x f x

g x .

h x

f x f x

h x

f x f x

h x .

Тогда

f x f x

f x g x h x

f x .◄

В школе мы привыкаем иметь дело лишь с тригонометрическими чѐтными или нечѐтными функциями, а сейчас порешаем задачи с произвольными чѐтными или нечѐтными функциями.

Пример 2. Определить, являются ли чѐтными, нечѐтными или функциями общего вида следующие функции:

а) (2) y

б) (2) y

cos 4x

x2 ,

Ответ. а) чѐтная; б) нечѐтная.

а) Функция y x2

– чѐтная, т. к.

б) Функция

cos 4x

является нечѐтной функцией, т. к. еѐ область

cos 4x

определения

( D

;0 0; )

симметрична

y x y x .

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения

4. Основные формулы тригонометрии. Формулы приведения

Самые простые формулы – это формулы для углов вида , ко-

гда все функции меняют только название – функция заменяется «кофункцией»: синус изменится на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.

		cos ,
sin		cos ,
	2

		ctg ,
tg	2

		sin ,
cos		sin ,
2
		tg .
ctg		tg .
2

Все остальные формулы сложнее – где-то меняется знак, где-то не меняется:

		cos ,
sin		cos ,
2
		ctg ,
tg		ctg ,
2


cos	sin ,
2
		tg .
ctg		tg .
2

sin sin ,	cos cos ,
sin sin ,	cos cos .

5. Множество значений функций Пример 3. Найдите значение функции

►Преобразуем заданные выражения, используя периодичность и формулы приведения:


		17				19		17							5
		17				19		17							5
3 sin	2			sin						3 sin				sin
3 sin	2			sin				3		3 sin			3	sin	6
			3			2		3					3		6
						sin
							sin		5		3	1	2.
					3				5	3	3	1
					3					3
					3				6		2	2

Ответ. 2 . ◄

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №4, 10 кл. Математика.

Тригонометрические функции и уравнения

6. Упрощение числовых тригонометрических выражений

Пример 4. Упростите выражение

sin

cos

► Применяем одну из формул приведения и используем основное три-

гонометрическое тождество:

cos

sin

1. .

sin

cos

Ответ. 1.◄

7. Обратные тригонометрические функции

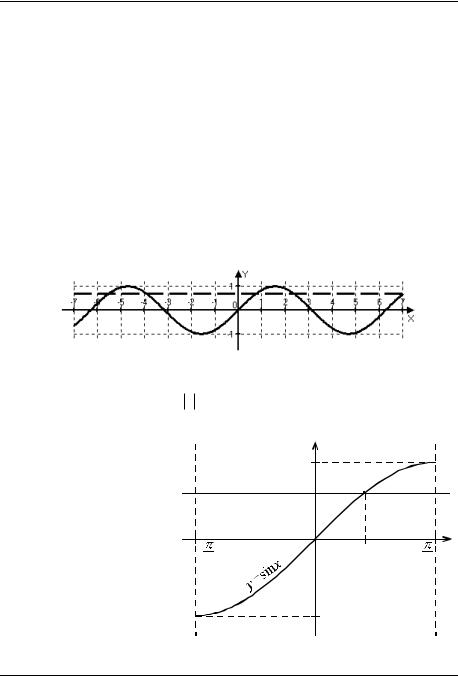
Всем известен график функции y sin x – так называемая

Рис. 3

синусоида – рис. 3.

Проведѐм прямую y a,

a 1.

Хорошо видно, что прямая пересекает график в бесконечном числе

точек, т. е.

уравнение

sin x a, a 1;1 имеет

бесконечно много

реше-

y=a

ний. Как описать это бес-

конечное множество

ре-

шений уравнения?

Рассмотрим

теперь

- 2

arcsina

y sin x не на всей чис-

ловой оси, а только на той

еѐ части, которая ближе

всего к x 0 и на кото-

-1

рой синус принимает все

Рис. 4

2013, ЗФТШ МФТИ, Колесникова София Ильинична

1 / 31 2 3 > Следующая >>>

Соседние файлы в папке МАТЕМАТИКА

#
03.06.2015691.07 Кб494m10_1_алгебраические_уравнения_неравенства.pdf
#
03.06.20151.06 Mб502m10_2_планиметрия.pdf
#
03.06.2015811.68 Кб495m10_3_последовательности_пределы.pdf
#
03.06.2015797.07 Кб488m10_4_тригонометрические_функции_уравнения.pdf
#
03.06.20151.15 Mб558m10_5_стереометрия.pdf
#
03.06.2015406.24 Кб497m10_6_комплексные_числа.pdf
#
03.06.2015836.96 Кб486m11_1_алгебраические_уравнения_неравенства_системы.pdf
#
03.06.2015633.52 Кб613m11_2_планиметрия.pdf
#
03.06.2015527.77 Кб492m11_3_тригонометрические_уравнения_системы.pdf