m11_1_алгебраические_уравнения_неравенства_системы

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный физико-технический университет (МФТИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1(2). Равносильны ли неравенства

.pdf

Скачиваний:

489

Добавлен:

03.06.2015

Размер:

836.96 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

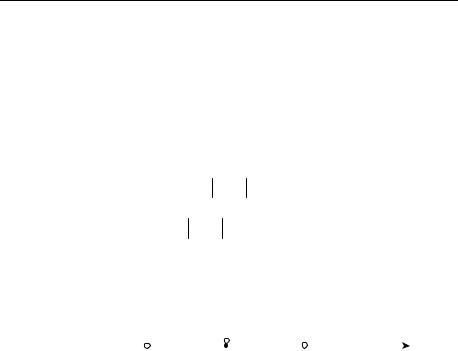
2013-2014 уч. год, №1, 11 кл. Математика.

Алгебраические уравнения, неравенства, системы уравнений и неравенств

И, наоборот: пусть

в некоторой точке

a выполнены

неравенства

g a f a g a .

Тогда, во-первых,

g a g a g a 0 , а,

во-вторых,

f a

g a . Следовательно, имеет место условие равно-

сильности

f x g x ,

f x

g x g x f x g x

(УР М1)

f x g x .

п.2. Неравенство вида f x g x .

Пусть в некоторой точке a неравенство выполнено, т. е. f x g x .

Это означает, что, или,

а) g a 0 (модуль принимает неотрицательные значения и всегда больше любого отрицательного числа), или,

б) если g x 0 , имеет место картинка

f (a)

g(a)

Рис. 7

f a

g a ,

и совокупность неравенств

g a .

f a

И, наоборот, пусть в некоторой точке a имеет место совокупность

неравенств f a g a ,

Тогда,

f a g a .

f a

g a выполнено,

а) если g a 0 , то неравенство

б) если g a 0 , то имеет место предыдущая картинка и выполне-

но неравенство

f a

g a .

Следовательно, имеем равносильные соотношения

f x

f x g x ,

g x

(УР М2)

f x g x .

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №1, 11 кл. Математика.

Алгебраические уравнения, неравенства, системы уравнений и неравенств

Пример 14. (МГУ, 2000, ВМК) Решите неравенство x2 8x 2 x2 2x 2.

8x 2

x2 2x 2,

x2 8x 2

2x 2

8x 2

x2 2x 2

8x 2 x2 2x 2,

8x 2

2x 2;

x2 8x 2 x2

8x 2

x2 2x 2

8x 2 x2

2x 2,

8x 2 x

2x 2

x 0,

x 1;2 , 2,

x ;0 1;2 5; .

, 3;2 ,

x ;0 5;

Ответ: ;0 1;2 5; .

f x

g x

п.3. Неравенство вида

Рассмотрим разность

f x

g x

. Она может быть любого знака,

но сумма

f x

g x

всегда неотрицательна,

и умножение разности

на эту сумму не изменит знака разности, т. е.

f x g x f x g x

f x 2 g x 2 f 2 x g 2 x f x g x f x g x и

знак разности

f x

g x

совпадает со знаком

произведения f x g x f x g x

(П М1)

Имеем

еще одно условие равносильности

f x

g x

f x g x f x g x 0 .

(УР М3)

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №1, 11 кл. Математика.

Алгебраические уравнения, неравенства, системы уравнений и неравенств

Пример 15. (МФТИ, 2000)

Решите неравенство

x2 7x 6

x2 6x 5

x2 2x 3

ОДЗ*: x2 7x 6 0 x 1 x 6 0 x 1;6 .

В ОДЗ* имеем

x2 7x 6

(в силу УРМ3)

6x 5

x2 2x

x2 7x 6

2x2 8x 2 4x 8

x 2

x2 7x 6 0,

x 1,

x 2 3,

x 6,

x 2,


x 2		x 2		x 2 0	2	3; 2 2	3; .
x 2	3	x 2	3	x 2 0	2	3; 2 2	3; .

Учитывая ОДЗ*, получаем

Рис. 8

Ответ: 1;2 2 3;6 .

§4. Системы уравнений

1.Самым распространенным методом решений систем является метод последовательного исключения неизвестных: выражаем одно неизвестное из одного из уравнений и подставляем в остальные. Получаем новую систему, в которой число уравнений и неизвестных на одно меньше. С новой системой поступаем так же до тех пор, пока это возможно.

Однако очень часто при решении системы этим способом мы приходим к уравнениям, которые невозможно решить. Общих правил для решения систем не существует, но для некоторых систем существуют специальные приемы.

2.Однородные системы

3.Симметрические системы

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №1, 11 кл. Математика.

Алгебраические уравнения, неравенства, системы уравнений и неравенств

4. Часто систему можно решить, если еѐ сначала упростить с помощью равносильных преобразований.

Приведем примеры некоторых преобразований, приводящих к равносильным системам.

1.Если любое уравнение системы заменить равносильным ему уравнением, то получим равносильную систему.

2.Если в одном из уравнений системы левая часть является произведением двух функций, то система равносильна совокупности при условии, что справа 0. Например,

				f			x, y 0,
					1
f	x, y f		x, y 0,
f	x, y f	2	x, y 0,	g x, y 0.
1		2					(УР С1)
							(УР С1)
g x, y		0			f	2	x, y 0
						2

				g x, y 0.

3.Если какое-нибудь уравнение системы умножить на число, отличное от нуля, то получится система, равносильная исходной. (УР С3)

4.Если к одному из уравнений системы прибавить линейную ком-

бинацию

нескольких других, то получим

равносильную систему.

x, y 0,

x, y af

x, y

Например,

(УР С2)

x, y

x, y 0,

a произвольное число.

x, y

x, y ,

x, y g x, y 0,

2 x, y g 2 x, y ,

x, y

x, y g

x, y

x, y 0,

g1 x, y 0,

2 x, y g2 x, y ;

(УРС3)

x, y g

x, y 0,

2 x, y g 2 x, y ,

x, y g

x, y .

Обратим внимание на то, что в равносильной системе появилось дополнительное неравенство! (т. к. возведение в квадрат не всегда приводит к равносильному уравнению.)

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №1, 11 кл. Математика.

Алгебраические уравнения, неравенства, системы уравнений и неравенств

					f
							1
	f		x, y g	x, y ,
6.	f		x, y g	x, y ,	f			2
6.	1		1
			x, y g2 x, y			f
	f	2	x, y g2 x, y			f
							1

					f			2

x, y g1 x, y 0,

x, y g2 x, y ;

(УР С4)

x, y g1 x, y 0,

x, y f1 x, y g2 x, y g1 x, y .

Обратим внимание на то, что в системе остается то уравнение, в ко-

тором обе части отличны от нуля!

f x, y 0,

x, y g x, y 0,

(УР С5)

g x, y 0

x, y g x, y

т. к.

f x, y 0,

x, y

g x, y 0,

g x, y 0

g x, y

x, y g x, y 0,

x, y g x, y 2g x, y 0

x, y g x, y 0.

2x2 y z 3,

Пример 16. Решите систему уравнений

y z 2x 1,

Выразим y

x4 yz y 2z 3.

из второго уравнения

y 1 z 2x , подставим в пер-

вое и третье и получим систему с двумя неизвестными

2x2 1 z 2x

z 3,

2x 2z 2,

x4 z 1 z 2x

1 z 2x 2z

x4 2zx 2x z2 2z 2.

z x2 x 1 и, подставив во

Теперь выразим из первого уравнения

второе, получим уравнение с одним неизвестным

x4 2x

x2 x 1

x 1

x2 1 0 x 1 z 1 y 2,

x 1 z 1 y 0.

Ответ: (1;2;1), (–1;0;–1).

x 2 y 3z 9,

Пример 17. Решите систему уравнений x2 4 y2

9z2 189,

3xz 4 y

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №1, 11 кл. Математика.

Алгебраические уравнения, неравенства, системы уравнений и неравенств

Выразим x из первого уравнения и подставим во второе и третье уравнения. Тогда получим равносильную систему

x 2 y 3z 9,

4 y2 9z2 6 yz 27z 18y 546 yz 9z2 27z 4 y2 0.

Теперь прибавим ко второму уравнению третье


x 2 y 3z 9,			y 3, z 4 x 3;
	y 3,		y 3, z 4 x 3;
18y 54	y 3,			x 12.
		5 3	y 3, z 1	x 12.
18z 9z2	27z 36 0 z	5 3
18z 9z2	27z 36 0 z
		2

Ответ: 3, 3, 4 , 12, 3,1 .

Пример 18. (МФТИ, 1996) Решите систему уравнений

x2 2xy 8y2 9x 30 y 8 0,

x2 6xy 8y2 2x 8 0.

В данной системе будем рассматривать каждое уравнение как квадратное относительно, например, x . Так как дискриминанты обоих уравнений являются полными квадратами, оказывается возможным свести систему двух нелинейных уравнений к совокупности четырѐх линейных систем.

x2	2xy 8y2 9x 30 y 8 x2 x 2 y 9 8y2 30 y 8 0,

	6xy 8y2 2x 8 x2 2x 3y 1
x2	6xy 8y2 2x 8 x2 2x 3y 1				8 8y2 0

		2 y 9 6 y 7		x 2 y 8 x 4 y 1 0,
	x
	x	2
		2
		3y 1 y 3
		3y 1 y 3	x 2 y		2 x 4 y 4 0
	x
	x	1
		1

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №1, 11 кл. Математика.

Алгебраические уравнения, неравенства, системы уравнений и неравенств

x 2 y

8 0,

x 5,

2 y

2 0;

;

x 2 y

8 0,

x 4,

4 y

4 0;

4 y

1 0,

2 y

2 0;

x 3,

4 y

1 0,

;

4 y 4 0.

Ответ: 5;

, 4; 2

, 3;

Пример 19. (МФТИ, 1999) Решите систему уравнений

4x 4 y 27 0,

2x 8y 10 0.

4x 4 y 27 0,

2x 8y 10 0.

Заменим второе уравнение системы суммой

4x 4 y 27 0,

4x 4 y 27 y2 2x 8y 10 0

x2 4x 4 y 27 0,

4 1 4 6 27 0,

x 1,

y 6

x 1

y 6

Заметим, что решение второго уравнения – это ещѐ не решение си-

стемы. Полученные числа необходимо подставить в оставшееся первое уравнение системы. В данном случае после подстановки получаем тождество.

Ответ: (1, – 6).
§5. Однородные уравнения и системы
Функция f x, y	называется однородной степени k ,	если
f tx,ty tk f x, y .	Например, функция f x, y 4x3 y 5xy3	x2 y2

является однородной степени 4, т. к. f tx,ty 4 tx 3 ty 5 tx ty 3

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №1, 11 кл. Математика.

Алгебраические уравнения, неравенства, системы уравнений и неравенств

tx 2 ty 2 t4 4x3 y 5xy3 x2 y2 . Уравнение f x, y 0, где f x, y –

однородная функция, называется однородным. Оно сводится к уравне-

нию с одним неизвестным, если ввести новую переменную t

f x, y a,

Система с двумя переменными

, где

f x, y , g x, y –

g x, y b

однородные функции одной и той же степени, называется однородной.

Если ab

0 , умножим первое уравнение на b, второе – на a и вы-

чтем одно из другого – получим равносильную систему

bf x, y ag x, y 0,

g x, y b.

Первое уравнение заменой переменных t

(или t

) сведѐтся к

уравнению с одним неизвестным.

Если

a 0

b 0 ,

то уравнение f x, y 0 g x, y 0 заменой

переменных t

(или

) сведѐтся к уравнению с одним неизвест-

ным.

xy y2 21,

Пример 20. (МГУ, 2001, химфак) Решите систему

2xy 15 0.

xy y

21,

x2 xy y2

2xy

2xy 15

x 0, y 0;

19 11

19xy 12 y

12 0

2xy 15

3y,

3 3,

2 3;

x 4,

y 5.

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №1, 11 кл. Математика.

Алгебраические уравнения, неравенства, системы уравнений и неравенств

Ответ: 33; 3 , 33; 3 , 4; 5 , 4; 5 .

§6. Симметрические системы
Функция f x, y называется симметрической, если				f x, y f y, x .
	f x, y a
Система уравнений вида		, где	f x, y , g x, y – симмет-
Система уравнений вида	g x, y b	, где	f x, y , g x, y – симмет-

рические, называется симметрической системой. Такие системы реша-

ются чаще всего с помощью введения новых переменных x y u, xy v.

x3 x3 y3 y3 17,

Пример 21. Решите систему уравнений

x xy y 5.

Эта алгебраическая (симметрическая) система, обычно она решается заменой x y u, xy v . Заметив, что

x3 x3 y3 y3 x y x2 xy y2 x3 y3

x y x y 2 3xy x3 y3 u u2 3v v3 ,

перепишем систему в виде

u	3	3uv	v	3	17,	u 5 v,		v 2,u 3,
u		3uv	v		17,			v 2,u 3,
u v 5						v2	5v 6 0	v 3,u 2

(в старых переменных)

x y 2,	x 2 y,
					.
xy 3,	y2		2 y 3	0
	x 3 y,				x 2, y 1,
x y 3,
		2
	y 3y 2 0				x 1, y 2.
xy 2,
Ответ: 2;1 , 1; 2 .

▲ Для успешного выполнения задания необходимо помнить, что строго монотонная функция любое своѐ значение принимает только

один раз, т.	е. если функция y x строго монотонна, то для любых
x* D y ,	x ** D y следует, что y x * y x ** x* x **.

Вспомним ещѐ свойства не просто монотонных функций, а нечётных монотонных.

2013, ЗФТШ МФТИ, Колесникова София Ильинична

2013-2014 уч. год, №1, 11 кл. Математика.

Алгебраические уравнения, неравенства, системы уравнений и неравенств

Если функция нечѐтная, то при любом x из области определения

f x f x f x f x 0, т. е. функция в симметричных

точках принимает «противоположные» значения.

случае

произвольной

нечѐтной

функции

равен-

ство f x1 f x2 может выполняться в нескольких точках (не толь-

ко

симметричных):

например,

sin

Если же функция нечётная, а к тому же и

-x0

x0 x

строго монотонная, то равенство

f x1 f x2 0 выполняется только в сим-

-a

метричных точках – вспомним график функ-

ции y x3

– рис. 9.

Рис. 9

Итак, если

f x нечётная и строго монотонная функция, то

f x1 f x2 f x1 f x2 0 x2 x1.

Поэтому для такой функции

f x :

f x f g x 0 x g x .

Контрольные вопросы

6 x

x 3

2(2). Равносильно ли неравенство

системе нера-

6 x

x 3

6 x 0,

венств

x 3

1 6 x ?

Решите неравенства 3 – 5 с помощью графиков и уравнений

3(2).

x 2 x 4.

4(3).

17 x 1 3x

x 3.

5(3). Решите уравнение 7 31x 10 x2 x 1 7 2x 4 .

2013, ЗФТШ МФТИ, Колесникова София Ильинична

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в папке МАТЕМАТИКА

#
03.06.20151.06 Mб509m10_2_планиметрия.pdf
#
03.06.2015811.68 Кб500m10_3_последовательности_пределы.pdf
#
03.06.2015797.07 Кб494m10_4_тригонометрические_функции_уравнения.pdf
#
03.06.20151.15 Mб566m10_5_стереометрия.pdf
#
03.06.2015406.24 Кб502m10_6_комплексные_числа.pdf
#
03.06.2015836.96 Кб489m11_1_алгебраические_уравнения_неравенства_системы.pdf
#
03.06.2015633.52 Кб616m11_2_планиметрия.pdf
#
03.06.2015527.77 Кб495m11_3_тригонометрические_уравнения_системы.pdf
#
03.06.2015739.63 Кб509m11_4_показательные_логарифмические.pdf
#
03.06.20151.13 Mб499m11_5_стереометрия.pdf
#
03.06.2015398.3 Кб492m11_6_теория_чисел.pdf