Квантовая химия каталитических реакций

Квантовая химия не предлагает принципиально новых методов для изучения гомогенного катализа, отличных от описанных выше. Некоторая специфика, тем не менее, существует. Она связана с тем, входит или нет молекула катализатора в переходное состояние химической реакции. В первом случае речь идет о наиболее эффективных разновидностях гомогенного катализа, например о таутомерном бифункциональном катализе. Необходимо рассчитать супермолекулу, состоящую из молекул исходных веществ и молекулы катализатора во всех особых точках ППЭ. При этом особое внимание следует уделять тому, к каким изменениям энергетических характеристик и индексов реакционной способности привело измененние структуры переходного состояния, пред- и послереакционных комплексов химической реакции в результате катализа. Учет каталитического влияния растворителя и твердотельной матрицы, когда их молекулы не входят в переходное состояние химической реакции, описан выше.

Квантовая химия каталитических реакций

Квантовая химия не предлагает принципиально новых методов для изучения гомогенного катализа, отличных от описанных выше. Некоторая специфика, тем не менее, существует. Она связана с тем, входит или нет молекула катализатора в переходное состояние химической реакции. В первом случае речь идет о наиболее эффективных разновидностях гомогенного катализа, например о таутомерном бифункциональном катализе. Необходимо рассчитать супермолекулу, состоящую из молекул исходных веществ и молекулы катализатора во всех особых точках ППЭ. При этом особое внимание следует уделять тому, к каким изменениям энергетических характеристик и индексов реакционной способности привело измененние структуры переходного состояния, пред- и послереакционных комплексов химической реакции в результате катализа. Учет каталитического влияния растворителя и твердотельной матрицы, когда их молекулы не входят в переходное состояние химической реакции, описан выше.

5 Электронная структура твердых тел

Твердое тело можно рассматривать как очень большую молекулу, в которой соблюдается либо дальний (идеальный), либо ближний порядок расположения атомов или молекул. Первый случай отвечает идеально регулярным кристаллам, симметрия которых описывается 230 федоровскими пространственными группами. Второй, более общий случай, охватывает реальные кристаллы с дефектами кристаллической решетки, аморфные тела, полимеры и т.д.: для них характерна лишь локальная симметрия определенных фрагментов. Для каждого из упомянутых случаев существуют свои способы описания электронной структуры. Идеально регулярные кристаллы считаются бесконечными (наличие поверхности игнорируется) и их волновые функции определяются с явным учетом трансляционной симметрии кристалла. В кристаллах с ближним порядком часто достаточно использовать модифицированные молекулярные модели, выделив некоторый атомный или молекулярный фрагмент – кластер. Рассмотрим оба этих подхода подробнее.

Одноэлектронные волновые функции в бесконечных периодических кристаллах и методы их расчета

Симметрийные свойства идеальных кристаллов состоят в следующем. В идеальном кристалле всегда можно ввести три вектора трансляций: ,и так, что физические свойства кристалла в некоторой произвольно выбранной точкеточно воспроизводятся в любой другой точкеудовлетворяющей условию:

(5.1)

где n_{1, n2, n3} - произвольные целые числа. Совокупность точек , определяемая выражением (5.1), при различных n_{1, n2, n3} дает кристаллическую решетку, которая описывает регулярное периодическое расположение точек в пространстве.

Параллелепипед, имеющий в качестве ребер вектора , и , называется элементарной ячейкой (рис.5.1). Перемещение всего кристалла как целого параллельно самому себе, описываемое вектором ,называетсятрансляцией. Вектор трансляции кристаллической решетки связывает любые две точки ре-шетки. (5.2)

Посредством соответствующих операций трансляций элементарной ячейкой можно заполнить все пространство кристаллической структуры. Такое свойство кристалла названо трансляционной симметрией. На рис.5.2 представлены структуры некоторых атомных и молекулярных кристаллов.

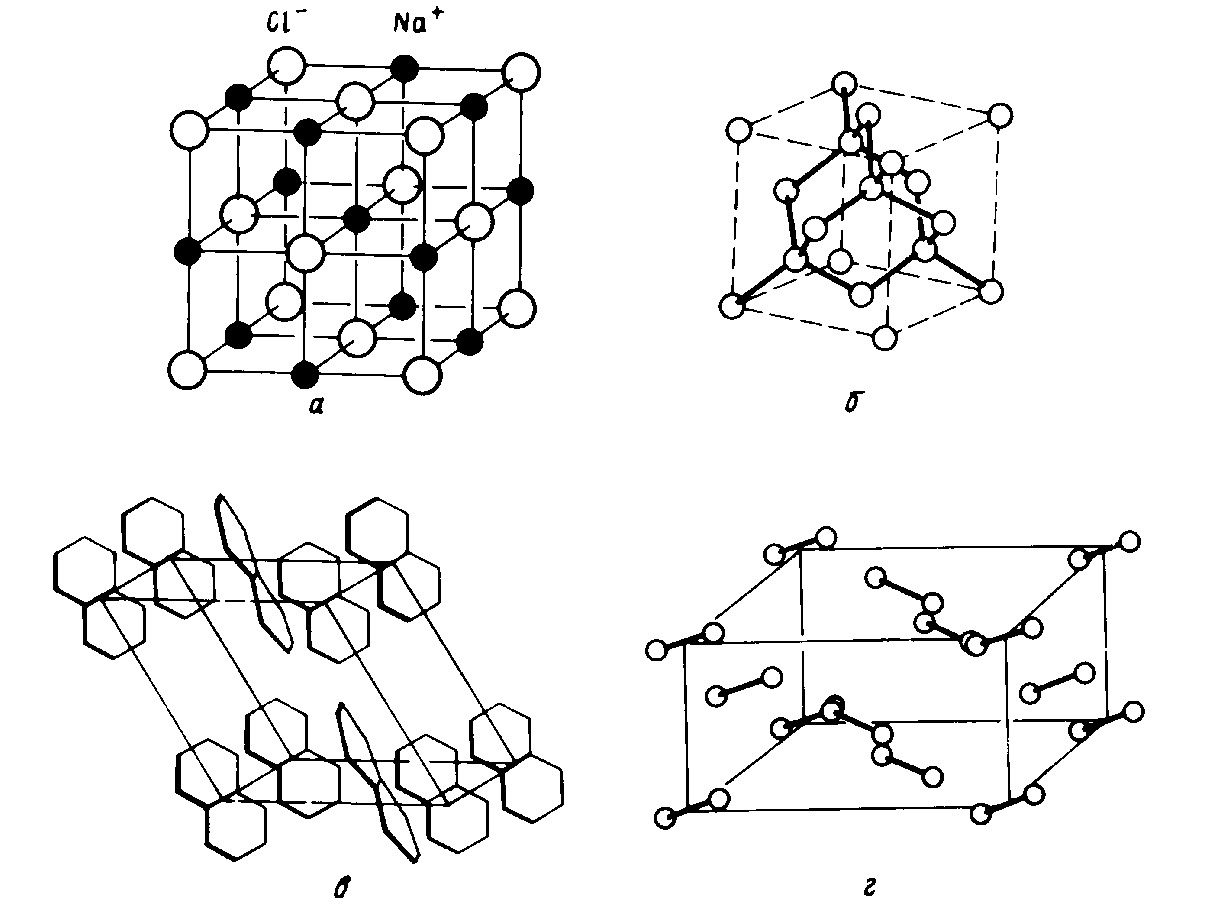
Рис.5.2. Кристаллические структуры NaCl(а), алмаза (б), нафталина и I₂ (г).

Трансляционная симметрия предполагает бесконечную протяженность кристалла. Конечно, регулярные структуры не являются бесконечными, а при отсутствии бесконечности теряется важное свойство трансляционной симметрии.

Один из способов сохранения трансляционной симметрии конечных систем - наложение циклических граничных условий (условия Борна-фон-Кармана). Суть их в том, что эквивалентные группы атомов отождествляются друг с другом так, чтобы граница отсутствовала.

Важнейшие электронные свойства периодических кристаллов хорошо видны уже в случае одномерных систем. Для цепочки атомов это равносильно изгибу цепочки в окружность большого радиуса и соединение между собой концевых атомов. Рассмотрим цепочку, состоящую из атомов, разделенных расстоянием а и имеющих один валентный электрон (Li, Na, K и т.д.), описываемый атомной орбиталью  (х). Каждое ядро в этих атомах хорошо экранировано внутренними электронами и валентный электрон лишь слабо связан со “своим” остовом. Влияние соседних атомом в цепочке приводит к тому, что валентные электроны могут передвигаться от атома к атому, как если бы они были свободными (модель почти свободных электронов Зоммерфельда). Волновая функция свободного электрона есть бегущая волна exp(ikx), а его кинетическая энергия равна

Е_кин= p²/2m=(kh)²/8²m, (5.3)

(k=2 /- волновое число или квазиимпульс электрона). Специфика нашей задачи состоит в том, что движение электрона происходит в слабом периодическом потенциале, вид которого обусловлен сортом и расположением атомов в решетке. Это означает, что потенциал V(x) в уравнении Шредингера

[T(x) + V(x)] u_k(x) = Eu_k(x) (5.4)

обладает свойством V(x)=V(x+na), где n=0,1, 2, … Учет этого обстоятельства при решении уравнения Шредингера приводит к тому, что волновая функция электрона в периодическом потенциале u_k(x) имеет вид модулированной зависящей от волнового числа k бегущей волны

u_k(x)=N _n exp(ikan) ( x + na) (5.5)

(N – нормировочный множитель), которая также периодична в решетке: (x) = (x+na) и сдвиг цепочки на величину, кратную а, не меняет u_k. Функция u_k, играющая в твердом теле роль атомной орбитали, называется функцией Блоха. При k =  b /a волновые функции электрона уже не являются бегущими волнами типа exp( ikx). Так, при b=0 k=0 и

u₀(x)=N [ ( x )+ ( x + a)+  (x + 2a)+  (x + 3a) +…], (5.6)

а при b=1 k=   /a и

u_/a (x)=N [ ( x )- ( x + a)+  (x + 2a)-  (x + 3a) +…] (5.7)

(см. рис5.3). В первом случае АО на разных атомах интерферируют в фазе и результирующая функция Блоха является связывающей и отвечает более низкой энергии. Второй случай отвечает деструктивной интерференции АО и,

a) k = 0 u₀ = N [  (x) +  (x + a) +  ....]

б) k = + /a u_/a = N [  (a) -  (x + a) +  .....]

Рис.5.3.

соответственно, - разрыхляющей функции Блоха. Таким образом, волновые функции электрона в периодическом потенциале можно ассоциировать со стоячими волнами вида u_1=sinx/a и u_{2 =cos}x/a, каждая из которых есть сумма бегущих волн (рис.5.4). Эти стоячие волны имеют узлы и пучности в разных областях пространства по отношению к создающим внешний потенциал атомным остовам. Это значит, что они отвечают концентрации электронов (которая пропорциональна u²) в местах, отвечающих различным значениям потенциальной энергии. Так, u₂ описывает концентрации электронов вблизи остовов, где потенциальная энергия минимальна, а u₁ - между остовами.

Число возможных значений k определяется числом узлов кристаллической решетки. Область в k –пространстве, лежащая между  /a, называется первой зоной Бриллюэна. Поведение электронов в более высоких зонах Бриллюэна

Рис.5.4.

получено из информации о первой зоне (рис.5.5). В пределах первой зоны Бриллюэна энергия по-прежнему имеет вид, близкий к (2). Однако на границах зон Бриллюэна среди возможных (“разрешенных”) значений энергии появляются разрывы из-за того, что средняя потенциальная энергия электрона, описываемого функцией u₂ меньше, чем для случая u₁. Разность энергий E_g называется энергетической щелью.

Кристаллические орбитали – аналоги МО – строятся из функций Блоха (4), которые таким образом играют в кристалле роль базисных функций:

_k (r ) =  c_j(k) u_kj(r) (5.8)

Таким образом, электроны в кристалле оказываются распределенными по энергетическим полосам (зонам), состоящим из уровней энергии, отвечающих волнам с разрешенными симметрией волновыми векторами. Расстояния между энергетическими уровнями на краях зоны меньше, чем в середине, т.е. плотность уровней (число уровней на единицу энергии) не одинакова по всей зоне: у краев зоны плотность выше. Для описания зависимости расстояния между уровнями от k предполагают непрерывное заполнение зоны (полосы) энергетическими уровнями и вводят непрерывную функцию Е(k), которую называют также структурой полосы. Она описывает закон дисперсии энергии. Высшая орбиталь в твердом теле, заполненная электронами, называется уровнем Ферми.

Распределение энергетических уровней в зоне характеризует плотность состояний:

D(E) = dN(E)/dE. (5.9)

Рис.5.5.

Интегрирование D(E) по dE до уровня Ферми дает полное число кристаллических орбиталей.

Разность между высшим и низшим энергетическими уровнями называют шириной зоны (полосы), она также характеризует дисперсию энергии. Ширина зоны определяется величиной взаимодействия между атомами в соседних ячейках и зависит от соответствующих интегралов перекрывания АО.

Промежуток между верхней энергетической зоной, заполненной элект-ронами (валентной), и нижней, не заполненной электронами (зоной проводи-мости) называется запрещенной зоной.

Рис. 5.6.

От того, как заполнена валентная зона и какова ширина запрещенной зоны, зависят многие свойства веществ. Зона Бриллюэна содержит столько разрешенных значений k- векторов (а значит, столько различных волновых функций), сколько элементарных ячеек N в кристалле. Если кристалл образовался из

атомов с g валентными электронами (g=1 для s оболочки; g=3 для p оболочки и т.д.), то зона состоит из Ng энергетических уровней, каждый из которых может быть занят 1 или 2 электронами (рис5.6). Если валентная зона полностью запол-нена электронами, а ширина запрещенной зоны Е_g2 эВ, то вещество называется диэлектриком. Если валентная зона полностью заполнена электронами, а ширина запрещенной зоны Е_g2 эВ, то вещество называется полупроводником. Если валентная зона заполнена электронами частично, либо перекрывается с зоной проводимости, то вещество называется металлом.

Рис.5.7.

Для расчета одноэлектронных волновых функций в кристаллах используют два основных метода.

1. Метод Хартри-Фока. Функции (5.5) используются как базисные и строятся из атомных орбиталей (как правиоло, ОСТ). Недостатки: из-за учета только корреляции Паули переоценивает ширину запрещенной зоны в 1.5-2 раза; неприменим для расчета Ферми-поверхности металлов.

2. Метод Кона-Шэма – относится к группе методов функционала плотности. Основан на предположении, что электронную плотность можно рассматривать как неоднородный электронный газ, определяющий обменно-корреляционные эффекты. Одноэлектронные уравнения имеют вид (атомные единицы):

[ -1/2² + V_N(r) + (r)/(r- r)dr+V_xc ] _k (r ) = E(k)_k (r ), (5.10)

здесь V_N –потенциал ядер, V_xc – обменно-корреляционный потенциал, для которого используются различные приближения – функционалы ЭП. Базисные функции различны: это могут быть как комбинации атомных орбиталей, так и наборы плоских волн. Недостаток: недооценка ширины запрещенной зоны.