2.22. Метод Парризера-Попла-Парра

Объединение нулевого дифференциального перекрывания и  -электронного приближения приводит к методу Парризера-Попла-Парра, дающего прекрасные результаты для  -электронных систем. Матричные элементы оператора Фока для этого метода приведены в табл. 2.16. U _ равно потенциалу ионизации атома в соответствующем валентном состоянии, взятому с обратным знаком: - I . Одноцентровые кулоновские интегралы   _ оцениваются по формуле Паризера-Парра (2.66). Величины I и A , необходимые для расчета U _ и   _ определяют из спектроскопических данных для валентных состояний атомов, используя модель локализованных связей. Двухцентровые интегралы  _AB рассчитывают по формулам (2.67)-(2.68). Величины h  считаются параметрами и выбираются по разному для расчета свойств основного (метод Попла) и возбужденных (метод Парризера-Парра) состояний.

1. Для основного состояния h  являются резонансными интегралами    = kS  , где k подбирается так, чтобы наилучшим образом воспроизводить теплоты образования в представительном круге соединений (существует и ряд других параметризаций).

2) Для возбужденных состояний следует учесть, что волновая функция молекулы должна быть суммой волновых функций основного  ₀ и возбужденных  _{i k} состояний:  = ₀ +  а_{i k i k}. Обычно учитывают несколько однократно возбужденных электронных конфигураций заданной мультиплетности и ищут коэффициенты а_{i k} вариационным методом. Матричные элементы ( _0 h   ₀) дают энергию основного состояния Е₀, а элементы ( _{i k} h   _{j l}) имеют вид:

( _{i k} h   _{j l}) h _{i k, j l} =  _{kl k} -  _{ij i} +2(jk li)-(jk  il). (2.70)

В приближении НДП

h _{i k, j l} =  _ij  _kl ( _k -  _i) + [2(1-R)с _j с _l c _i с _k - с _j с _i с _k c _l], (2.71)

где R=0 для синглетных состояний и R=1 – для триплетных.

Расчет проводится методом ССП, причем вначале определяют МО для основного состояния, а затем, используя их, строят волновые функции возбужденных состояний.

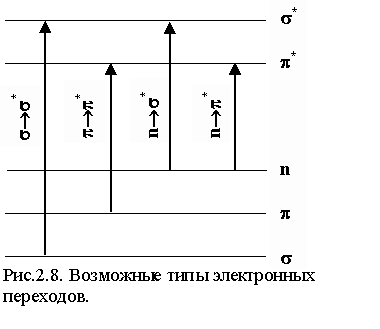
Метод Парризера-Попла-Парра включает в себя метод КВ и очень хорошо зарекомендовал себя как при определении геометрии, потенциалов ионизации и сродства к электрону, так и при расчетах оптических спектров поглощения сопряженных органических молекул. Спектр поглощения состоит из нескольких полос, связанных с определенными электронными переходами. Для плоских молекул МО можно разделить на три группы:  ,  и n^* . Наболее вероятное относительное расположение соответствующих энергетических уровней и разрешенные правилами отбора типы электронных переходов показаны на рис. 2.8. Диагонализизация матрицы h _{i k, j l} называемой матрицей конфигурационного взаимодействия, дает энергии спектральных переходов и веса возбужденных конфигураций а_{i k}. Ориентированный на  -электроны, метод ППП хорошо описывает  - ^* переходы (рис. 2.9.): точность оценки синглет-синглетных переходов составляет 0,1-0,2 эВ или 3-5% .

Интенсивность полосы поглощения f определяется квадратом дипольного момента перехода и равна f =К    а_{i k} c _i с _k x ². Она оценивается методом ППП с ошибкой 40-50%.