2.2 Приближение Борна-Оппенгеймера
Из-за наличия электрон-ядерного взаимодействия Vэя, пренебречь которым нельзя (см. таблицу 2.1), гамильтониан (2.2) не разделяется на ядерную и электронную части. Такое разделение может быть, однако, реализовано приближенно, если сделать зависимость электронной волновой функции эл от ядерной конфигурации R параметрической (приближение Борна-Оппенгеймера). Для этого запишем молекулярную волновую функцию в виде произведения электронной и ядерной компонент ({r, R}) = эл({r,R})яд({R}); заметим, что отлична от в (2.1). Соответствующее уравнение Шредингера имеет вид:
Н ({r, R})=Е ({r, R}), (2.3)
а электронная волновая функция удовлетворяет электронному уравнению Шредингера вида:
Нэ эл= Еэл эл, (2.4)
где
Рассмотрим теперь члены, описывающие кинетические энергии электронов и ядер:
В жестких молекулах ядра лишь совершают малые колебания относительно равновесных положений, тогда как электроны делокализованы по всей молекуле. Это означает, что в стабильной молекуле эл является медленно меняющейся функцией ядерных координат R и ее первой и второй производной по этим координатам можно пренебречь. Отбрасывая соответствующие члены в (2.6 б) перепишем уравнение Шредингера (2.3) в виде:
Примем теперь во внимание (2.4) и (2.5) и запишем:
Деля это уравнение на эл , получаем уравнение для определения яд:
Таким образом, электронная энергия Еэл, являющаяся суммой энергии движения электронов в поле фиксированных ядер и энергии ядерного взаимодействия, играет роль потенциальной энергии в уравнении Шредингера, описывающем движение ядер. Рассчитывая Еэл для разных значений, получим потенциальную поверхность энергии, вдоль которой ядра движутся в энергетическом пространстве. Поэтому Еэл называется адиабатическим потенциалом. Полная энергия молекулы в приближении Борна-Оппенгеймера есть сумма Е = Еэл + Тя, где Тя есть колебательно-вращательная энергия ядер.
Обоснованность приближения Борна-Оппенгеймера обусловлена тем фактом, что отношение масс электрона и ядра не меньше, чем 1/1836. Поэтому движение ядерной подсистемы происходит много медленнее, чем электронной и для большинства задач ядерную конфигурацию можно считать фиксированной. Ядерная конфигурация, которая становится в принятом приближении вполне определенным понятием, стабильна относительно малых колебаний ядер. Она характеризует молекулярную структуру. Такая картина несправедлива, однако, если энергия ядерных колебаний ниже, чем разность энергий основного и возбужденных электронных состояний. При этом возникают так называемые вибронные состояния, а адиабатический потенциал теряет свой ясный физический смысл. Следствием этого является, в частности, важный структурный эффект Яна-Теллера, который будет рассмотрен позже.
2.3 Метод Хартри-Фока для молекул
В рамках приближения Борна-Оппенгеймера для анализа электронного поведения молекул достаточно рассматривать только электронное уравнение Шредингера (2.4) для выбранной ядерной конфигурации. Получить его точное решение для многоэлектронной молекулы, а тем более для кристалла невозможно и для этой цели используются приближения, введенные в квантовой химии атома, и прежде всего - метод Хартри-Фока.
В методе Хартри-Фока для молекул детерминант Слейтера (1.48), являющийся приближением к N-электронной волновой функции молекулы, составляется из занятых электронами молекулярных орбиталей (МО) i( x ):
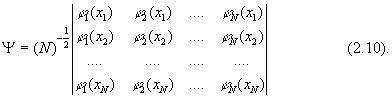
Каждая МО описывает поведение одного электрона в поле остальных электронов и (в отличие от атома!) всех ядер системы. Ясно, что концепция МО тесно связана с теорией многоэлектронного атома. Подобно АО, МО зависит от координат лишь одного электрона (является одноэлектронной) и записывается в виде произведения пространственной i(x) и спиновой (s) компонент: i(x)= i(x) (s). Каждая МО характеризуется своим значением энергии i, которая является собственным значением оператора Фока молекулы: электроны заполняют МО в порядке повышения энергии молекулы. Полная ХФ энергия молекулы с замкнутыми оболочками определяется соотношением, аналогичным выражению (1.55) в теории атома, а именно:
Последний член здесь описывает электростатическую энергию отталкивания ядер. Остальные члены имеют тот же смысл, что и в теории атома.
В минимизации энергии участвуют только занятые электронами МО, следовательно лишь они являются найденными физически обоснованно. Однако метод ХФ дает и характеристики свободных МО, которые соответствуют возбужденным энергетическим уровням молекулы лишь с большой ошибкой (около 100%). Такие МО называются виртуальными; применять их для трактовки спектроскопических данных следует с осторожностью – для этого существуют другие методы (см. ниже).
В дополнение к ХФ энергии, для оптимизации геометрии молекулы (если она известна лишь приближенно) и определения частот гармонических коле-баний ядер, вычисляются первые и вторые производные полной энергии относительно ядерных координат. Раньше производные рассчитывали методом конечных разностей; сейчас это делают непосредственным аналитическим дифференцированием выражения (2.11), что точнее. Минимум полной энергии соответствует наилучшей геометрии молекулы, а диагонализация матрицы вторых производных, являющихся силовыми постоянными молекулы, дает частоты нормальных колебаний. Кроме того, стационарные точки энергетической потенциальной поверхности (точки, где первые производные энергии по ядерным координатам обращаются в нуль) могут быть минимумом, максимумом или седловой точкой. Анализируя расположение и типы точек, можно охарактеризовать превращения молекул в ходе химических реакций. Мы вернемся далее к этой важной проблеме.
Полную сводку соответствующих аналитических формул можно найти в книге Y.Yamaguchi, Y.Osamura, J.D. Goddard, H.F.Schaffer III. A New Dimentions to Quantum Chemistry: Analytic Derivative Methods in Ab Initio Molecular Electronic Structure Theory. Oxford Univ.Press, N-Y, 1994. -471p.