
МИФИ
.pdf
Чтобы найти период колебаний, найдем возвращающую силу. Пусть смещение перемычки от положения равновесия равно x , а токи через источники в этом положении равны I1 и I2 (см. рису-
нок). Тогда, поскольку напряжение на концах перемычки в любой момент времени равно нулю, по закону Ома для участка цепи между А и В через источник ε имеем:
ε − I12ρ((L / 3) − |
|
x) = 0 |
или |
I1 = |
|
|
|
|
ε |
|
. |
(4) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2ρ((L / 3) − |
x) |
||||||||||||||||||
|
|
|
|
|
|
|
A |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
ε |
|
|
|
|
|
i |
|
|
B |
|
|
|
|
|
|
I2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
2ε |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
B |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично для тока через второй источник получим
I2 = |
2ε |
|
2ρ((2L / 3) +Δx). |
(5) |
Из формул (4), (5) находим ток через перемычку
i = I − I |
|
= |
ε |
|
3 x |
≈ |
27ε |
x |
(6) |
|
2ρ ((L / 3) − x)((2L / 3) + x) |
4ρL2 |
|||||||
1 |
2 |
|
|
|
|
||||
(в последнем приближенном равенстве использована малость отклонения перемычки от положения равновесия по сравнению с длиной рельсов). Из формулы (6) следует, что сила Ампера, действующая на перемычку со стороны магнитного поля,
F =iBl = |
27εBl |
x |
(7) |
|
4ρL2 |
||||
|
|
|
пропорциональна смещению перемычки, и, следовательно, перемычка будет совершать гармонические колебания с периодом
T = 2π 4mρL2 .
27Blε
50
|
|
|
г. Балаково, апрель 2009 г. |
|
||
1. Из закона сохране- |
y |
υ1 |
||||
ния импульса в проекциях |
|
|||||
на оси, |
одна из которых |
|
m |
|||
направлена вдоль началь- |
υ |
|||||
|
||||||
ной скорости первого те- |
|
|||||
|
5m |
|||||
ла, вторая – |
перпендику- |
m |
||||
лярно (см. рисунок), име- |
α |
|||||
|
||||||
ем |
|
|
|
|
υ2 |
|
mυ =5mυ2 cos α; |
|
|
||||
|
υ |
|
(1) |
|
x |
|
m |
|
=5mυ2 sin α. |
|
|
||
2 |
|
|
||||
|
|
|
|
|
||
Возводя уравнения в квадрат и складывая, получаем уравнение, в которое не входит угол α. Решение этого уравнения относительно неизвестной скорости второго тела дает
υ2 = 105 υ.
Если же разделить второе уравнение системы (1) на первое, получится уравнение относительно тангенса α, решение которого есть
α= arctg 1 .
2
2.См. решение задачи 2 из Олимпиады памяти И.В. Савельева.
3.См. решение задачи 2 из заключительного тура от 9 апреля
2009 г., г. Москва.
4.Исследуем условия равновесия системы поршней, связанных стержнем. Для этой системы внешними силами являются: силы,
действующие на поршни со стороны газа между ними Fг,1 и Fг,2 , и
со стороны внешнего атмосферного воздуха Fa,1 и Fa,2 |
(см. рису- |
нок). Условие равновесия поршней дает |
|
Fг,1 + FGг,2 + FGa,1 + FGa,2 = 0 |
(1) |
или |
|
pS1 − pa S1 + pa S2 − pS2 = 0 , |
(2) |
51 |
|

где p – давление газа между поршнями. Из формулы (2) получаем
|
p(S2 − S1 )= pa (S2 − S1 ). |
(3) |
|||||
Fг,1 |
|
|
|
|
|
|
|
|
|
Fа,1 |
Fа,2 |
|
|
Fг,2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку площадь труб различна, т.е. S1 ≠ S2 , из формулы (3) следует, что давление газа между поршнями равно атмосферному p = pa . (Если бы трубы были одинаковы, то условие (3) выполня-
лось бы благодаря равенству нулю скобки (S2 − S1 ) в правой и ле-
вой частях равенства (3), а давление газа между поршнями могло бы быть любым.) При нагревании или охлаждении газа между поршнями давление газа должно остаться равным атмосферному (иначе нарушаются условия равновесия), и, следовательно, процесс, происходящий с газом между поршнями, является изобарическим. Это значит, что при нагревании газа между поршнями объем газа между ними должен возрасти, поршни сместятся вправо, при охлаждении поршни сместятся влево. Поскольку при смещении поршня вправо до стыка труб объем газа станет равен 2S2l (l – рас-
стояние от поршня до стыка в начальном состоянии), а в начальном состоянии он равен S1l + S2l , по закону Гей-Люссака
S1l + S2l = 2S2l T0 T1
находим искомую температуру газа
T1 = 2S+2T0 . S1 S2
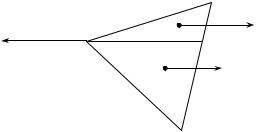
5. Поскольку треугольник перемещают равномерно, то внешняя сила F, которая перемещает треугольник, равна суммарной силе трения:
52
F =μ1m1g +μ2m2 g , |
(1) |
где m1 и m2 – массы частей треугольника, находящихся над первой и второй полуплоскостью (см. рисунок, эти части обозначены, как ABD и ACD). Из-за разности коэффициентов трения треугольник будет располагаться несимметрично относительно границы полуплоскостей, и потому массы m1 и m2 заранее нам неизвестны. Однако одно утверждение относительно этих масс довольно очевидно. Поскольку высоты треугольников ABD и ACD, опущенные из вершины A, одинаковы, их площади, а следовательно, и массы относятся так же, как и длины их оснований
|
|
|
m1 |
= |
BD |
. |
|
|
|
(2) |
|
|
|
m |
|
|
|
||||
|
|
|
|
CD |
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
μ1 |
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
F1 |
= μ1m1g |
|
G |
|
|
|
|
|
|
|||
|
F |
A |
|
|
l1 |
|
D |
|
||
|
|
|
|
|
||||||
|
|
|
|
|
l2 |
|
|
F2 = μ2m2 g |
||
|
|
μ2 |
|
|
|
|
|
|
|
|
C
Найдем теперь массы m1 и m2 треугольников ABD и ACD. Для этого заметим, что поскольку треугольник движется равномерно, то и сумма моментов всех действующих на него сил относительно любой точки равна нулю. В частности, должна быть равна нулю сумма моментов сил трения относительно той вершины, к которой приложена внешняя сила F. Моменты сил трения можно вычислить из следующих соображений. Треугольник движется поступательно, поэтому силы трения, действующие на любые малые элементы треугольника, направлены противоположно силе F и пропорциональны массам этих элементов. Поэтому моменты сил трения можно вычислять так же, как и момент силы тяжести, действующей на протяженное тело – приложить суммарную силу трения, действующую на части треугольника к их центрам тяжести. На рисунке
53
центры тяжести треугольников ABD и ACD показаны жирными точками, плечи сил трения – жирными отрезками. Из вышеприведенных рассуждений получаем
μ1m1gl1 =μ2m2 gl2 , |
(3) |
где l1 и l2 – плечи сил трения μ1m1g и μ2m2 g (см. рисунок). Используем теперь то обстоятельство, что центр тяжести плос-
кого треугольника расположен в точке пересечения его медиан, и что эта точка делит каждую медиану в отношении 2:1. Поэтому плечи l1 и l2 составляют 2/3 от длины перпендикуляров, опущенных из середин сторон BD и CD на границу полуплоскостей, и 1/3 от длин перпендикуляров, опущенных из вершин B и C на эту границу. А поскольку отрезки BD и CD наклонены к границе раздела полуплоскостей под одинаковыми углами, то
l1 |
= |
BD |
. |
(4) |
l |
|
|||
|
CD |
|
||
2 |
|
|
|
|
Поэтому из формул (1), (3), (4) заключаем, что отношение масс треугольников ABD и ACD равно квадратному корню из отношения коэффициентов трения:
m1 |
= |
μ1 |
. |
(5) |
|
m |
|
||||
|
μ |
2 |
|
|
|
2 |
|
|
|
|
|
Теперь используя уравнение (3) и очевидное условие m1 + m2 = m (где m – масса треугольника ABC), находим массы m1 и m2:
m1 = |
m μ2 |
|
, m2 = |
m μ1 |
|
, |
(6) |
μ + μ |
2 |
μ + μ |
2 |
||||
|
1 |
|
1 |
|
|
а затем из формулы (1) – внешнюю силу F, которую нужно приложить к вершине треугольника, чтобы равномерно перемещать треугольник по границе полуплоскостей
F = mg μ1μ2 .
г. Мирный, апрель 2009 г.
1. Так как тело движется вместе с лифтом, ускорение лифта равно ускорению тела. Найдем последнее. Для этого воспользуемся
54

вторым законом Ньютона для тела. На тело действуют сила тяжести mgG и сила со стороны пола лифта FG , направленная вертикаль-
но вверх, модуль которой равен данному в условии значению F (см. рисунок). Поэтому второй закон Ньютона для тела в проекциях на ось, направленную вертикально вверх, имеет вид
max = F −mg ,
где ax – проекция ускорения тела на рассматриваемую ось. Отсю-
да находим ускорение тела (которое равно ус- |
F |
|||||
корению лифта) |
||||||
|
|
|
||||
ax = |
F |
− g = −5 м/с2 . |
|
|
|
|
|
|
|
||||
|
|
|
|
|||
|
m |
|
|
|
||
Знак минуса для проекции ускорения на вы- |
mg |
|||||
бранную ось показывает, что вектор ускорения |
||||||
тела направлен противоположно этой оси, т.е. |
|
|
|
|||
вертикально вниз, а величина ускорения есть a =5 м/с2 .
2. Закон Клапейрона – Менделеева для начального и конечного состояний газа в рассматриваемом процессе дает
p(V + V )= νRT1; |
(1) |
|
pV = νRT2 , |
||
|
где p – давление; V – объем в конечном состоянии; ν – количество вещества газа. Деля первое уравнение (1) на второе и решая полученное уравнение, найдем
V = T2 V . T1 −T2
3. Изображение источника, находящегося на главной оптической оси линзы, лежит также на главной оптической оси. При перемещении источника по отношению к линзе перемещается и его изображение. Если при этом источник перемещается перпендикулярно главной оптической оси, его изображение будет также перемещаться перпендикулярно главной оптической оси (это следует, например, из формулы линзы, в которую не входят расстояния от источника и предмета до главной оптической оси). Этот вывод иллюстрируется рисунком, на котором источникам S и S1 отвечают
55
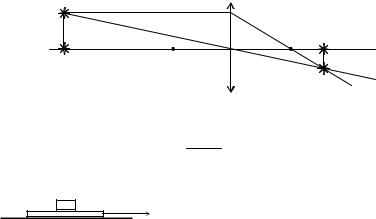
изображения S′ и S1′. Перемещение изображения a′ можно найти
|
|
|
|
|
|
|
|
|
′ |
′ |
(см. рисунок): |
|
|||||
из подобия треугольников SS1O и S S1O |
|
||||||||||||||||
|
a |
d |
|
|
|
|
|
a′ |
|
af |
|
|
|||||
|
|
= |
|
|
|
|
= |
|
, |
|
(1) |
||||||
|
a′ |
f |
|
|
d |
|
|||||||||||
где d = SO – расстояние от источника до линзы; |
′ |
– рас- |
|||||||||||||||
f = S O |
|||||||||||||||||
стояние от изображения до линзы. Далее по формуле линзы |
|
||||||||||||||||
|
|
|
|
1 |
+ |
1 |
= |
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
d |
|
|
F |
|
|
|
|
|
||||
|
|
|
|
|
|
|
f |
|
|
|
|
|
|||||
находим |
|
|
|
|
|
dF |
|
|
|
|
|
|
|
||||
|
|
|
|
f = |
|
. |
|
|
|
|
|
(2) |
|||||
|
|
|
|
d − F |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
S1 |
|
|
|
|
|
|
|
|
F |
S′ |
|
S |
|
F |
O |
|
|
|
|
|
|
S1′ |
Из формул (1) и (2) получаем |
|
|
|||
|
|
|
aF |
|
|
|
|
|
a′= d − F =1 см. |
|
|
|
m |
|
4. Сила трения, действующая между |
||
M |
F |
телом и доской, зависит от того, есть ли |
|||
|
|
|
между доской и телом проскальзыва- |
||
|
|
|
ние. |
Очевидно, при |
малых значениях |
внешней силы F доска будет двигаться с небольшим ускорением, и сила трения, действующая на тело со стороны доски, сможет заставить тело двигаться с тем же ускорением. При увеличении внешней силы сила трения между телом и доской должна возрастать и при некотором значении внешней силы достигнуть максимально возможного значения. При дальнейшем увеличении внешней силы сила трения уже не сможет увлечь тело за доской и между доской и телом возникнет проскальзывание.
56
Чтобы найти минимальную внешнюю силу, при которой возникает проскальзывание, найдем силу трения, действующую на тело при условии, что проскальзывание отсутствует. В этом случае доска и тело движутся с одинаковым ускорением, которое можно найти из второго закона Ньютона для тела и доски:
a = |
F |
. |
(1) |
|
m + M |
||||
|
|
|
Телу ускорение (1) сообщается силой трения со стороны доски. Поэтому из второго закона Ньютона для тела находим
F |
= |
mF |
. |
(2) |
|
||||
тр |
|
m + M |
|
|
Проскальзывание между телом и доской возникает, если сила трения (2) достигает максимального значения μmg :
μmg = |
mF |
F =μg(m + M ) =30 Н. |
(3) |
|
m + M |
||||
|
|
|
Поскольку данное в условии значение внешней силы F = 20 Н меньше минимальной силы, вызывающей проскальзывание (3), то тело не будет скользить относительно доски, и сила трения, действующая на него со стороны доски, определяется выражением (2)
|
F |
= |
|
mF |
=3,3 Н. |
|
|
|
|
|
|
|
|
|
|||||
|
m + M |
|
|
|
|
|
|
|
|
|
|||||||||
|
тр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5. Найдем сначала эквива- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
лентное сопротивление пред- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ставленной |
электрической |
|
|
|
|
|
V |
|
|
V |
|
|
V … |
||||||
цепи. Для этого используем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
следующий прием. Посколь- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ку данная цепь бесконечна, то |
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
|
|
||||||
выбрасывание из нее одного |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
повторяющегося звена – |
ре- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
зистора и вольтметра, взятых на рис. 1 в пунктирную рамку, – не изменяет ее сопротивление. Поэтому для эквивалентного сопротивления цепи справедливо соотношение, которое показано графически на рис. 2, на котором R – эквивалентное сопротивление цепи, r – сопротивление резистора и вольтметра. Из этого рисунка получаем уравнение для эквивалентного сопротивления
57

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R = r + |
rR |
|
, |
(1) |
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
r + R |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 −rR −r2 = 0 . |
(2) |
|||||
Решая квадратное уравнение (2), находим |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R = |
(1+ 5 )r |
|
(3) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
(второй корень уравнения является отрицательным). |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сумму |
показаний всех вольт- |
||
|
|
|
|
|
|
|
|
|
r |
|
|
метров можно найти из следующих |
|||||||||
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соображений. Поскольку сопротив- |
||||
|
|
|
|
= |
|
|
|
|
|
r |
|
|
|
|
R |
ление каждого вольтметра r, то ес- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ли вольтметр показывает напряже- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ние Ui , |
для тока через него Ii |
|||||
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
справедливо соотношение |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ui = rIi . |
|
(4) |
|||
Поэтому для суммы показаний всех вольтметров имеем |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑Ui = r∑Ii . |
(5) |
||||
ii
Апоскольку при параллельном соединении элементов токи складываются, то сумма токов, текущих через все вольтметры, равна току, втекающему в электрическую цепь, т.е.
∑Ii = |
U |
= |
2U |
|
|
. |
(6) |
|
( |
) |
|
||||
|
R |
r |
|
||||
i |
1+ 5 |
|
|
||||
|
|
|
|
||||
Отсюда и из формулы (5) окончательно получаем
∑Ui = |
|
2U |
|
|
. |
|
( |
+ |
5 |
) |
|||
i |
|
|||||
1 |
|
|
г. Новгород, апрель 2009 г.
1.См. решение задачи 1 из заключительного тура, г. Мирный.
2.См. решение задачи 2 из заключительного тура, г. Мирный.
58
3. Поскольку через сопротивления R1, R2 и R3 течет одинаковый ток, из закона Джоуля – Ленца
P = I 2 R
следует, что среди этих сопротивлений наибольшая тепловая мощность будет выделяться на сопротивлении R3. Аналогично среди сопротивлений R4, R5 и R6 наибольшая мощность будет выделяться на сопротивлении R6.
Сравним мощности тока на сопротивлениях R3 и R6. По закону Ома для участка цепи найдем силу тока в верхнем и нижнем участке цепи
Iв = |
|
U |
|
, |
Iн = |
|
U |
|
, |
R + R + R |
R + R + R |
||||||||
|
1 |
2 |
3 |
|
|
4 |
5 |
6 |
|
где U – напряжение, приложенное к цепи, а затем по закону Джоуля – Ленца – мощности, выделяемые на сопротивлениях R3 и R6:
|
|
|
U 2 R |
|
|
|
|
|
|
3U 2 |
|
||
P3 = |
|
3 |
|
|
|
|
= |
|
|
[Вт] , |
|
||
(R + R + R )2 |
|
36 |
|
|
|||||||||
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
||
|
|
|
U 2 R |
|
|
|
|
|
6U 2 |
|
|||
P6 = |
|
|
6 |
|
|
|
= |
|
|
[Вт] . |
(1) |
||
(R + R + R |
)2 |
|
225 |
||||||||||
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
||
Поскольку P3 > P6 (приблизительно в три раза), из формулы (1)
заключаем, что наибольшая мощность в приведенной схеме будет выделяться на сопротивлении R3. При U =100 В вычисления по первой из формул (1) дают
P3 =833 Вт.
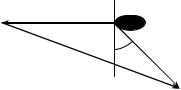
4. Треугольник сложения скоростей, отвечающий рассматриваемой в задаче ситуацииG , изображен на рисунке. Здесь υ – вектор скорости корабля относительно земли (направленный по условию «на запад»); υG1 – вектор скорости ветра относи-
υ
α υ1
u
тельно земли, который по условию направлен на юго-восток под углом α к меридиану (пунктирный отрезок, перпендикулярный
59
