§3. Взаимное положение прямых на плоскости.

Угол между прямыми (наименьший из двух смежных углов, полученных при пересечении прямых)

φ

Прямые заданы общим уравнением	Прямые заданы уравнением с угловым коэффициентом
А1х+В1у+С1=0 А2х+В2у+С2=0	у=к1x+b1 y=k2x+b2
	tg𝛗=

Условие параллельности двух прямых.

Прямые заданы общим уравнением	Прямые заданы уравнением с угловым коэффициентом
А1х+В1у+С1=0 А2х+В2у+С2=0	у=к1x+b1 y=k2x+b2
(1)(2)	(1)(2)

Условие перпендикулярности двух прямых.

Прямые заданы общим уравнением	Прямые заданы уравнением с угловым коэффициентом
А1х+В1у+С1=0 А2х+В2у+С2=0	у=к1x+b1 y=k2x+b2
(1)(2)	(1)(2)

Нормальное уравнение прямой.

x;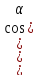+(²=1; p>0 (параметр «р» определяет расстояние прямой от точки начала координат)

Примечание:

Если известно общее уравнение прямой, то нормальное уравнение можно получить по следующему правилу:

Ах+Ву+С=0; находим нормирующий множитель 𝛍=-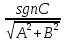, гдеозначает знак числа «С» в заданной формуле, тогда

𝛍*B; p=-𝛍*C.

Пример.

Найти нормальное уравнение прямой и расстояние прямой до начала координат.

(L): 3x-4y+10=0.

𝛍=-=-=-

-

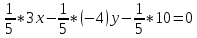
-0,6x+0.8y-2=0

расстояние до начала координат

2.Расстояние от точки М₀(х₀;у₀) до прямой (L) Ax+By+C=0.

𝛒(M₀;L)=

3.Расстояние между параллельными прямыми.

Обозначим расстояние между параллельными прямыми d

y

d

ρ₁

ρ₂

x

L₁

L₂

d=𝛒₁+𝛒₂ если прямые лежат по разные стороны от начала координат, то нужно сложить расстояния для каждой прямой от точки начала координат.

y

L₂

ρ₂

L₁

ρ₁

x

d

d=𝛒₂-𝛒₁ если прямые лежат по одну сторону от начала координат, то нужно найти модуль разности расстояний этих прямых до начала координат.

Для нахождения расстояния между параллельными прямыми можно придерживаться следующей последовательности действий.

1.Так как прямые параллельны, приведите уравнения прямых к виду так, чтобы коэффициенты у переменных были равны:

(L₁): Ax+Вy+C₁=0; (L₂): Ax+By+C₂=0; C₁≠C₂

2. Обратите внимание на знаки свободных членов, а именно: если знаки разные (С₁*С₂0), то прямые лежат по разные стороны от начала координат, а , если одного знака (С₁*С₂>0), то по одну сторону от начала координат.

3.Для нахождения расстояния между параллельными прямыми можете использовать следующие формулы:

. d=; (С₁*С₂0); d=; (С₁*С₂>0),

Пример 1:

Найти расстояние между прямыми (L₁):4х-10у+9=0; (L₂): 2x-5y-6=0.

Решение:

={4;-10}; ={2;-5} прямые параллельны.

(L₁):4х-10у+9=0 2х-5у+4.5=0С₁=4,5;С₂=-6. d=;(С₁*С₂0)d=

Пример 2.

Найти расстояние между прямыми (L₁):3х-2у-5=0; (L₂): 12x-8y-6=0

Решение:

={3;-2}; ={12;-8} прямые параллельны.

(L₂): 12x-8y-6=03х-2у-1,5=0  d=; (С₁*С₂>0)d=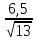

§4.Взаимное положение двух плоскостей.

Определение:

Углом между плоскостями называют наименьший из двух смежных двугранных углов.

Напомним, что двугранный угол измеряется линейным углом.

Нам удобнее измерять двугранный угол углом между нормалями данных плоскостей, который равен соответствующему линейному (углы с соответственно перпендикулярными сторонами)

P₂

n₁

φ

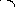
φ

n₂

P₁

(P₁): A₁x+B₁y+C₁z+D₁=0; ={A₁;B₁;C₁}

(P₂) ): A₂x+y+C₂z+D₂=0; ={A₂;B₂;C₂}

=  (угол должен быть острым, поэтому значение косинуса берём по модулю)

Условия параллельности двух плоскостей.

(P₁)(P₂) 

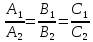
Условия перпендикулярности двух плоскостей.

(P₁)(P₂) A₁*A₂+B₁*B₂+C₁*C₂=0

Нормальное уравнение плоскости.

x;+(²+=1;p>0 (параметр «р» определяет расстояние плоскости от точки начала координат)

Примечание:

Если известно общее уравнение плоскости, то нормальное уравнение можно получить по следующему правилу:

Ах+Ву+Сz+D=0; находим нормирующий множитель 𝛍=-, гдеозначает знак числа «D» в заданной формуле, тогда

𝛍*B; =𝛍*C; p=-𝛍D

Пример.

Найти нормальное уравнение плоскости и расстояние плоскости до начала координат.

(L): 3x-4y+10z-8=0.

𝛍=-=-=



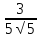х-у+z-0 p=

расстояние до начала координат

2.Расстояние от точки М₀(х₀;у₀;z₀) до плоскости (P) Ax+By+Cz+D=0.

𝛒(M₀;P)=

3.Расстояние между параллельными плоскостями.

Обозначим расстояние между параллельными плоскостями d

По аналогии с формулами, полученными для расстояния между параллельными прямыми , получим аналогичные формулы для определения расстояния между параллельными плоскостями.

1.Так как плоскости параллельны, приведите уравнения плоскостей к виду так, чтобы коэффициенты у переменных были равны:

(L₁): Ax+Dy+Cz+D₁=0; (L₂): Ax+By+Cz+D₂=0; D₁≠D₂

2. Обратите внимание на знаки свободных членов, а именно: если знаки разные (D₁*D₂0), то плоскости лежат по разные стороны от начала координат, а , если одного знака (D₁*D₂>0), то по одну сторону от начала координат.

3.Для нахождения расстояния между параллельными плоскостями можете использовать следующие формулы:

. d=; (D₁*D₂0); d=; (D₁*D₂>0),

Пример 1.

Найти расстояние между плоскостями:

(P₁): 3x-2y+5z-8=0; (P₂): -12x+8y-20z+7=0

Решение:

(P₁): 3x-2y+5z-8=0 ; ={3;-2;5};

(P₂): -12x+8y-20z+7=0; ={-12;8;-20}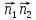

(P₂): -12x+8y-20z+7=03x-2y+5z-7/4=0

D₁=-8; D₂=-7/4 D₁*D₂>0 d==

Пример 2.

Найти расстояние между плоскостями:

(P₁): 6x-2y+10z+15=0; (P₂): 3x-y+2z-4=0

Решение:

(P₁): 6x-2y+10z+15=0; {6;-2;10}; (P₂): 3x-y+5z-4=0; ={3;-1;5}

(P₁): 6x-2y+10z+15=03x-y+5z+7,5=0D₁=7,5; D₂=-4

D₁*D₂0); d==

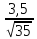
Пример 3.

Найти расстояние от точки М₀(0;-1;2) до плоскости (P), проходящей через три точки М₁(0;2;-4); М₂(-1;5;2); М₃(1;3;2).

Решение.

M₀

M₂

(Р)

M₁

M₃

Найдём координаты направляющих векторов данной плоскости (Р)

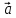=={-1;3;6}; =={1;1;6}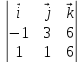===12+12-4

={12;12;-4} {3;3;-1}уравнение плоскости ищем в виде:

A(x-x₁)+B(y-y₁)+C(z-z₁)=03(x-0)+3(y-2)-(z+4)=03x+3y-z-10=0 (P)

Расстояние от точки М₀(0;-1;2) до плоскости (Р) находим по формуле:

𝛒(M₀;P)===

Лекция 2.

Прямая в пространстве. Взаимное положение прямой и плоскости в пространстве.

§1Различные уравнения прямой в пространстве.

П⁰1. Общее уравнение прямой в пространстве.

Р₂

Р₁

L

Если плоскости не параллельны , то прямую можно задать пересечением двух плоскостей, т. е. системой уравнений: ;

={A₁;B₁;C₁}нормаль плоскости (Р₁);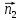={A₂;B₂;C₂}нормаль плоскости (Р₂) (L)=(P₁)∩(P₂)

П⁰2. Каноническое уравнение прямой.

Задача.

Дано: М₀(x₀;y₀;z₀); ={l;m;k}

Найти уравнение прямой (L): M₀(L);  (L)

Решение:

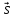
L

M₀

M(x;y;z)

Возьмём произвольную точку M(x;y;z)(L)={x-x₀;y-y₀;z-z₀}

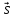
По условию  (L)  каноническое уравнение прямой (уравнение прямой через точку с направляющем вектором)

П⁰3. Параметрическое уравнение прямой.

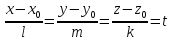
tR

(параметрическое уравнение прямой в пространстве)

П⁰4Уравнение прямой через две точки.

(L)

M₂

M₁

Используем каноническое уравнение прямой:

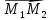=={x₂-x₁;y₂-y₁;z₂-z₁}  уравнение прямой через две точки.

П⁰5.Связь между общим и каноническим уравнениями прямой в пространстве.

Задача.

Пусть прямая (L) задана общим уравнением:

Найти каноническое уравнение прямой:

Решение

Т.к. прямая получается при пересечении двух плоскостей, то

(L) ; (L);  =={l;m;k}

Чтобы найти точку, через которую проходит прямая, достаточно найти частное решение данной системы M₀(x₀;y₀;z₀)

Пример

Дано :прямая (L) задана общим уравнением:

(L)

Найти каноническое уравнение прямой.

Решение:

={2;-3;4}; ={5;1;-3}==5+26+17

={5;26;17}

Т.к.система имеет бесконечное множество решений (ранги матриц расширенной и системы равны r(A)=r(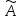)=2; число неизвестных равно трём), то имеем две базисных и одну свободную переменные. Пусть свободной переменной будет переменнаяz. Для нахождения частного решения зададим числовое значение, например, z=0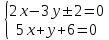

3

17x+16=0 x=-

M₀(;;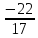0)(L):

Примечание: Очевидно, что это не единственное уравнение прямой, т.к. частных решений бесконечно много и коллинеарных направляющих векторов тоже бесконечно много.