
- •НИУ ВШЭ – Пермь
- •Определение формального языка
- •Определение формального языка:
- •Этапы компиляции
- •Понятие вывода и определение языка, порождаемого грамматикой
- •Понятие вывода и определение языка, порождаемого грамматикой
- •Понятие вывода и определение языка, порождаемого грамматикой
- •Понятие вывода и определение языка, порождаемого грамматикой
- •Пример вывода в грамматике целых чисел
- •Пример вывода в грамматике целых чисел
- •Определение языка, порождаемого грамматикой
- •Определение языка, порождаемого грамматикой: примеры
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений

Определение языка, порождаемого грамматикой
Цепочки σ, выводимые из начального символа S грамматики G S =>* σ
называются сентенциальными формами грамматики.
Если сентенциальная форма состоит только из терминальных символов, то она называется сентенцией.
Множество всех сентенций грамматики G образует язык, порождаемый грамматикой G, и обозначается L(G).
Две различные грамматики G1 и G2, т.е. грамматики с различным
набором правил и различными множествами нетерминальных символов могут порождать один и тот же язык: L(G1) = L(G2).
Грамматики, порождающие один и тот же язык, называются
11 эквивалентными.

Определение языка, порождаемого грамматикой: примеры
Например, грамматики
G1 = {A, N1, P1, S1} и G2 = {A, N2, P2, S2},
где
A = {0, 1},
N1 = {S1, F, B}, P1 = {S1 ::= FB | F1S1, F ::= 01, B ::= 1},
N2 = {S2, C, D}, P2 = {S2 ::= 01C, C ::= D1, D ::= | 101D}
порождают разными способами одно и то же множество сентенций вида
011n,
т.е. строк, состоящих из повторяющихся (сколько угодно раз) 12 комбинаций 011 (например: 011, 011011, 011011011 и т.д.).

Пример: грамматика выражений
Рассмотрим грамматику алгебраических выражений, порождающую строки, соответствующие правилам записи арифметических выражений.
Любое выражение может быть записано в виде строки символов в алфавите
{a, b, c, .., z, 0, 1, .., 9, + , –, *, /, (, )}.
Знак аддитивной операции – это знаки операций типа сложения (+ или –). Знак мультипликативной операции – это операции типа
умножения (* или / ). Какие-либо другие операции, в том числе унарный минус и унарный плюс не используются.
Для простоты будем предполагать, что переменная задается
одной буквой, а число – одной или несколькими цифрами (т.е.
13 является целым без знака).

Пример: грамматика выражений
Грамматика выражений включает следующие правила (нетерминальные символы выделены угловыми скобками):
<Expression> ::= <Addend >{ +<Addend> | – <Addend> } <Addend> ::= <Factor> { *<Factor> | /<Factor> } <Factor> ::= <Letter> | <Number> | ( <Expression >)
<Letter > ::= a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z
<Number> ::= <Digit > {<Digit >}
<Digit > ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
14

Пример: грамматика выражений
Примеры выражений, записанных на основе этих правил: a+b
(c–d) (c–d)*(c+d) m*n+4 s–(75/k+r)/a 1 0011999
f
(((1)))
15 0–9

Пример: грамматика выражений
Эти правила определяют Выражение через Слагаемое,
Слагаемое через Множитель, Множитель через Переменную,
Число и Выражение, таким образом, Выражение определяется
|
(транзитивно) через Выражение. |
|
Альтернативное определение Множителя как Переменной или |
|
Числа – выход из рекурсии. Эти понятия здесь являются |
|
первичными. |
|
Ситуация подобна рекурсивным процедурам. |
|
Имеется косвенная рекурсия в определении понятия Выражения |
|
(равно как и понятий Слагаемого и Множителя) и альтернативная |
|
нерекурсивная ветвь, позволяющая остановиться и сформировать |
|
алгебраическое выражение конечной длины. |
16 |
Каждому правилу можно поставить в соответствие процедуру |
синтаксического разбора. |
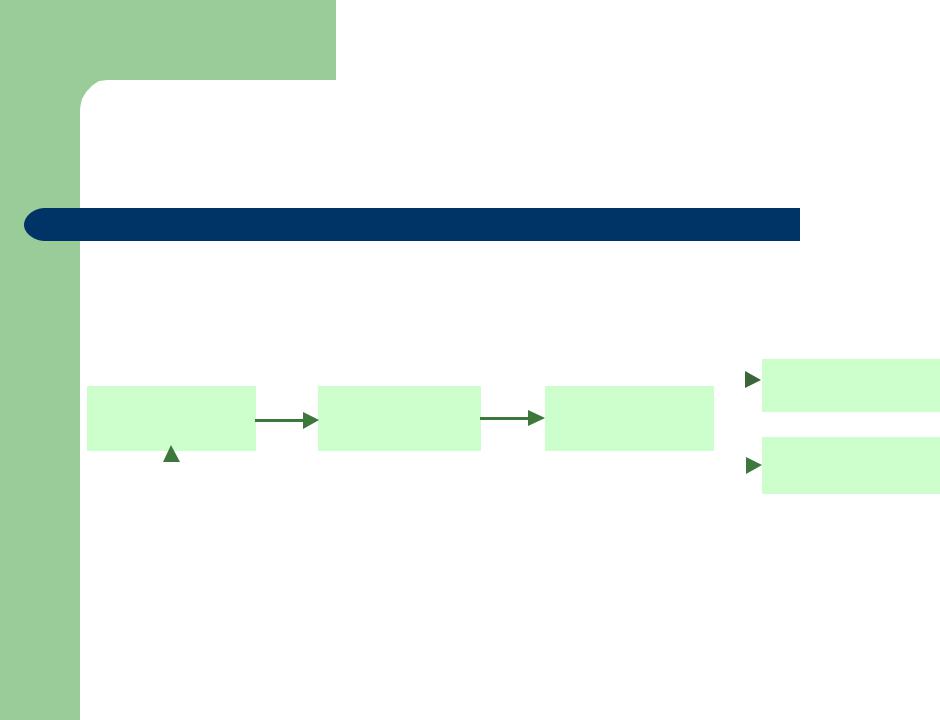
Пример: грамматика выражений
|
|
|
|
|
|
|
|
|
|
Число |
|
|
|
|
|
|
|
|
|
|
|
Выражение |
|
Слагаемое |
Множитель |
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Переменная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17
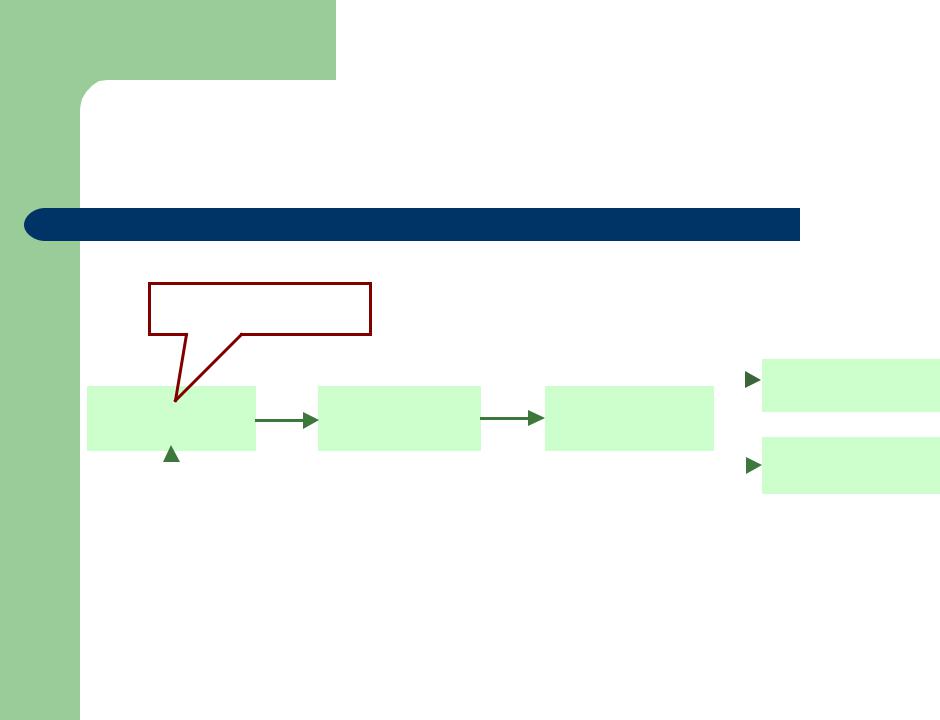
Пример: грамматика выражений
(c–d)*(1+d)
|
|
|
|
|
|
|
|
|
|
Число |
|
|
|
|
|
|
|
|
|
|
|
Выражение |
|
Слагаемое |
Множитель |
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Переменная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18
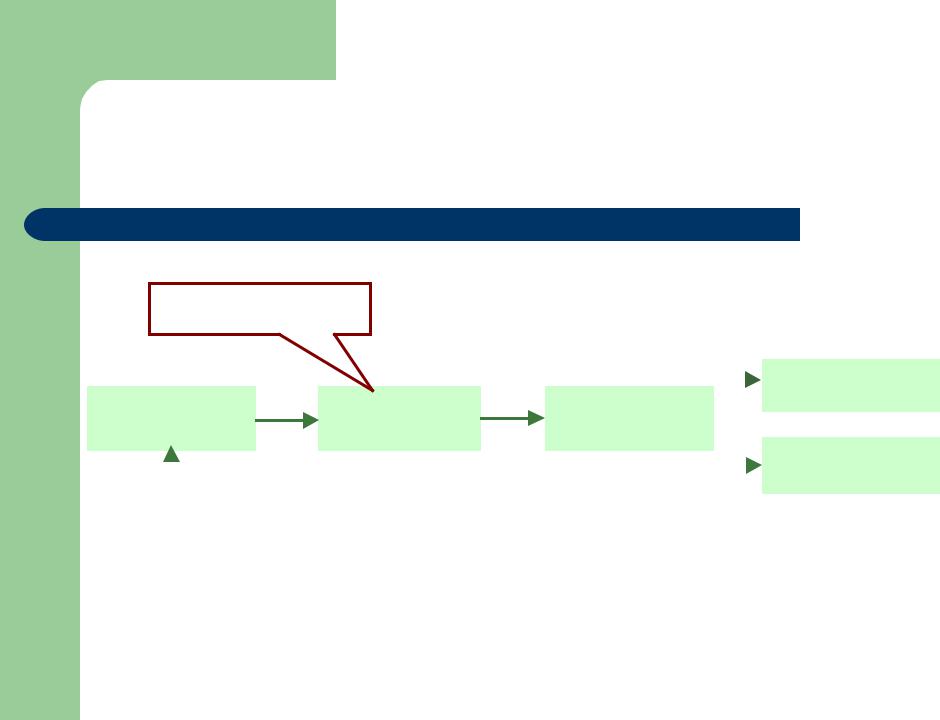
Пример: грамматика выражений
(c–d)*(1+d)
|
|
|
|
|
|
|
|
|
|
Число |
|
|
|
|
|
|
|
|
|
|
|
Выражение |
|
Слагаемое |
Множитель |
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Переменная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19
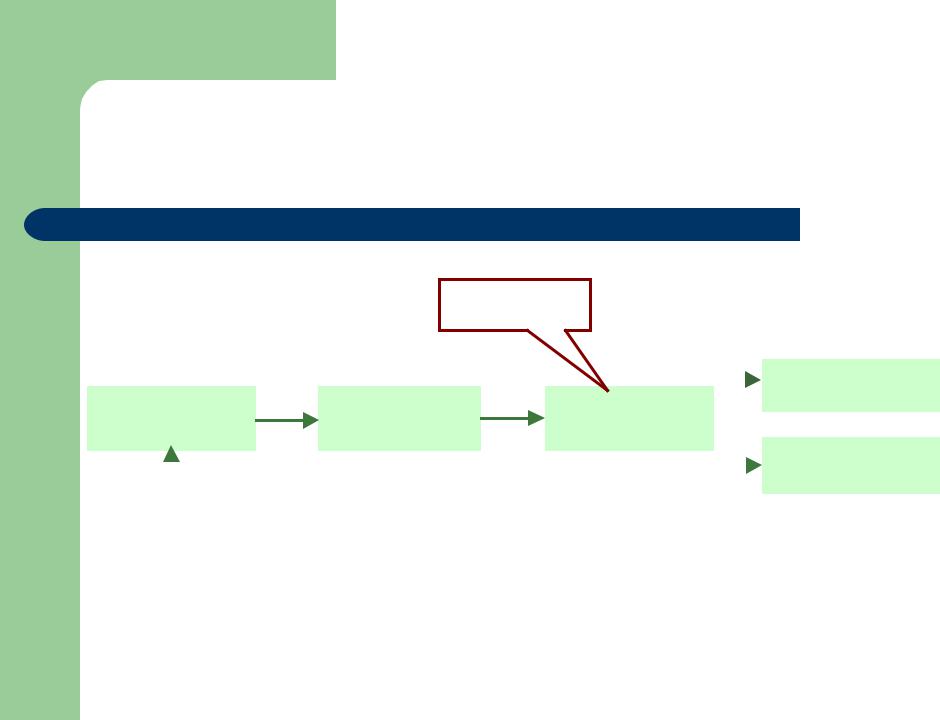
Пример: грамматика выражений
(c–d)
|
|
|
|
|
|
|
|
|
|
Число |
|
|
|
|
|
|
|
|
|
|
|
Выражение |
|
Слагаемое |
Множитель |
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Переменная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20
