
- •НИУ ВШЭ – Пермь
- •Определение формального языка
- •Определение формального языка:
- •Этапы компиляции
- •Понятие вывода и определение языка, порождаемого грамматикой
- •Понятие вывода и определение языка, порождаемого грамматикой
- •Понятие вывода и определение языка, порождаемого грамматикой
- •Понятие вывода и определение языка, порождаемого грамматикой
- •Пример вывода в грамматике целых чисел
- •Пример вывода в грамматике целых чисел
- •Определение языка, порождаемого грамматикой
- •Определение языка, порождаемого грамматикой: примеры
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений
- •Пример: грамматика выражений

НИУ ВШЭ – Пермь
Факультет бизнес-информатики
Кафедра информационных технологий в бизнесе
Формальные языки и основы трансляции
Материалы курса «Теоретические основы информатики»
Лекция 7
Лядова Л.Н.
Пермь 2012

Определение формального языка
Введем конечное множество символов
A = {a1 , a2 ,..., an}, которое назовем алфавитом языка.
Из символов алфавита можно составлять всевозможные цепочки различной длины, записывая символы друг за другом.
Минимальная цепочка имеет длину 0, не содержит ни одного символа, называется пустой цепочкой и обозначается (греческая лямбда). Ограничения сверху на длину цепочек нет.
Любой символ алфавита может входить в цепочку произвольное число раз.
Бесконечное множество всех возможных цепочек обозначается
2A*.Любое подмножество L A* называется языком.

Определение формального языка:
понятие грамматики
Грамматика представляет набор из четырех элементов: G = {A, N, P, S},
где A – алфавит или множество терминальных символов, N – множество нетерминальных символов,
P – множество правил грамматики,
S N – начальный (целевой) символ грамматики.
Начальный символ S грамматики представляет собой основное (базовое) понятие, базовая конструкция языка.
Правила (в литературе также встречается термин продукции) P грамматики задают отношения между различными нетерминальными и терминальными символами, описывают
3правильные с точки зрения языка конструкции.

Этапы компиляции
|
Исходная программа |
|
|
|
|
|
Модуль ввода-вывода |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последовательность |
|
||
|
|
|
литер |
|
|
|
|
Лексический анализатор |
|
|
|
|
|
|
|
|
|
|
|
|
Последовательность |
|
||
|
|
символов |
|
|
|
|
|
Синтаксический анализатор |
|
|
|
|
|
|
|
|
|
|
|
|
Программа во внутреннем |
|
||
|
представлении |
|
||
|
|
|
Семантический анализатор |
|
|
|
|
|
|
|
|
|
|
|
|
Программа во внутреннем |
|
||
4 |
представлении |
|
||
|
|
Генератор кода |
|
|
|
|
|
||
|
|
|
|
|
Листинг
Лексические
ошибки
Синтаксические
ошибки
Семантические
ошибки
Объектный код

Понятие вывода и определение языка, порождаемого грамматикой
Грамматики в сжатой форме задают языки – множества цепочек из A*. Грамматику и язык связывает понятие вывода.
Пусть σ – некоторая цепочка, состоящая из терминальных и нетерминальных символов, включающая, в частности, подцепочку β:
σ = 1β 2.
Здесь 1 и 2 – подцепочки, а β – левая часть одного из правил грамматики (β ::= ).
Правая часть состоит из нескольких альтернатив:= π1 | π2 | … | πk ,
где πi – цепочки. Тогда из цепочки σ = 1β 2 можно получить с
5 |
помощью подстановок (замены β на πi) новые цепочки символов: |
||||||||
σ’ = |
π |
, σ’’ = |
|
1 |
π , ... , σ(k) = |
|
π |
. |
|
|
|
1 1 2 |
|
|
2 2 |
|
1 k 2 |
|
|

Понятие вывода и определение языка, порождаемого грамматикой
Говорят, что цепочки σ(i) выводятся из цепочки σ за один шаг вывода (непосредственно выводятся) с помощью правила
грамматики. Обычно на каждом шаге вывода берется только одна из альтернатив и, соответственно, получается только одна новая цепочка. Обозначим ее σ1.
К вновь образованной цепочке можно (если она не состоит сплошь из терминальных символов) применить какое-нибудь правило грамматики и сделать еще один шаг вывода, получив цепочку σ2 и так далее:
σ => σ1 => σ2 => σ3 => … => σn.
Записанная последовательность называется выводом в данной формальной грамматике, а любая из цепочек σi называется
6выводимой из цепочки σ, причем σi+1 называется непосредственно
выводимой из σ: σ => σ + 1.

Понятие вывода и определение языка, порождаемого грамматикой
Отношение выводимости (не обязательно непосредственной) обозначают =>*. Таким образом, можно записать:
σ =>* σn.
Отношению выводимости можно придать свойство рефлексивности, т.е. считать, что, может быть, никакое правило
вообще не применялось. В таких случаях цепочка σ остается неизменной: σn = σ.
Вывод законченный, если для полученной цепочки нельзя больше сделать ни одного шага вывода, т.е. полученная цепочка содержит только терминальные символы.
Вывод называется левосторонним, если на каждом шаге вывода правило применяется к самому левому нетерминальному символу,
7правосторонним – если к самому правому.

Понятие вывода и определение языка, порождаемого грамматикой
Дерево вывода – это дерево, которое соответствует цепочке вывода и удовлетворяет условиям:
1.Каждая вершина – это символ грамматики из V = A N.
2.Корень – это вершина, соответствующая начальному (целевому) символу.
3.Листья – символы из A – терминальные символы (или пустой символ ).
4.Если узел помечен символом B N, а связанные с ним узлы (дочерние) – символами b1, b2, …, bn, n > 0 и для любого 0 < i ≤ n:
|
bn A N { }, |
|
то в грамматике G есть правило |
8 |
B ::= b1 b2 … bn R. |
|

Пример вывода в грамматике целых чисел
(1) – построение цепочки выводов
Множество нетерминальных символов: N = {S, T, F},
(здесь для сокращения записи введены следующие обозначения нетерминальных символов: S – целое число со знаком, T – целое число без знака, F – цифра).
Множество продукций:
P = {S::=T|+T|–T, T::=F|FT,
F::=0|1|2|3|4|5|6|7|8|9},
Рассмотрим вывод для строки – проверим, выводимо ли число –479. Построим цепочку выводов:
S –T –FT –FFT –FFF –4FF –47F –479
Вывод законченный – больше нельзя выполнить замены, получена
9строка, состоящая только из терминальных символов.
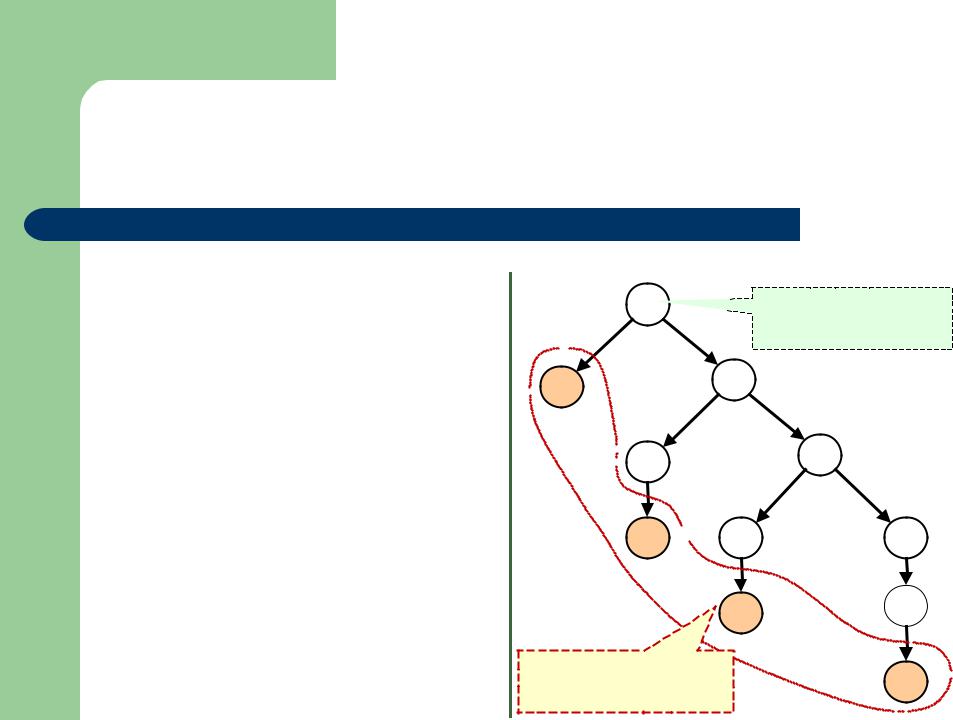
Пример вывода в грамматике целых чисел
(1) – построение дерева выводов
Построим дерево вывода для числа –479.
|
Алфавит |
|
A = {0,1, 2, 3, 4, 5, 6, 7, 8, 9, +, –} |
|
Множество нетерминальных |
|
символов |
|
N = {S, T, F}, |
|
множество продукций: |
|
P = {S::=T|+T|–T, |
|
T::=F|FT, |
|
F::=0|1|2|3|4|5|6|7|8|9}, |
|
где |
|
S – целое число со знаком, |
10 |
T – целое число без знака, |
F – цифра |
S










– |
T |
|
F
4 
 F
F
7
Листья дерева вывода –479
Корень дерева вывода
T
T
F
9
