вышмат / теория / 5-9. Агебраические уравнения. Комплексная плоскость. Извлечение корня. Уравнения прямой

5. Алгебраические уравнения и комплексные числа.

Комплексные числа – расширение действительных чисел с помощью такого числа i, которое в квадрате даёт -1. Такие числа имеют вид a+ib. A – реальная часть(Re Z), b – мнимая часть(Im Z).

Два комплексных числа называют равными в том случае, если Re Z₁ = Re Z₂ , а Im Z₁ = Im Z₂ . Для комплексных чисел выполняются все алгебраические свойства.

Свойства сложения:

1. Z₁ + (Z₂ + Z₃) = (Z₁ + Z₂) + Z₃ Ассоциативность сложения

2. Z₁ + Z₂ = Z₂ + Z₁ Коммутативность сложения

3. Z + (0 + i0) = Z Существование нуля

4. Для Z = X + iY существует –Z, в котором Re Z = -X, a Im Z = -Y Существование противоположности

По определению, произведением двух комплексных чисел Z = X +iY и Z = X + iY будет такая вещь:

Z₁ х Z₂ = (X₁X₂ – Y₁Y₂) + i(X₁ Y₂ + X₂Y₁)

Свойства умножения:

1. Z₁(Z₂Z₃) = (Z₁Z₂)Z₃ Ассоциативность умножения

2. Z₁Z₂ = Z₂Z₁ Коммутативность умножения

3. Z(1 + i0) Умножение на единицу

4. Z x Z^-1 = 1 Обратное число

Дистрибутивность:

1. Z(W₁ + W₂) = ZW₁ + ZW₂

При участии в операциях эти числе ведут себя как обыкновенные полиномы(многочлены).

Алгебраическое уравнение – это когда над числами совершаются операции сложения, вычитания, умножения, деления, извлечение корня и возведение в степень, и при этом это всё чему-то равно. (операции связанные с тригонометрией или логарифмами именуются транцендентными)

Квадрат комплексного числа может быть как отрицательным и комплексным(так у Жолкова).

Множество комплексных чисел обозначается С(сильно так нарисованная)

При отождествлении комплексного числа X + i0 с целым числом X, мы получаем изоморфность, то есть множество С полностью включает в себя множество R.

Комплексно-сопряженное число() это комплексное число с равной по модулю, но противоположной по знаку мнимой частью. Если комплексное число равно своему сопряженному, то это действительное число.

|Z| =

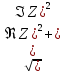
Z = |Z²|

Деление комплексных чисел – крайне сложная вещь. Поэтому лучше используя приведённые выше формулы заменять деление умножением:= =

6. Комплексная плоскость.

Образом числа 1+i0 является точка с координатами (1;0), а 0+i1, соответственно, (0;1). Для действительных чисел это будет стандартным изоморфическим отождествлением. Ось же OY будет отождествлением для мнимых чисел. Полное сопряженное число – это точка на плоскости. Поэтому числовая плоскость называется комплексной.

Комплексно-сопряженное число – отражение точки относительно оси OX.

Тригонометрическая форма комплексного числа:

Z = , где 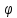- угол наклона вектора(от нуля до соответствующей точки).

= = ; = = ; = =

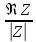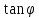Геометрическая интерпретация алгебраических операций:

Сложение – сдвиг на вектор-слагаемое;

Умножение – поворот на угол(равный аргументу(углу)множителя)с растяжением;

Возведение в степень:

7. Извлечение корня из комплексного числа.

Тригонометрический вид

Нетригонометрический вид

Для Y ≥ 0

W =

Для Y < 0

W =

Основная теорема алгебры заключается в том, что у любого ненулевого и неконстантного многочлена есть хотя бы один комплексный корень.

Единственность множества комплексных чисел подтверждается тем, что если на пространстве R² введена какая-либо операция умножения, превращающая его в поле, то получившееся поле будет алгебраически изоморфно С.(так у Жолкова написано. Я сам не совсем понимаю, что это значит.)

Формула Фробениуса заключается в том, что ни в каком n-мерном пространстве Rⁿ нельзя ввести операцию умножения, превращающую его в поле.

8. Уравнения прямой(параметрическое, каноническое, общее).

Параметрическое уравнение прямой.

Пусть конец некоего вектора (точка P₀)лежит на прямой, параллельной данному ненулевому вектору(). Тогда произвольная точка P на этой же прямой будет концом вектора . Вектор 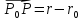полностью лежит на этой прямой, следовательно, он коллинеарен данному ненулевому вектору. Существует такое число t, что .

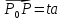r = r₀ + ta – параметрическое уравнение прямой.

Если записывать все эти вещи в координатах, то получится следующее:

X = X₀ + ta_x ,

Y = Y₀ + ta_{y .}

Если данный ненулевой вектор не параллелен ни одной из координатных осей, то координатные уравнения равносильны уравнению , которое называют каноническим.

Из канонического уравнения прямой мы получаем: –a_yx + a_xy + (x₀a_y – y₀a_x) = 0

Обозначив –a_y через А, a_x через В а (x₀a_y – y₀a_x) через С, получаем Ax + By + C = 0. Это уравнение называется общим уравнением прямой на плоскости.

9. Уравнения прямой(с угл.коэфф., в отрезках, через 2 тчк.)

Разделив общее уравнение прямой на коэф. В, мы получаем уравнение вида y = kx + b, где k = -A/B, a b = -C/B. Такое уравнение называется уравнением прямой с угловым коэффициентом.

В этом уравннеии k = tg

Уравнение прямой в отрезках

Прямая, проходящая через точки А = (а,0) и В = (0, b) имеет координатное уравнение . Заданная такой формулой, прямая отсекает отрезки ОА и ОВ на осях координат, потому она и называется уравнением в отрезках.

Уравнение через 2 точки.

Для определения прямой, проходящей через точки Р₁ = (х₁,у₁) и Р₂ = (х₂,у₂) , заметим, что вектор Р₁Р₂ лежит на этой прямой. Длиной вектора будет соответственно (х₂ – х₁,у₂ – у₁). Каноническое уравнение этой прямой будет выглядеть так: . Это и есть уравнение прямой через 2 точки.