
Макро Арефьев с хсехелп / Вариант 1
.doc|
|
ТЕОРИЯ РОСТА
Контрольная работа
ФИО _______________________________________ Группа ____________ |
Теоретическое задание.
Фундаментальные вопросы теории роста и модель Солоу.
Задача
Рассмотрим модель Солоу с производственной функцией Кобба-Дугласа и с природными ресурсами. Предпосылки модели задаются следующей системой уравнений:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
где
![]() - выпуск,
- выпуск,
![]() - капитал,
- капитал,
![]() - эффективность труда,
- эффективность труда,
![]() - труд,
- труд,
![]() - природные ресурсы,
- природные ресурсы,
![]() - эластичность выпуска по капиталу,
- эластичность выпуска по капиталу,
![]() - темп технического прогресса,
- темп технического прогресса,
![]() - темп роста населения,
- темп роста населения,
![]() - темп выбытия природных ресурсов,
- темп выбытия природных ресурсов,
![]() - норма сбережения,
- норма сбережения,
![]() - норма износа оборудования.
- норма износа оборудования.
Пусть
![]() - капиталоемкость продукции,
- капиталоемкость продукции,
![]() .
.
Задания.
-
Из гипотез модели выразите линейное дифференциальное уравнение относительно капиталоемкости продукции. Решите это уравнение.
-
Используя решение, полученное в предыдущем пункте задачи, определите, к чему стремится капиталоемкость продукции на траектории сбалансированного роста через параметры модели.
-
Выразите выпуск на траектории сбалансированного роста через капиталоемкость продукции на траектории сбалансированного роста. Из полученного выражения определите темпы роста экономики на траектории сбалансированного роста.
-
Выразите потребление на момент
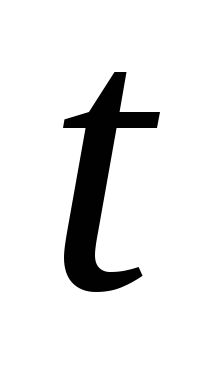 через капиталоемкость продукции на
момент
через капиталоемкость продукции на
момент
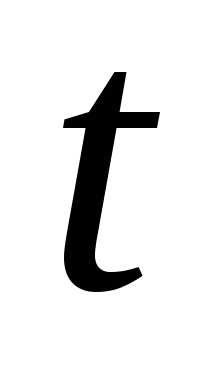 ,
эффективный труд на момент
,
эффективный труд на момент
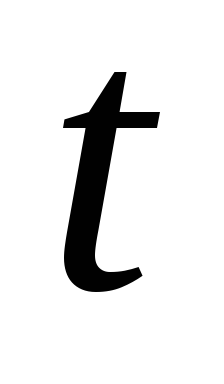 и параметры модели. Используя выражение
для капиталоемкости продукции на
траектории сбалансированного роста,
определите норму сбережения,
соответствующую золотому правилу. Как
норма сбережений, соответствующая
золотому правилу в модели Солоу с
природными ресурсами соотносится с
нормой сбережений, соответствующей
золотому правилу в модели Солоу без
природных ресурсов?
и параметры модели. Используя выражение
для капиталоемкости продукции на
траектории сбалансированного роста,
определите норму сбережения,
соответствующую золотому правилу. Как
норма сбережений, соответствующая
золотому правилу в модели Солоу с
природными ресурсами соотносится с
нормой сбережений, соответствующей
золотому правилу в модели Солоу без
природных ресурсов? -
Из условий максимизации прибыли фирмой, выразите ставку процента через капитал, природные ресурсы, эффективный труд и параметры модели. Затем подставьте
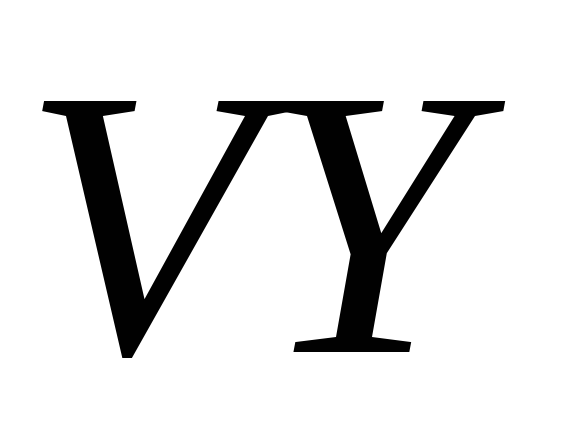 вместо
вместо
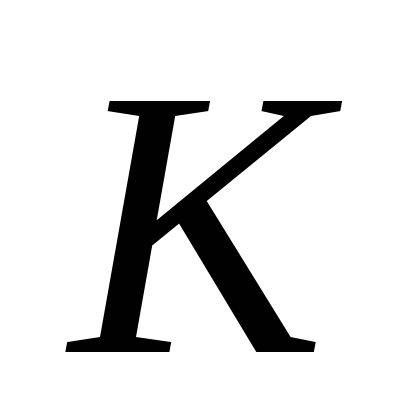 ,
,
 из пункта 3, и выразите ставку процента
через капиталоемкость продукции,
природные ресурсы, эффективный труд и
параметры модели. После этого, используя
результат задания 2, выразите ставку
процента на траектории сбалансированного
роста через параметры модели.
из пункта 3, и выразите ставку процента
через капиталоемкость продукции,
природные ресурсы, эффективный труд и
параметры модели. После этого, используя
результат задания 2, выразите ставку
процента на траектории сбалансированного
роста через параметры модели.
-
Сравните результаты пунктов 3, 4 и 5 и ответьте на вопрос: в случае, если запас капитала на траектории сбалансированного роста соответствуют золотому правилу, как соотносятся темпы экономического роста на траектории сбалансированного роста и реальная ставка процента? Является ли этот результат таким же, как в модели Солоу без природных ресурсов или же отличается от него?
|
|
ТЕОРИЯ РОСТА
Контрольная работа
ФИО _______________________________________ Группа ____________ |
Теоретическое задание.
Фундаментальные вопросы теории роста и модели роста, основанные на R&D.
Задача
Рассмотрим модель Солоу с производственной функцией Кобба-Дугласа и с человеческим капиталом. Предпосылки модели задаются следующей системой уравнений:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
где
![]() - выпуск,
- выпуск,
![]() - капитал,
- капитал,
![]() - эффективность труда,
- эффективность труда,
![]() - труд,
- труд,
![]() - эластичность выпуска по капиталу,
- эластичность выпуска по капиталу,
![]() - темп технического прогресса,
- темп технического прогресса,
![]() - темп роста населения,
- темп роста населения,
![]() - норма сбережения,
- норма сбережения,
![]() - норма износа оборудования. Известно,
что
- норма износа оборудования. Известно,
что
![]()
Пусть
![]() и
и
![]() - соответственно физический и человеческий
капитал в расчете на единицу эффективного
труда.
- соответственно физический и человеческий
капитал в расчете на единицу эффективного
труда.
Задания.
-
Представьте производственную функцию в интенсивной форме: выразите выпуск в расчете на единицу эффективного труда через физический и человеческий капитал в расчете на единицу эффективного труда.
-
Из предпосылок уравнений получите систему дифференциальных уравнений второго порядка относительно
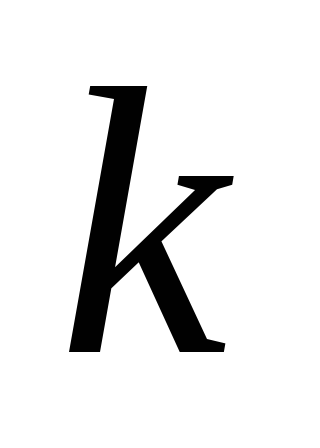 и
и
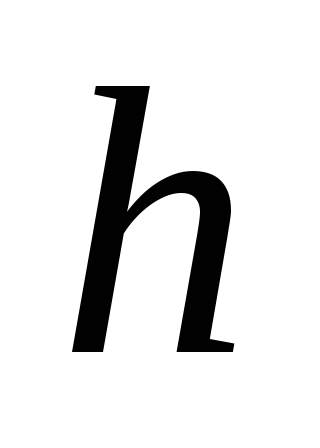 .
. -
Выразите уравнение, определяющие пары значений
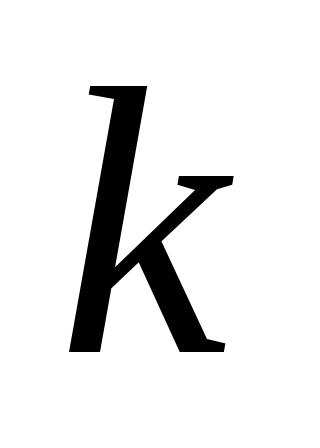 и
и
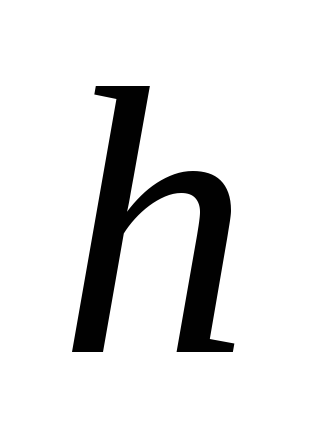 ,
для которых
,
для которых
 .
Зная, что
.
Зная, что
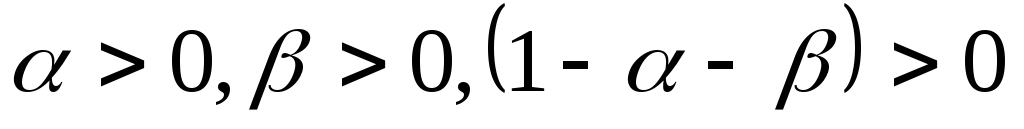 ,
определите, является ли уравнение линии
,
определите, является ли уравнение линии
 выпуклым или вогнутым в координатах
(
выпуклым или вогнутым в координатах
(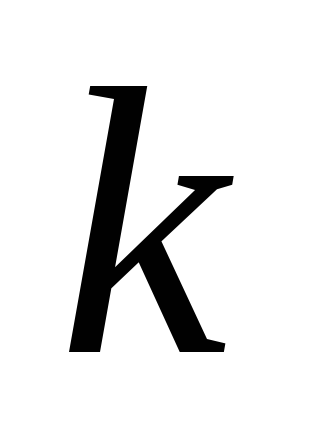 и
и
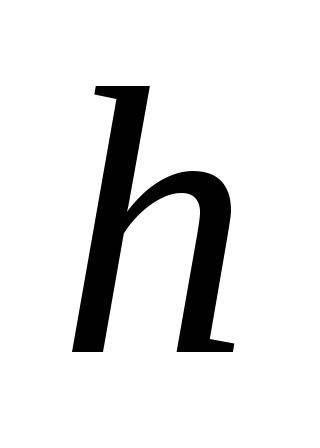 ).
Изобразите линию
).
Изобразите линию
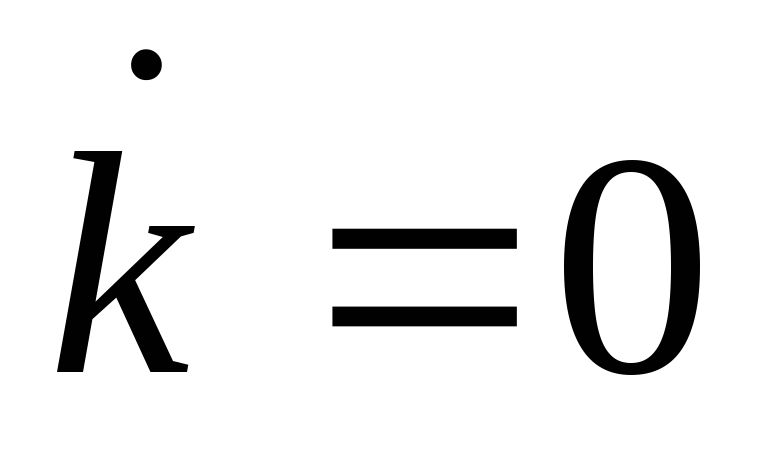 в координатах
в координатах
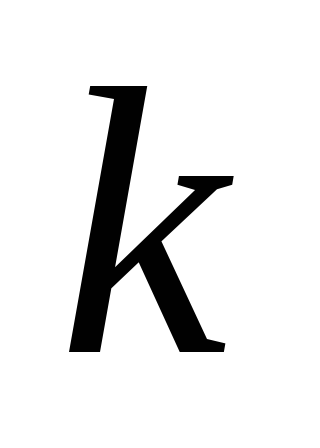 и
и
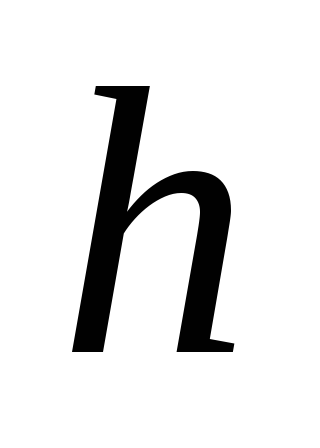 .
Пользуясь результатами задания 2,
определите, что происходит с
.
Пользуясь результатами задания 2,
определите, что происходит с
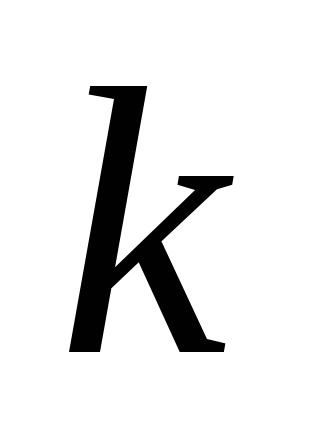 (растет или убывает), если экономика
находится выше линии
(растет или убывает), если экономика
находится выше линии
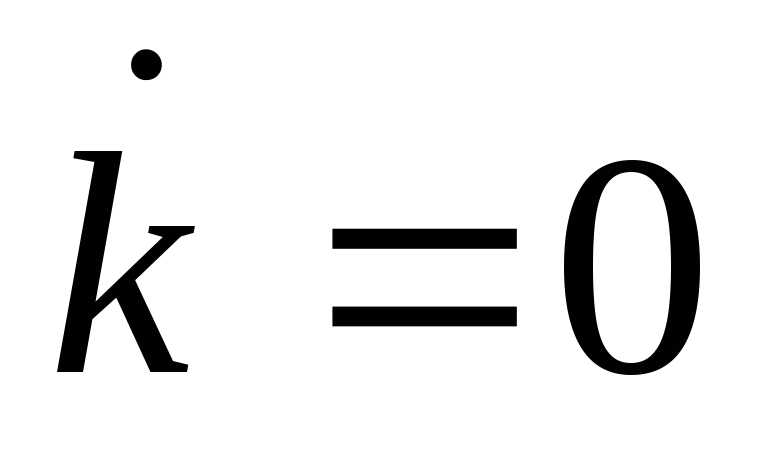 ?
Ниже?
?
Ниже? -
Аналогично заданию 3, постройте график функции
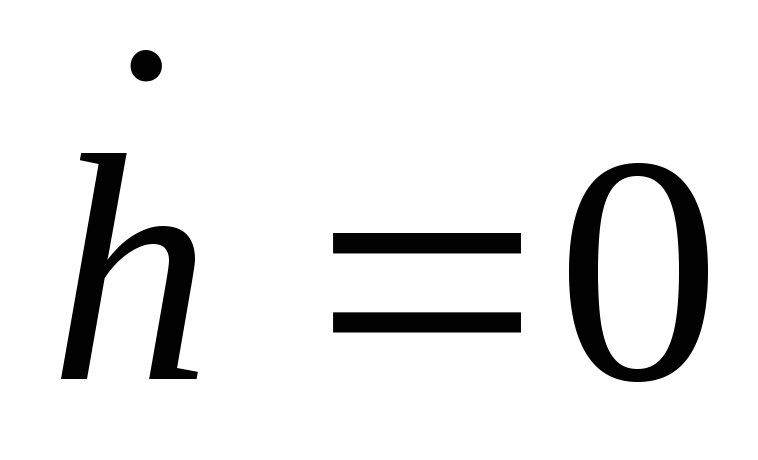 и определите, что происходит с
и определите, что происходит с
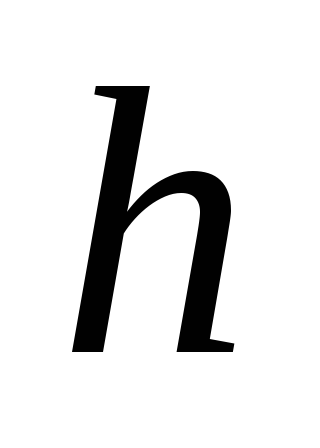 ,
если экономика находится выше или ниже
линии
,
если экономика находится выше или ниже
линии
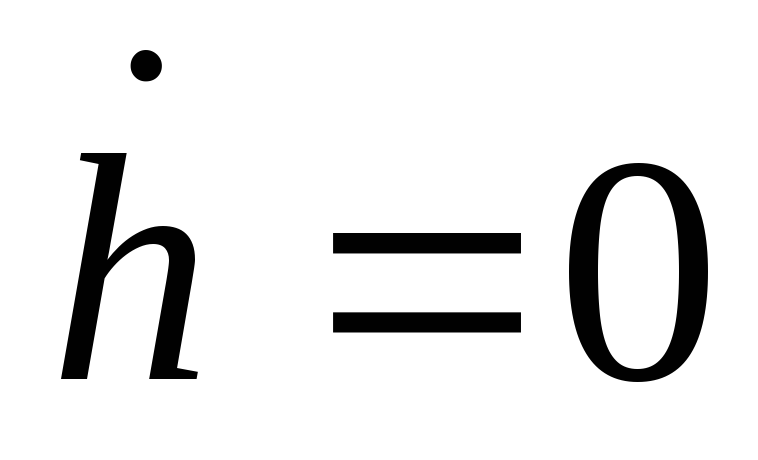 .
. -
Постройте в одной плоскости линии
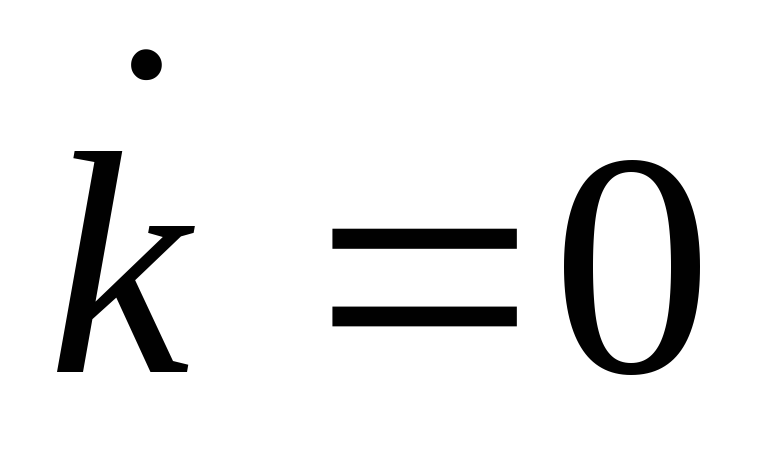 и
и
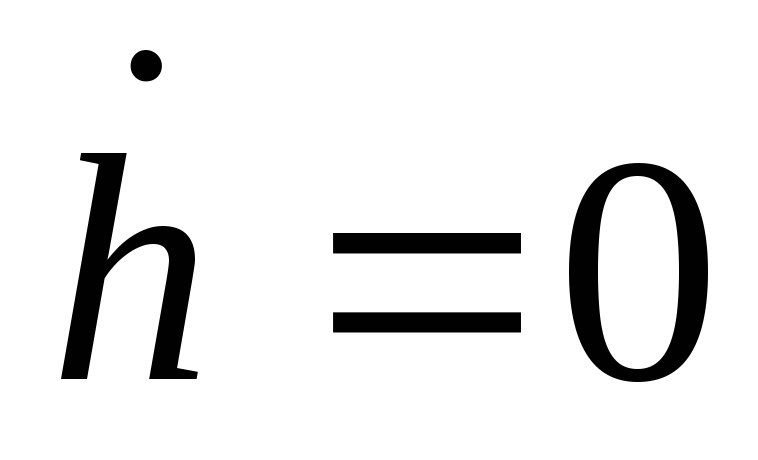 .
Покажите стрелками направления изменения
.
Покажите стрелками направления изменения
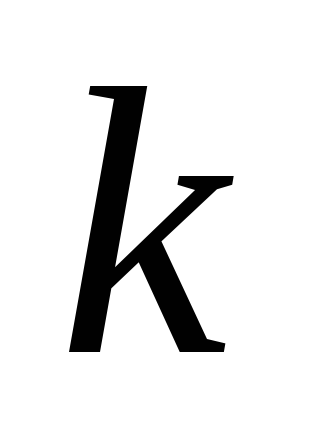 и
и
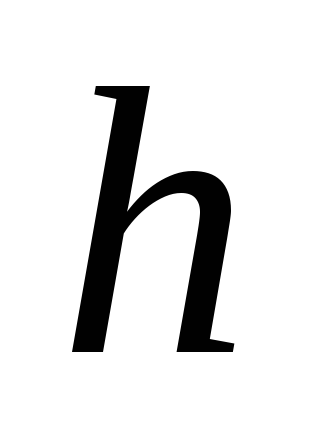 в каждой из четырех участков, на которые
разбивается плоскость линиями
в каждой из четырех участков, на которые
разбивается плоскость линиями
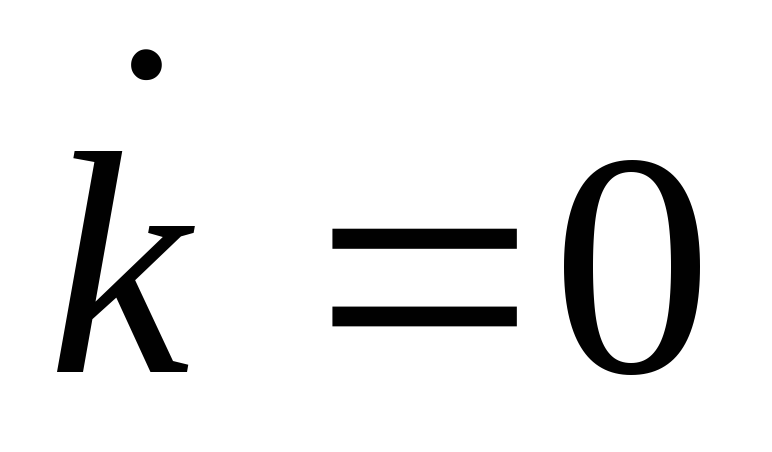 и
и
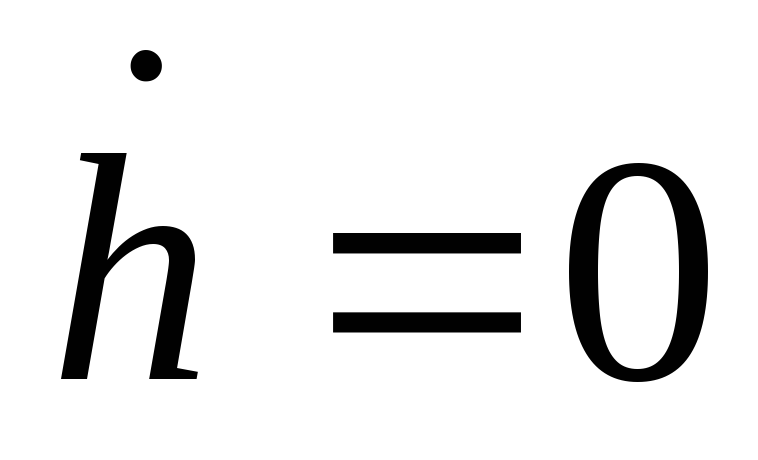 .
Изобразите несколько траекторий
динамики, которые бы показывали все
качественно различные случаи динамики
системы. Является ли траектория
сбалансированного роста локально
устойчивой?
.
Изобразите несколько траекторий
динамики, которые бы показывали все
качественно различные случаи динамики
системы. Является ли траектория
сбалансированного роста локально
устойчивой? -
Воспользуйтесь выражениями, задающими линии
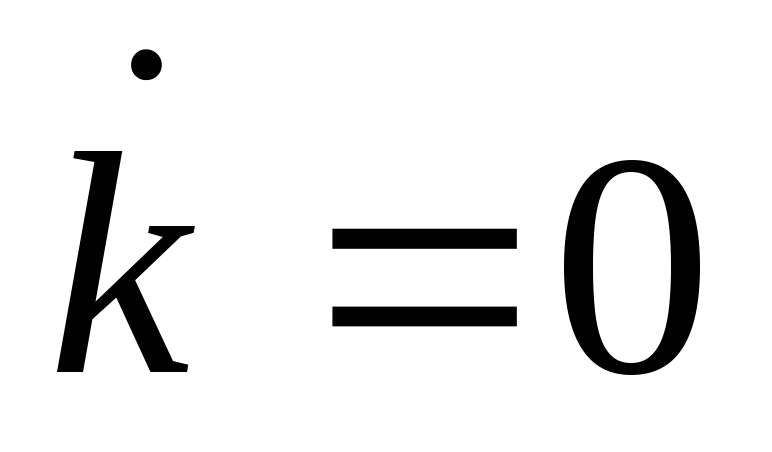 и
и
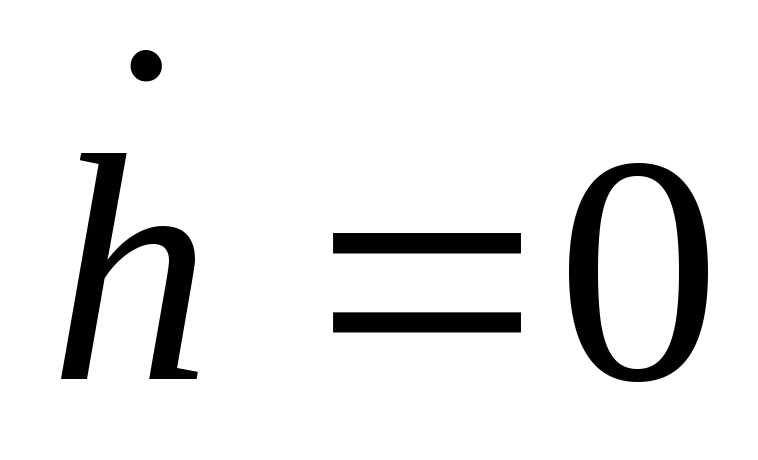 ,
и выведите из них логарифмы физического
и человеческого капитал на единицу
эффективного труда на траектории
сбалансированного роста (
,
и выведите из них логарифмы физического
и человеческого капитал на единицу
эффективного труда на траектории
сбалансированного роста (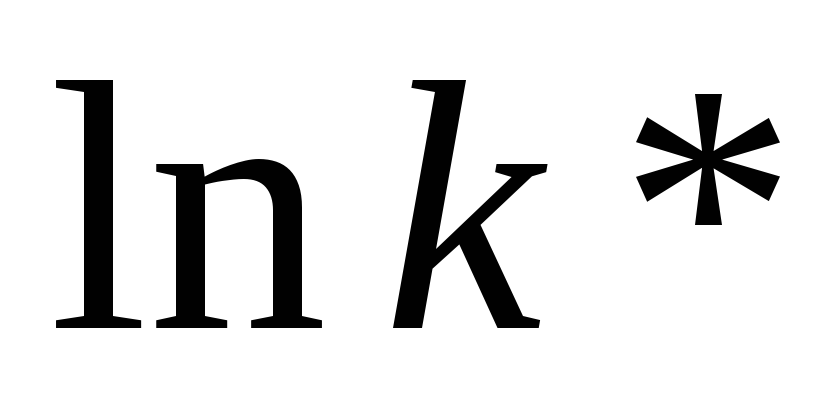 и
и
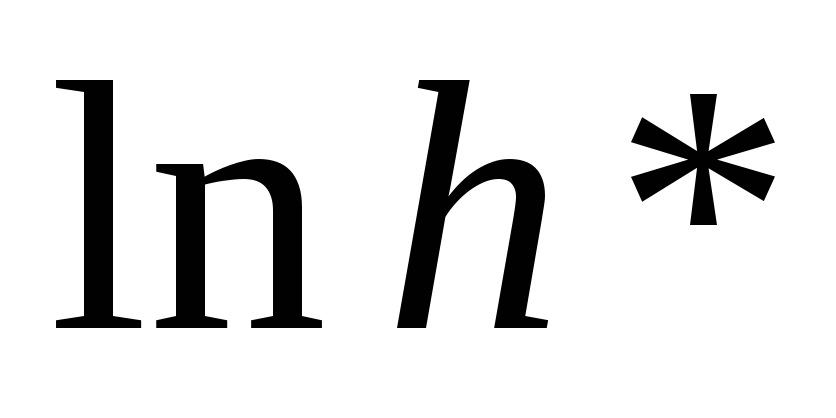 )
через параметры модели.
)
через параметры модели. -
Используя решение предыдущего задания, выразите выпуск на единицу эффективного труда на траектории сбалансированного роста (
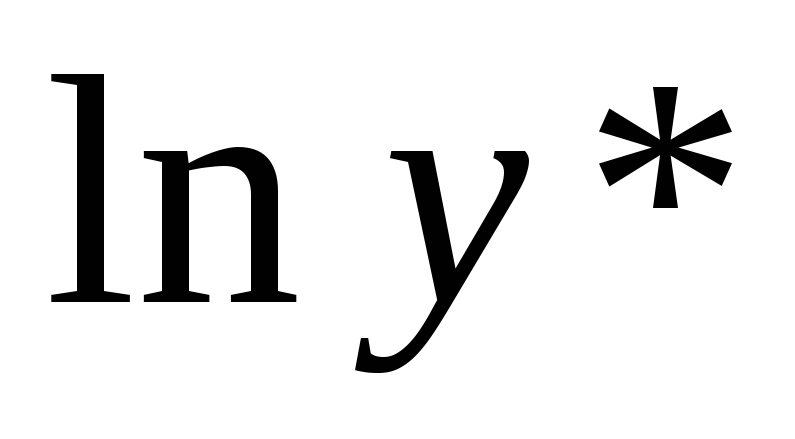 )
через параметры модели.
)
через параметры модели. -
Определите четыре следующих эластичности:
-
эластичности выпуска на единицу эффективного труда по норме сбережения в физический капитал;
-
эластичности выпуска на единицу эффективного труда по норме сбережения в человеческий капитал;
-
эластичности потребления на единицу эффективного труда по норме сбережения в физический капитал;
-
эластичности потребления на единицу эффективного труда по норме сбережения в человеческий капитал.
-
-
Определите нормы сбережений в человеческий и физический капитал, соответствующие золотому правилу.
-
Предположим, что экономика находится на траектории сбалансированного роста. Определите ставку процента и рыночную стоимость аренды единицы человеческого капитала в экономике, в которой запас капитала соответствует золотому правилу. Для этого в условия первого порядка фирм подставьте значения
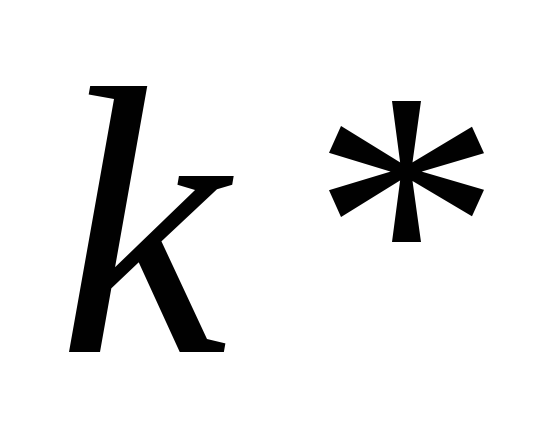 и
и
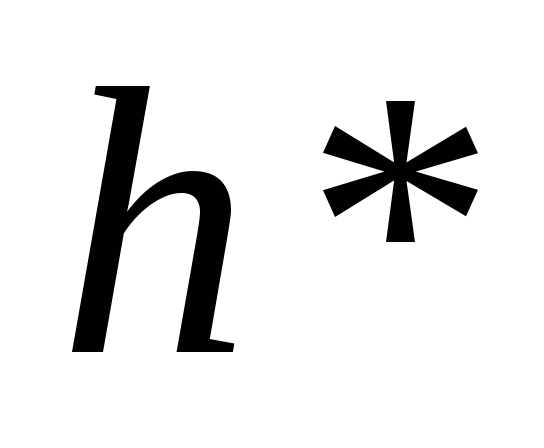 из задания 7, в которые вместо
из задания 7, в которые вместо
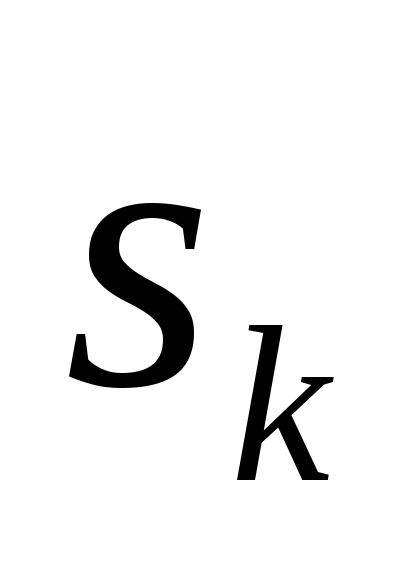 и
и
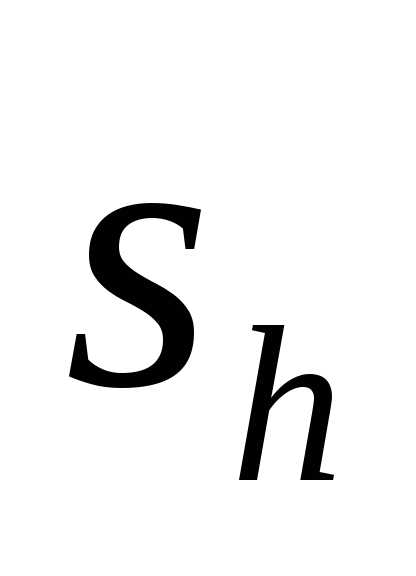 подставьте значения, найденные в задании
9. Как найденные ставка процента и
стоимость аренды капитала соотносятся
с темпами экономического роста на
траектории сбалансированного роста?
подставьте значения, найденные в задании
9. Как найденные ставка процента и
стоимость аренды капитала соотносятся
с темпами экономического роста на
траектории сбалансированного роста?
|
|
ТЕОРИЯ РОСТА
Контрольная работа
ФИО _______________________________________ Группа ____________ |
Теоретическое задание.
Фундаментальные вопросы теории роста и модель созидательного разрушения.
Задача
Одним из свойств технического прогресса
является то, что капитал, созданный к
моменту
![]() ,
зависит от уровня технологии в момент
,
зависит от уровня технологии в момент
![]() и не совершенствуется за счет будущего
технического прогресса. Эта гипотеза
известна как гипотеза воплощенного
технического прогресса (технический
прогресс должен быть «воплощен» в
капитале до того, как он приведет к росту
выпуска). В данной задаче Вам предлагается
исследовать последствия этого эффекта.
и не совершенствуется за счет будущего
технического прогресса. Эта гипотеза
известна как гипотеза воплощенного
технического прогресса (технический
прогресс должен быть «воплощен» в
капитале до того, как он приведет к росту
выпуска). В данной задаче Вам предлагается
исследовать последствия этого эффекта.
(а) Во-первых, модифицируем базовую
модель Солоу, предположив, что технический
прогресс воплощается в капитале, а не
в труде. Для того, чтобы существовала
траектория сбалансированного роста,
предположим, что производственная
функция имеет вид Кобба-Дугласа,
![]() .
Предположим, что
.
Предположим, что
![]() растет с темпом
растет с темпом
![]() :
:
![]() .
.
Покажите, что экономика стремится к
траектории сбалансированного роста, и
определите темпы роста
![]() и
и
![]() на траектории сбалансированного роста.
(Подсказка: покажите, что мы можем
записать
на траектории сбалансированного роста.
(Подсказка: покажите, что мы можем
записать
![]() как функцию от
как функцию от
![]() ,
где
,
где
![]() ,
после чего проведите анализ динамики
,
после чего проведите анализ динамики
![]() .)
.)
(б) Теперь введем гипотезу воплощенного
технического прогресса. Предположим,
что производственная функция имеет вид
![]() ,
где
,
где
![]() – эффективный запас капитала. Динамика
– эффективный запас капитала. Динамика
![]() задается выражением
задается выражением
![]() .
Множитель
.
Множитель
![]() в последнем выражении показывает, что
инвестиции в момент
в последнем выражении показывает, что
инвестиции в момент
![]() зависят от технологии в момент
зависят от технологии в момент
![]() .
.
Покажите, что экономика стремится к
траектории сбалансированного роста.
Каковы темпы роста
![]() и
и
![]() на траектории сбалансированного роста?
(Подсказка: обозначьте
на траектории сбалансированного роста?
(Подсказка: обозначьте
![]() ,
после чего воспользуйтесь тем же
подходом, что и в пункте (а), анализируя
динамику
,
после чего воспользуйтесь тем же
подходом, что и в пункте (а), анализируя
динамику
![]() вместо
вместо
![]() ).
).
(в) Какова эластичность выпуска по
![]() на
траектории сбалансированного роста?
на
траектории сбалансированного роста?
(г) Какова скорость сходимости к траектории сбалансированного роста в ее окрестности?
(д) Сравните результаты пунктов (в) и (г) с соответствующими результатами в модели Солоу.
|
|
ТЕОРИЯ РОСТА
Контрольная работа
ФИО _______________________________________ Группа ____________ |
Теоретическое задание.
Фундаментальные вопросы теории роста и модель распространения идей, предложенная Лукасом.
Задача
3.6. Производственная функция
Этьера. (Этьер, 1982). Пусть производственная
функция имеет вид
![]() , где
, где
![]() это используемое количество капитального
блага
это используемое количество капитального
блага
![]() ,
а
,
а
![]() измеряет диапазон потенциальных
капитальных благ.
измеряет диапазон потенциальных
капитальных благ.
(а) Пусть
![]() равно
равно
![]() для
для
![]() и равно нулю в других случаях. Найдите
и равно нулю в других случаях. Найдите
![]() как функцию от
как функцию от
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
(b) Пусть арендная плата за капитальное
благо
![]() равна
равна
![]() ,
а заработная плата равна
,
а заработная плата равна
![]() .
Рассмотрим фирму, стремящуюся произвести
1 единицу выпуска с минимальными
затратами.
.
Рассмотрим фирму, стремящуюся произвести
1 единицу выпуска с минимальными
затратами.
(i) Постройте функцию Лагранжа для задачи минимизации фирмы.
(ii) Найдите условие первого порядка
для
![]() .
.
(iii) Покажите, что из условия первого
порядка следует, что эластичность спроса
на капитальное благо
![]() равна
равна
![]() .
(Обратите внимание, что поскольку цена
монополиста, максимизирующего прибыль,
равна произведению
.
(Обратите внимание, что поскольку цена
монополиста, максимизирующего прибыль,
равна произведению
![]() и издержек, то прибыль монополиста-поставщика
капитального блага
и издержек, то прибыль монополиста-поставщика
капитального блага
![]() при максимизирующей прибыль цене равна
при максимизирующей прибыль цене равна
![]() или
или
![]() ,
где
,
где
![]() - максимизирующая прибыль цена капитального
блага
- максимизирующая прибыль цена капитального
блага
![]() ,
а
,
а
![]() - величина спроса при этой цене).
- величина спроса при этой цене).
|
|
ТЕОРИЯ РОСТА
Контрольная работа
ФИО _______________________________________ Группа ____________ |
Теоретическое задание.
Ответьте на следующие два вопроса:
-
Концепция, лежащая в основе моделей эндогенного роста.
-
Критика Джонса моделей, основанных на R&D.
Задача
Рассмотрим производственную функцию
вида
![]() .
Предположим, что в экономике наблюдается
несовершенная конкуренция, при этом
спрос на продукцию одной фирмы имеет
эластичность, равную
.
Предположим, что в экономике наблюдается
несовершенная конкуренция, при этом
спрос на продукцию одной фирмы имеет
эластичность, равную
![]() .
.
Введем следующие обозначения:
![]() - доли расходов соответственно на
капитал, на труд и на промежуточную
продукцию в общих расходах;
- доли расходов соответственно на
капитал, на труд и на промежуточную
продукцию в общих расходах;
![]() - доли доходов капитала, труда, промежуточной
продукции и доля прибыли в общих доходах;
- доли доходов капитала, труда, промежуточной
продукции и доля прибыли в общих доходах;
![]() - отдача от масштаба;
- отдача от масштаба;
![]() - доля наценки в цене
- доля наценки в цене
![]() .
.
Задания.
-
Покажите, что если производственная функция описывается постоянной отдачей от масштаба, в экономике наблюдается совершенная конкуренция, при этом технический прогресс нейтрален по Хиксу, то
![]() ,
,
где
![]() - доли доходов труда и капитала в общем
доходе.
- доли доходов труда и капитала в общем
доходе.
-
Выведите уравнение, связывающее между собой наценку фирм и эластичность спроса на продукцию одной фирмы. Выведите уравнение, связывающее между собой отдачу от масштаба, наценку и долю прибыли в ВВП.
Подсказка
1: для определения размера наценки
следует решить задачу максимизации
прибыли вида
![]() ,
а для определения доли прибыли в ВВП –
задачу вида
,
а для определения доли прибыли в ВВП –
задачу вида
![]() .
Подсказка
2: будьте аккуратны с нормализацией цен.
Нормализацию следует проводить после
нахождения
условий первого порядка задачи фирмы.
.
Подсказка
2: будьте аккуратны с нормализацией цен.
Нормализацию следует проводить после
нахождения
условий первого порядка задачи фирмы.
-
Базу и Фернальд оценивают долю прибыли в ВВП в 3%, а однородность производственной функции в 101%. Каков средний размер наценки?
-
Пусть технология производства одной фирмой задается уравнением
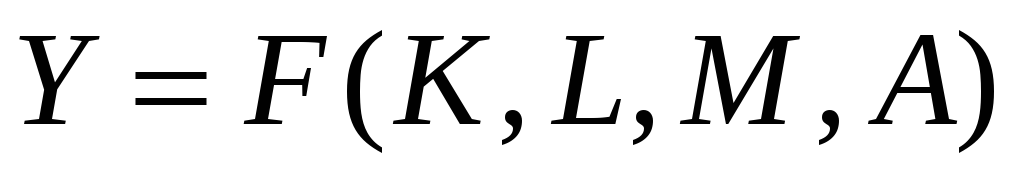 ,
где М – промежуточная продукция.
Покажите, что в случае нейтральности
по Хиксу технического прогресса,
несовершенной конкуренции и непостоянной
отдачи от масштаба, мы можем записать:
,
где М – промежуточная продукция.
Покажите, что в случае нейтральности
по Хиксу технического прогресса,
несовершенной конкуренции и непостоянной
отдачи от масштаба, мы можем записать:
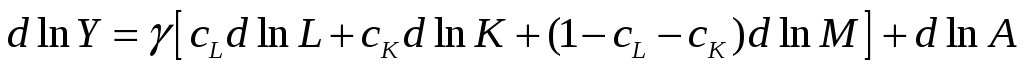 ,
где
,
где
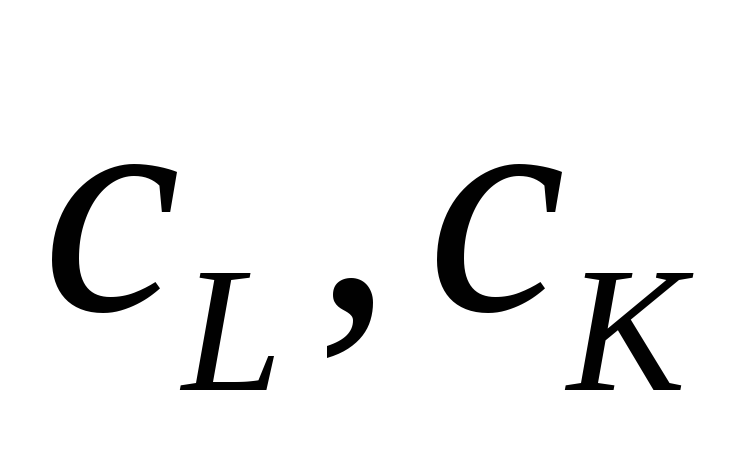 - доли расходов на труд и на капитал в
общих расходах.
- доли расходов на труд и на капитал в
общих расходах.
-
Покажите, как связаны между собой доли доходов
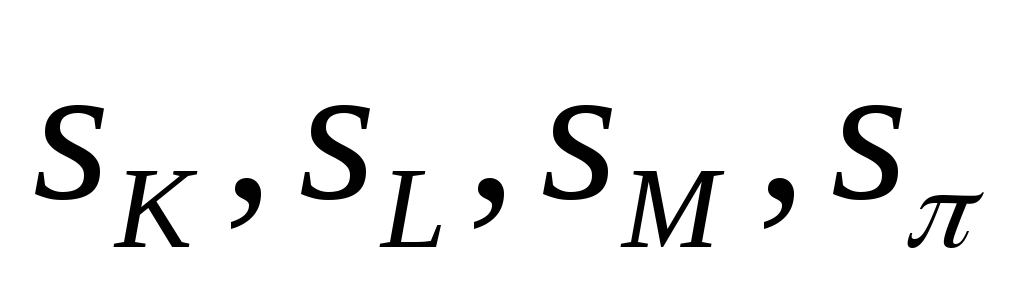 и доли расходов
и доли расходов
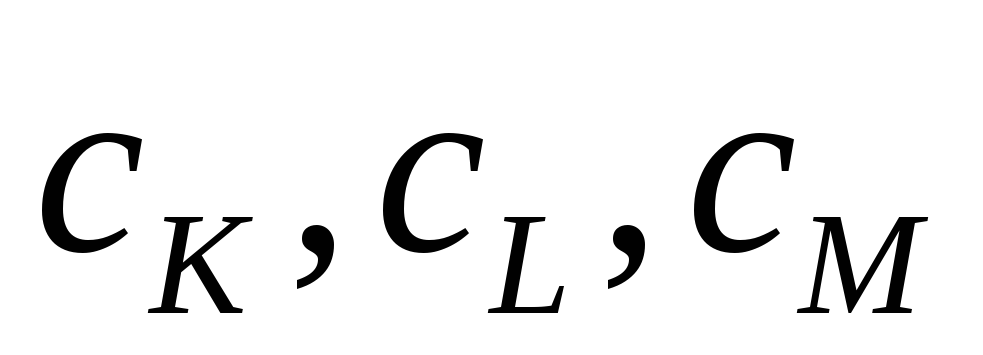 .
.





