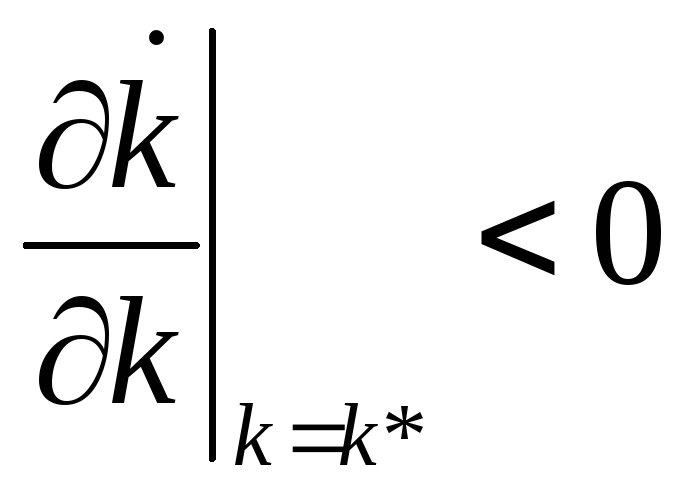Арефьев н.Г. ©

Лекция 2

Введение в теорию роста.

Модель Солоу

Содержание

1. Введение в неоклассическую теорию экономического роста:

технический анализ

1.1. Базовые предпосылки относительно производственной функции

1.2. Вывод основного уравнения динамики

1.3. Модель Солоу (технический анализ)

1.4. Траектория сбалансированного роста

1.5. Воздействие изменения нормы сбережений на капитал, выпуск

и потребление на траектории сбалансированного роста.

Золотое правило запаса капитала

1.6. Динамика модели, вызванная изменением нормы сбережений

1.7. Конвергенция (технический анализ)

1.8. Производственная функция Кобба-Дугласа в модели Солоу

2. Введение в неоклассическую теорию экономического роста:

эмпирические исследования и фундаментальные вопросы

2.1. Историческая справка

2.2. Конвергенция

2.3. Фундаментальные вопросы теории роста

2.4. История развития теории экономического роста

3. Модель Солоу

3.1. Базовые предпосылки

3.2. Оценка качества модели Солоу

3.3. Фундаментальные вопросы и модель Солоу

3.4. Природные ресурсы в модели Солоу

3.5. Эмпирические исследования, связанные с моделью Солоу

Приложение 1. Анализ конвергенции в статье Баумоля (1986)

Приложение 2. Анализ конвергенции в статье Де Лонга (1988)

1. Введение в неоклассическую теорию экономического роста:

материал для разбора на семинарах¹

1.1. Базовые предпосылки относительно производственной функции

Основное завоевание неоклассической теории роста – это без сомнений неоклассическая производственная функция; все значимые результаты получены исключительно благодаря её введению.

производственная функция, нейтральная по Харроду (в соответствии с классификацией в учебнике Ромера)

постоянная отдача от масштаба (1)

Предполагается, что производственная функция обладает стандартными неоклассическими свойствами (убывающая предельная полезность каждого из факторов, положительная эластичность замещения).

1.2. Вывод основного уравнения динамики

Для того, что бы получить производственную функцию в интенсивной форме, нужно воспользоваться свойством постоянной отдачи от масштаба. Подставив в (1) λ= 1/AL, получаем:

Сделав замену y=Y/AL – выпуск в расчете на единицу эффективного труда ,f(k) =F(K/AL,1) =F(K,AL)/AL, получаем производственную функцию в интенсивной форме

.

Преимущество перед экстенсивной формой записи в том, что это функция от одной переменной, т.е. мы можем перейти от трехмерного анализа к двумерному.

Найдем динамику капиталовооруженности эффективного труда

(2)

где ,задаются экзогенно

Введем переменную C, которая может рассматриваться как а) потребление б) частное потребление плюс госрасходы.c=C/AL - потребление на единицу эффективного труда.

Подставляя выражение динамики капитала, или по-другому, выражение, определяющие величину чистых инвестиций

в уравнение (2), получаем основное уравнение динамики неоклассической теории роста

(3)

Это уравнение будет использоваться как в модели Солоу, так и в других моделях неоклассической теории роста.

1.3. Модель Солоу

Задавая экзогенно норму сбережений s= (1 –C/Y), получаем основное уравнение динамики модели Солоу.

(4)

Если производственная функция в экстенсивной форме обладает свойством убывающей предельной производительности капитала, тогда производственная функция будет обладать свойством убывающей предельной производительности капиталовооруженности эффективного труда

(самостоятельно покажите, как связаны производные производственных функций в интенсивной и экстенсивной формах)

Условия Инады являются достаточными (но не необходимыми) условиями существования траектории сбалансированного роста

,

Динамику kможно анализировать, используя, например, диаграмму Солоу (см. рис. 1а) или фазовую диаграмму (рис. 1б).

Еслиk <k*, тогдаkвозрастает,

Если k >k*, тогдаkснижается,

Если k =k*, тогдаkпостоянна.

 k=k*является точкой устойчивого равновесия

k= 0 является точкой неустойчивого равновесия

Диаграма Солоу и Фазовая диаграма – два эквивалентных способа анализа точек равновесия и устойчивости системы. Для модели Солоу удобней диаграма Солоу; фазовую диаграму тоже нужно знать, так как она будет встречаться в других моделях.

Устойчивость системы можно так же продемонстрировать, взяв производную в точке равновесия. Что бы система была устойчивой, эта производная должна быть отрицательной, это очевидно из анализа на фазовой плоскости.