Макро Арефьев с хсехелп / 1variant
.pdf
Теория экономического роста Контрольная работа
ФИО _____________________________________________________________ Группа ________________
(1 балл – за разборчивый подчерк и заполненную графу вверху)
Задание 1 (1 балл).
Экономика описывается моделью Солоу с производственной функцией Кобба-Дугласа и находится на траектории сбалансированного роста. Заполните в таблице внизу все клетки, которые можно заполнить, основываясь на информации из других клеток. Если для заполнения какойто клетки информации недостаточно, она должна оставаться незаполненной.
|
Темп технического прогресса |
|
3% |
|
|
Темп прироста населения |
|
2% |
|
|
Норма амортизации |
|
3% |
|
|
Норма сбережений |
|
|
|
|
Доля дохода капитала |
|
1/3 |
|
|
Темп прироста агрегированного выпуска |
|
|
|
|
Темп прироста потребления на душу населения |
|
|
|
|
Темп прироста капиталовооруженности труда |
|
|
|
|
Реальная ставка процента |
|
|
|
|
Решение: |
|
|
|
|
Темп технического прогресса |
|
3% |
|
|
|
|
||
|
Темп прироста населения |
|
2% |
|
|
Норма амортизации |
|
3% |
|
|
Норма сбережений |
|
|
|
|
Доля дохода капитала |
|
1/3 |
|
|
|
|
5% |
|
|
Темп прироста агрегированного выпуска |
|
3% |
|
|
Темп прироста потребления на душу населения |
|
3% |
|
|
Темп прироста капиталовооруженности труда |
|
|
|
|
Реальная ставка процента |
|
|
|
|
Критерии оценок: |
|
|
|
|
0 ошибок – 1 балл |
|
|
|
|
1 ошибка – 0.5 балла |
|
|
|
|
2 ошибки и более – 0 баллов. |
|
|
|
Задание 2 (3 балла).
Экономика описывается моделью Солоу и находится на траектории сбалансированного роста. Происходит дискретное снижение численности рабочей силы, после чего рабочая сила растет с прежним темпом. Изобразите этот шок на диаграмме Солоу, а также покажите, какая будет наблюдаться динамика заработной платы эффективного труда, логарифма
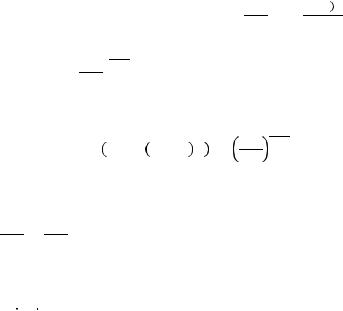
подушевого потребления, логарифма выпуска, темпов прироста выпуска и ставки процента.
Критерии оценок:
Каждый график оценивается в 0.5 балла
Задание 3 (3 балла).
Рассмотрим модель перекрывающихся поколений с логарифмической функцией полезности и производственной функцией Кобба-Дугласа. Определите, при каких параметрах модели запас капитала, соответствующий траектории сбалансированного роста, равен запасу капитала, соответствующему золотому правилу запаса капитала.
Решение:
Уравнение накопления капитала в модели с производственной функцией Кобба-Дугласа и логарифмической функцией полезности:
(1 балл)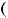 
1 +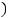 
!!! = 
!
, 
!!!
= !!!! = 
!!!!!!! !!
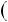
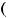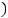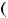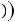На траектории сбалансированного роста:
!
(0.5 балла) =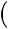 
!!!!!! !!!! 
!!!
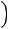Запас капитала, соответствующий золотому правилу, определяется из следующей задачи максимизации
|
|
! |
||
(1 балл) |
!" = arg max ! − |
1 + = |
!!!! |
!!! |
Таким образом, запас капитала на траектории сбалансированного роста совпадает с запасом капитала, соответствующем золотому правилу, при следующем соотношении параметров:
(0.5 балла) !!!! = !!!!
Задание 4 (2 балла).
В рамках модели Mankiw, Romer, Weil постройте фазовую плоскость в координатах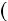 
, 
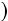. Исследуйте на этой фазовой плоскости устойчивость системы.