Макро Арефьев с хсехелп / Решенный вариант 5
.docВариант 1. Рассмотрим модель Солоу с производственной функцией Кобба-Дугласа и с природными ресурсами. Предпосылки модели задаются следующей системой уравнений:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
где
![]() - выпуск,
- выпуск,
![]() - капитал,
- капитал,
![]() - эффективность труда,
- эффективность труда,
![]() - труд,
- труд,
![]() - природные ресурсы,
- природные ресурсы,
![]() - эластичность выпуска по капиталу,
- эластичность выпуска по капиталу,
![]() - темп технического прогресса,
- темп технического прогресса,
![]() - темп роста населения,
- темп роста населения,
![]() - темп выбытия природных ресурсов,
- темп выбытия природных ресурсов,
![]() - норма сбережения,
- норма сбережения,
![]() - норма износа оборудования.
- норма износа оборудования.
Пусть
![]() - капиталоемкость продукции,
- капиталоемкость продукции,
![]() .
.
Задания.
-
Из гипотез модели выразите линейное дифференциальное уравнение относительно капиталоемкости продукции. Решите это уравнение.
-
Используя решение, полученное в предыдущем пункте задачи, определите, к чему стремится капиталоемкость продукции на траектории сбалансированного роста через параметры модели.
-
Выразите выпуск на траектории сбалансированного роста через капиталоемкость продукции на траектории сбалансированного роста. Из полученного выражения определите темпы роста экономики на траектории сбалансированного роста.
-
Выразите потребление на момент
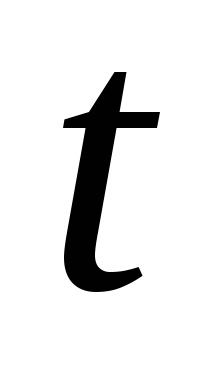 через капиталоемкость продукции на
момент
через капиталоемкость продукции на
момент
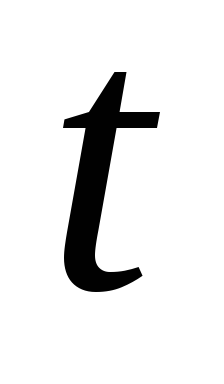 ,
эффективный труд на момент
,
эффективный труд на момент
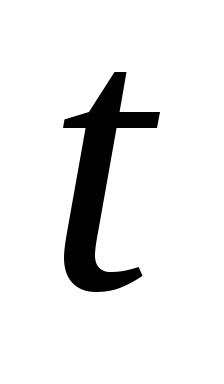 и параметры модели. Используя выражение
для капиталоемкости продукции на
траектории сбалансированного роста,
определите норму сбережения,
соответствующую золотому правилу. Как
норма сбережений, соответствующая
золотому правилу в модели Солоу с
природными ресурсами соотносится с
нормой сбережений, соответствующей
золотому правилу в модели Солоу без
природных ресурсов?
и параметры модели. Используя выражение
для капиталоемкости продукции на
траектории сбалансированного роста,
определите норму сбережения,
соответствующую золотому правилу. Как
норма сбережений, соответствующая
золотому правилу в модели Солоу с
природными ресурсами соотносится с
нормой сбережений, соответствующей
золотому правилу в модели Солоу без
природных ресурсов? -
Из условий максимизации прибыли фирмой, выразите ставку процента через капитал, природные ресурсы, эффективный труд и параметры модели. Затем подставьте
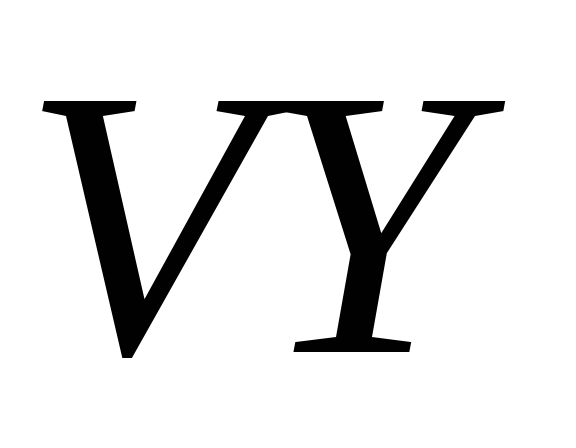 вместо
вместо
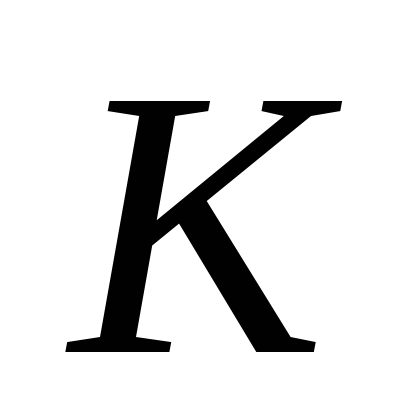 ,
,
 из пункта 3, и выразите ставку процента
через капиталоемкость продукции,
природные ресурсы, эффективный труд и
параметры модели. После этого, используя
результат задания 2, выразите ставку
процента на траектории сбалансированного
роста через параметры модели.
из пункта 3, и выразите ставку процента
через капиталоемкость продукции,
природные ресурсы, эффективный труд и
параметры модели. После этого, используя
результат задания 2, выразите ставку
процента на траектории сбалансированного
роста через параметры модели.
-
Сравните результаты пунктов 3, 4 и 5 и ответьте на вопрос: в случае, если запас капитала на траектории сбалансированного роста соответствуют золотому правилу, как соотносятся темпы экономического роста на траектории сбалансированного роста и реальная ставка процента? Является ли этот результат таким же, как в модели Солоу без природных ресурсов или же отличается от него?
Решение.
1.
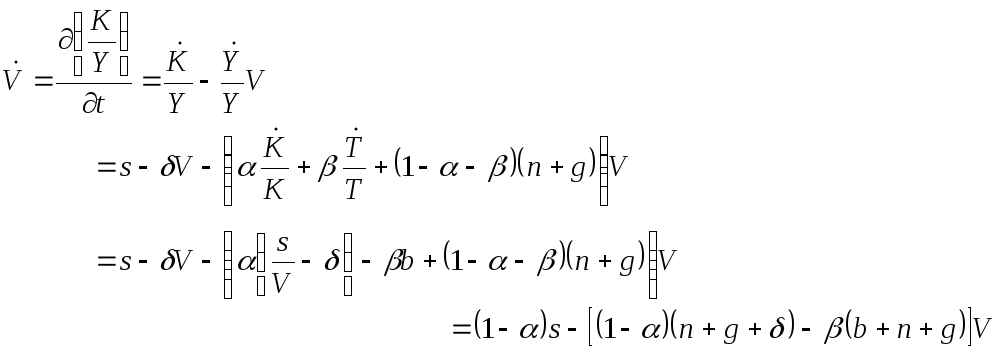
Таким образом,
![]()
Данное выражение представляет собой линейное дифференциальное уравнение относительно капиталоемкости продукции. Его решение имеет следующий вид:
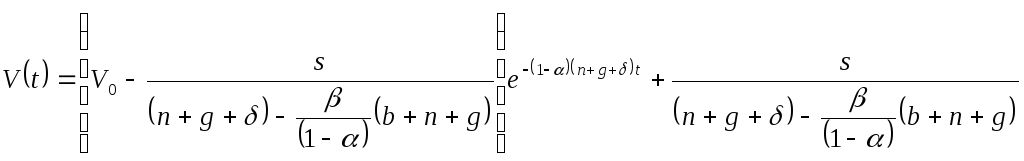
2. По мере того, как экономика стремиться к траектории сбалансированного роста, роль начальных значений сходит на нет, и первое слагаемое в полученном выражении стремиться к нулю. На траектории сбалансированного роста имеем:
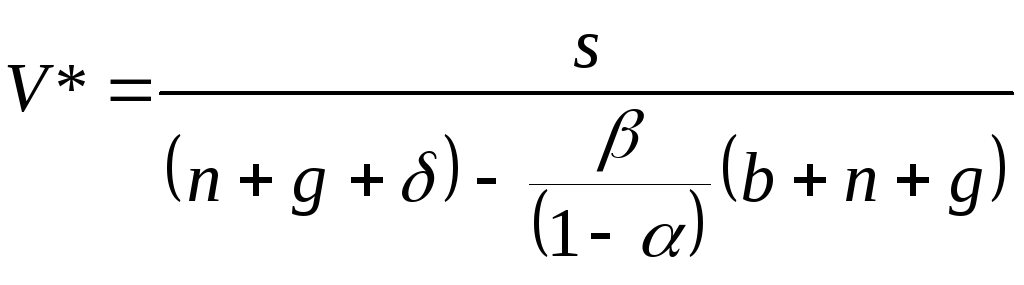
3. Подставляя в производственную функцию
![]() ,
получаем:
,
получаем:
![]() ,
,
откуда выражаем
![]() .
.
Подставляя в это выражение уравнение,
полученное в задании 2 для
![]() ,
имеем:
,
имеем:
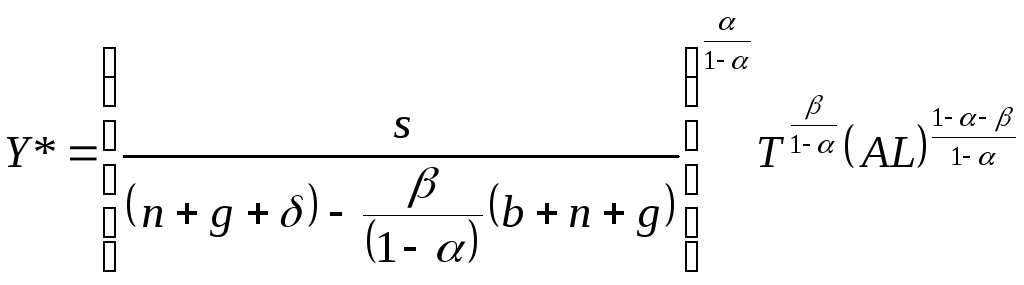 .
.
Взяв лог-производную от этого выражения по времени, получаем темпы экономического роста на траектории сбалансированного роста:
![]()
4. Используем выражение для выпуска, полученное в предыдущем пункте задачи.
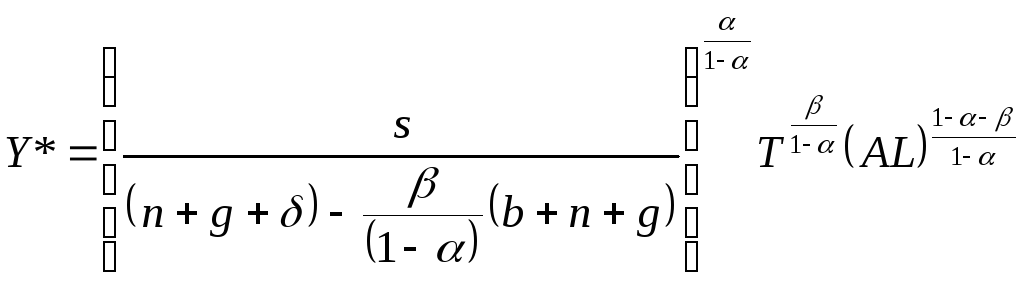
Откуда находим потребление на траектории сбалансированного роста:
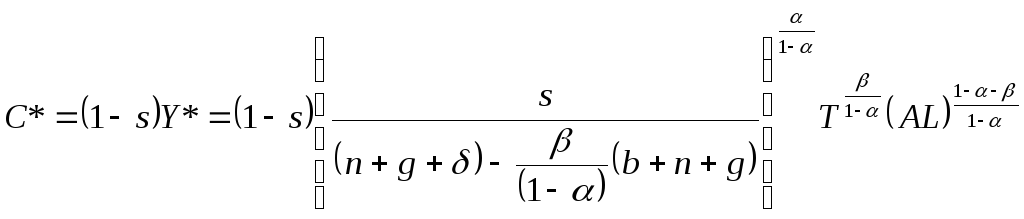 .
.
Максимизация
![]() по
по
![]() дает такое же условие для нормы сбережений,
соответствующей золотому правилу, как
и модель Солоу без природных ресурсов:
дает такое же условие для нормы сбережений,
соответствующей золотому правилу, как
и модель Солоу без природных ресурсов:
![]()
5. Из условий максимизации прибыли фирмой:
![]()
Подставляя в это выражение
![]() ,
получаем:
,
получаем:
![]()
Из задания 3
![]() .
Следовательно,
.
Следовательно,
![]()
Подставляя
![]() из задания 2, получаем:
из задания 2, получаем:
![]()
6. Если запас капитала на траектории
сбалансированного роста соответствует
золотому правилу, то из задания 4 следует
![]() ,
а из задания 5
,
а из задания 5
![]()
Сравнивая это выражение с выражением, полученным в задании 3, получаем:
![]()
Таким образом, мы получаем то же условие для запаса капитала, соответствующего золотому правилу, что и в модели Солоу без природных ресурсов: реальная ставка процента равна темпам экономического роста.
Вариант 2. Рассмотрим модель Солоу с производственной функцией Кобба-Дугласа и с человеческим капиталом. Предпосылки модели задаются следующей системой уравнений:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
где
![]() - выпуск,
- выпуск,
![]() - капитал,
- капитал,
![]() - эффективность труда,
- эффективность труда,
![]() - труд,
- труд,
![]() - эластичность выпуска по капиталу,
- эластичность выпуска по капиталу,
![]() - темп технического прогресса,
- темп технического прогресса,
![]() - темп роста населения,
- темп роста населения,
![]() - норма сбережения,
- норма сбережения,
![]() - норма износа оборудования. Известно,
что
- норма износа оборудования. Известно,
что
![]()
Пусть
![]() и
и
![]() - соответственно физический и человеческий
капитал в расчете на единицу эффективного
труда.
- соответственно физический и человеческий
капитал в расчете на единицу эффективного
труда.
Задания.
-
Представьте производственную функцию в интенсивной форме: выразите выпуск в расчете на единицу эффективного труда через физический и человеческий капитал в расчете на единицу эффективного труда.
-
Из предпосылок уравнений получите систему дифференциальных уравнений второго порядка относительно
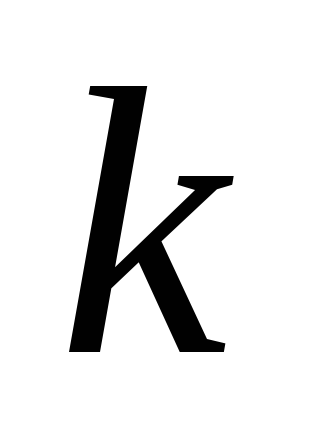 и
и
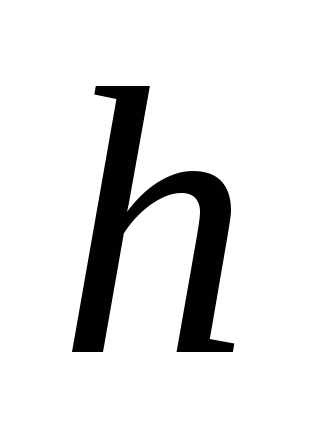 .
. -
Выразите уравнение, определяющие пары значений
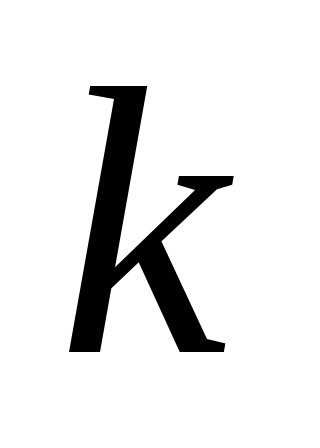 и
и
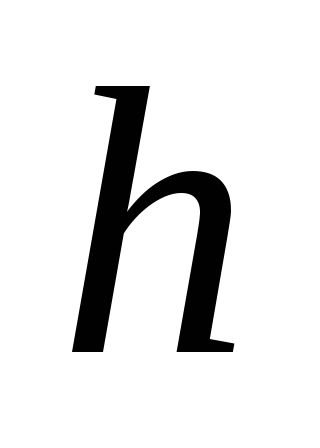 ,
для которых
,
для которых
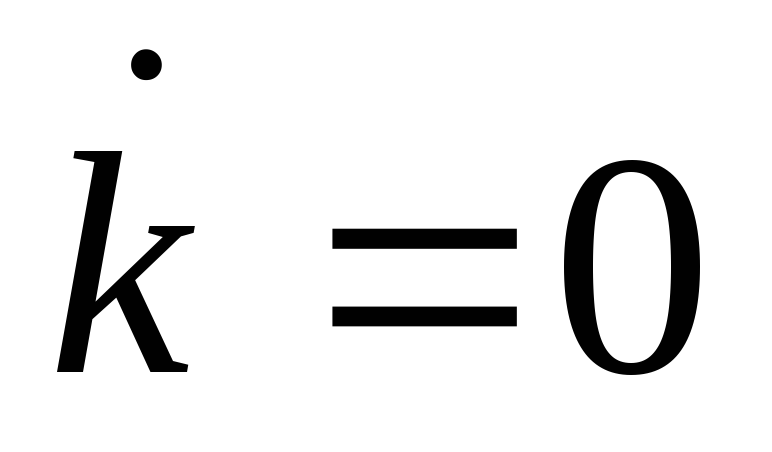 .
Зная, что
.
Зная, что
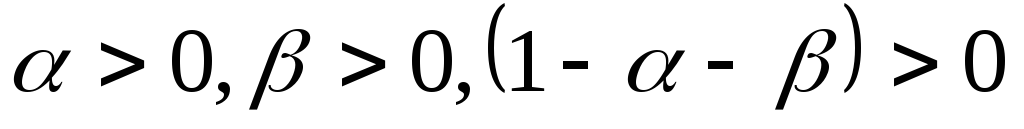 ,
определите, является ли уравнение линии
,
определите, является ли уравнение линии
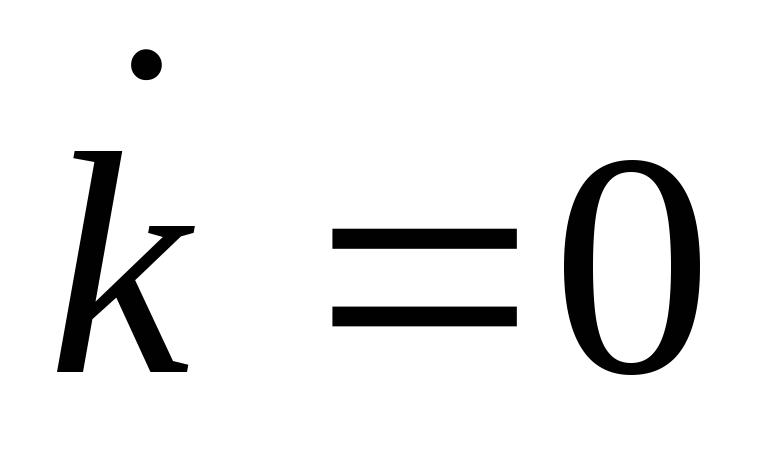 выпуклым или вогнутым в координатах
(
выпуклым или вогнутым в координатах
(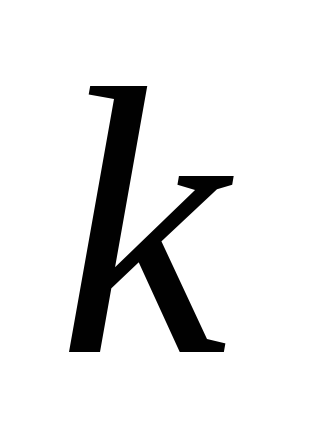 и
и
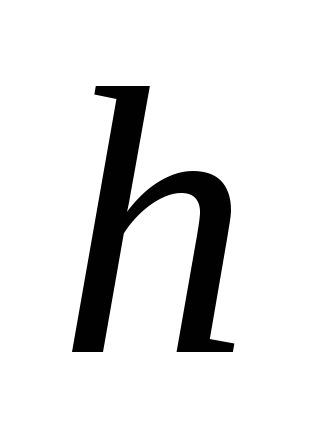 ).
Изобразите линию
).
Изобразите линию
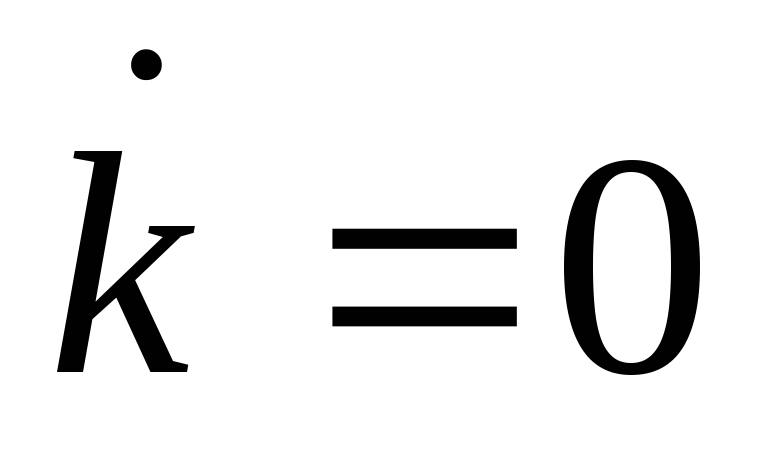 в координатах
в координатах
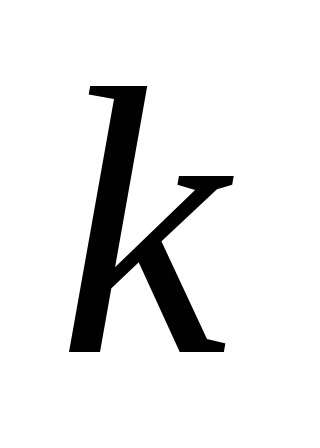 и
и
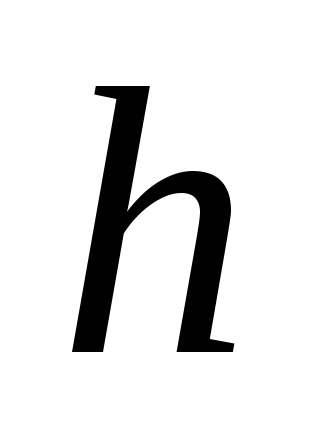 .
Пользуясь результатами задания 2,
определите, что происходит с
.
Пользуясь результатами задания 2,
определите, что происходит с
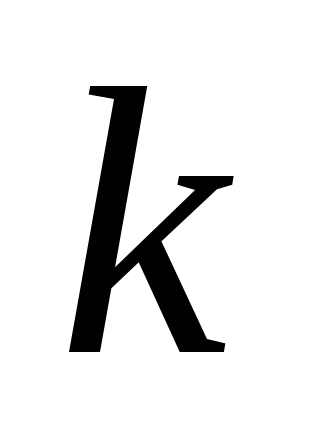 (растет или убывает), если экономика
находится выше линии
(растет или убывает), если экономика
находится выше линии
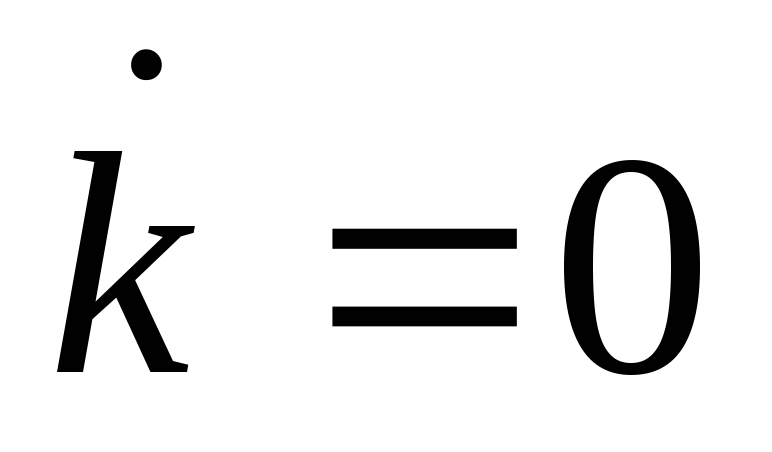 ?
Ниже?
?
Ниже? -
Аналогично заданию 3, постройте график функции
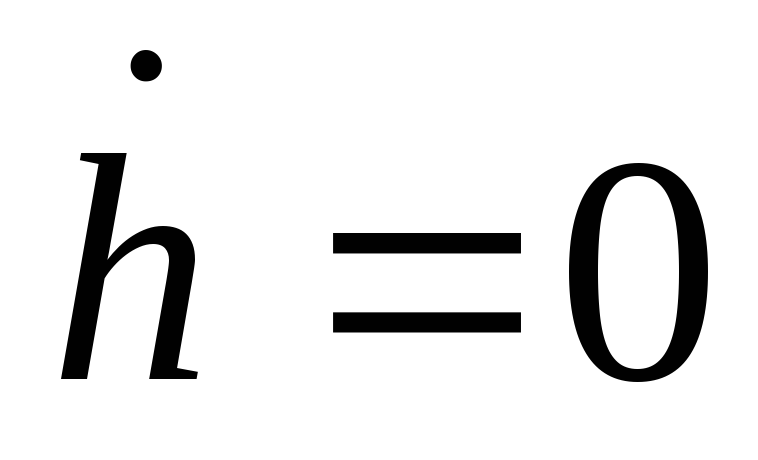 и определите, что происходит с
и определите, что происходит с
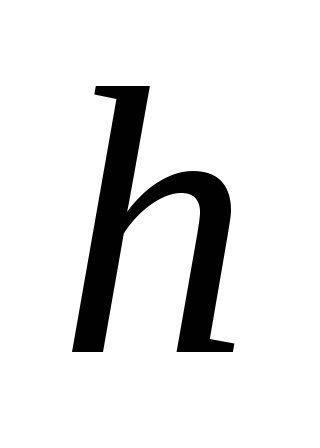 ,
если экономика находится выше или ниже
линии
,
если экономика находится выше или ниже
линии
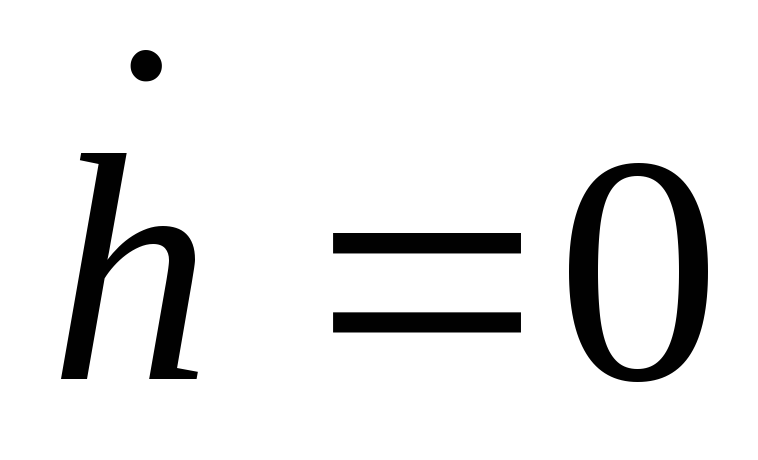 .
. -
Постройте в одной плоскости линии
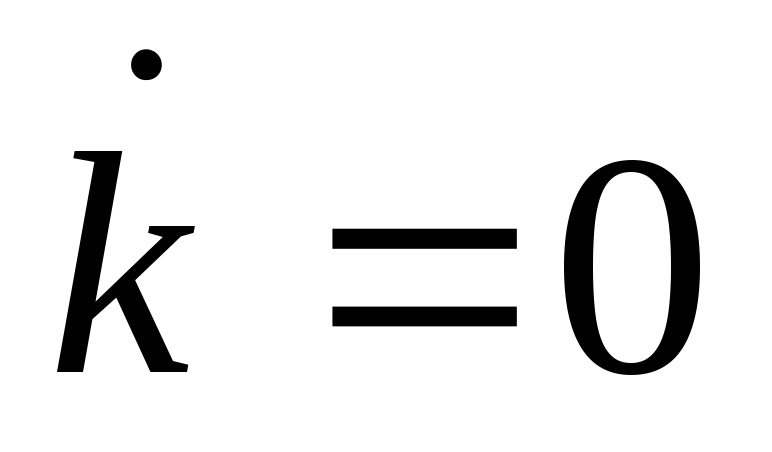 и
и
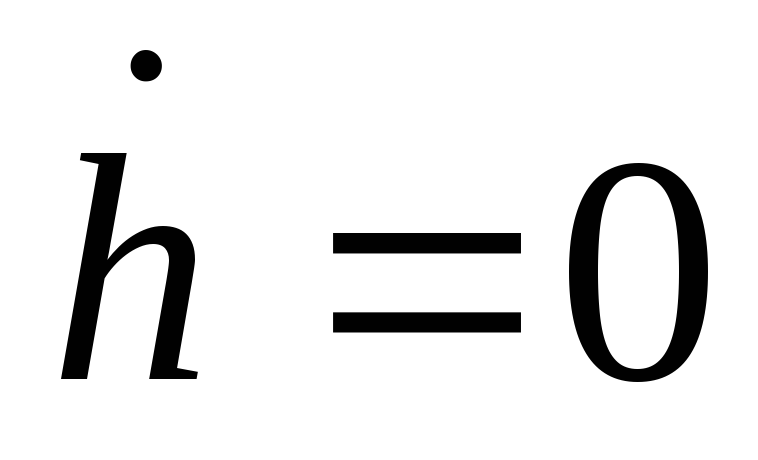 .
Покажите стрелками направления изменения
.
Покажите стрелками направления изменения
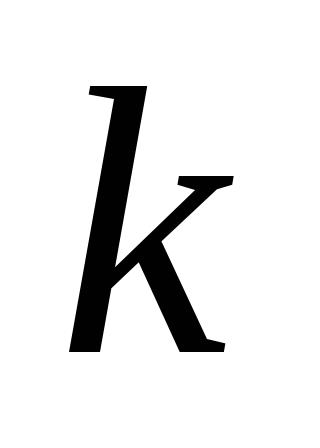 и
и
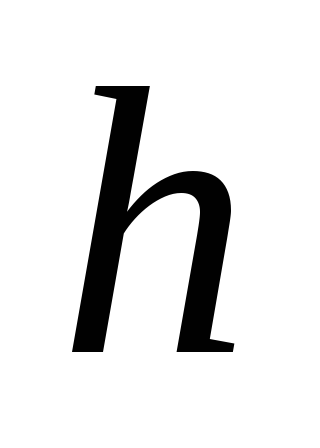 в каждой из четырех участков, на которые
разбивается плоскость линиями
в каждой из четырех участков, на которые
разбивается плоскость линиями
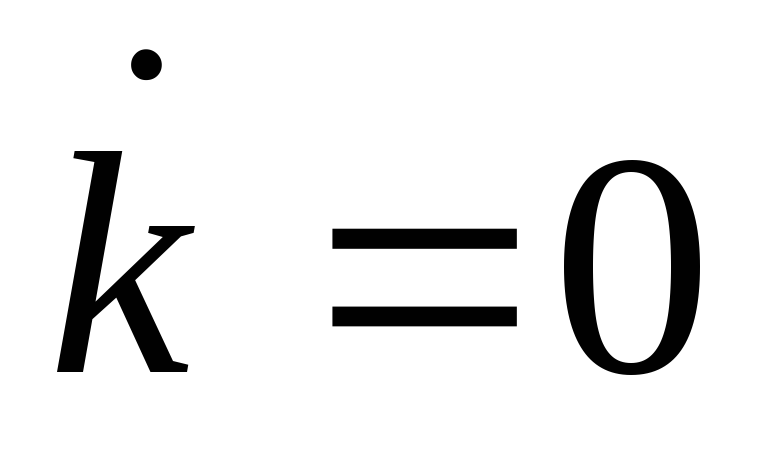 и
и
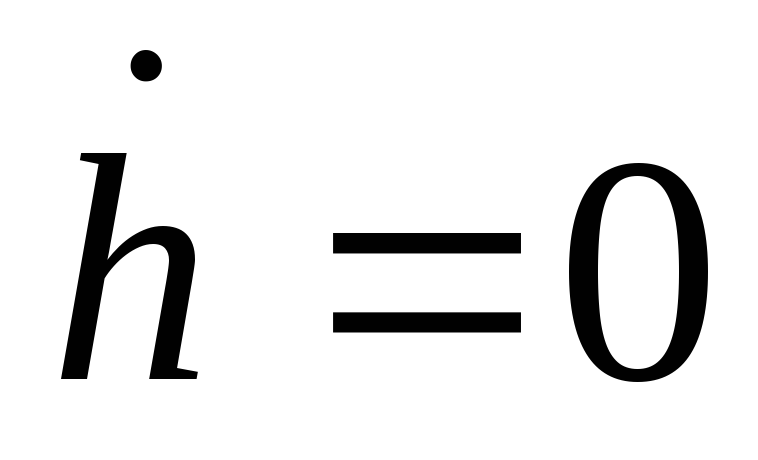 .
Изобразите несколько траекторий
динамики, которые бы показывали все
качественно различные случаи динамики
системы. Является ли траектория
сбалансированного роста локально
устойчивой?
.
Изобразите несколько траекторий
динамики, которые бы показывали все
качественно различные случаи динамики
системы. Является ли траектория
сбалансированного роста локально
устойчивой? -
Воспользуйтесь выражениями, задающими линии
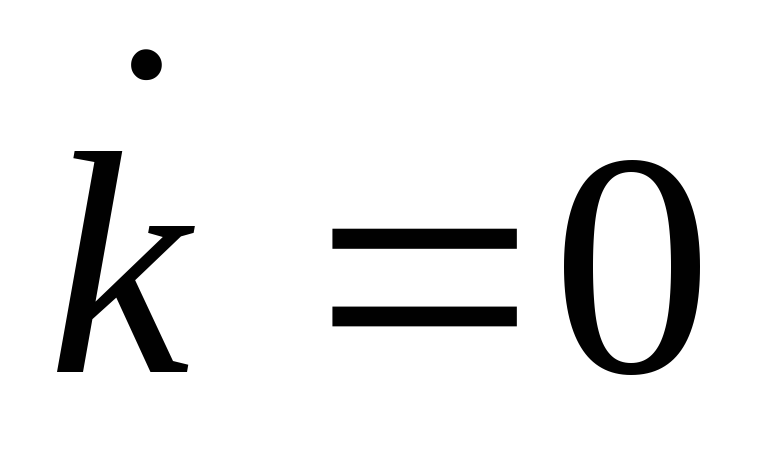 и
и
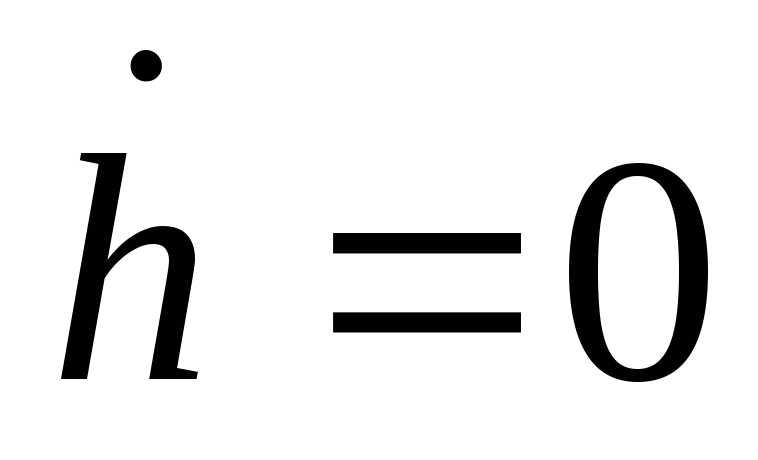 ,
и выведите из них логарифмы физического
и человеческого капитал на единицу
эффективного труда на траектории
сбалансированного роста (
,
и выведите из них логарифмы физического
и человеческого капитал на единицу
эффективного труда на траектории
сбалансированного роста (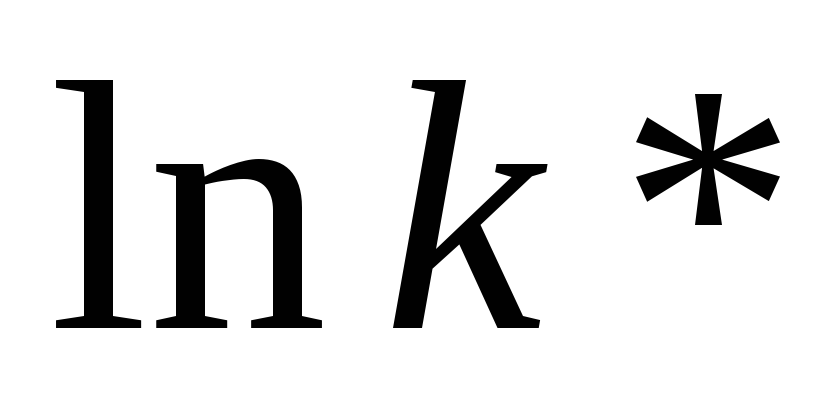 и
и
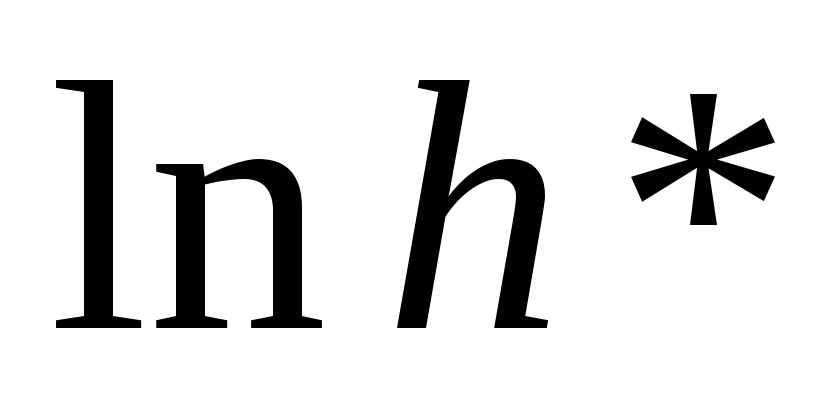 )
через параметры модели.
)
через параметры модели. -
Используя решение предыдущего задания, выразите выпуск на единицу эффективного труда на траектории сбалансированного роста (
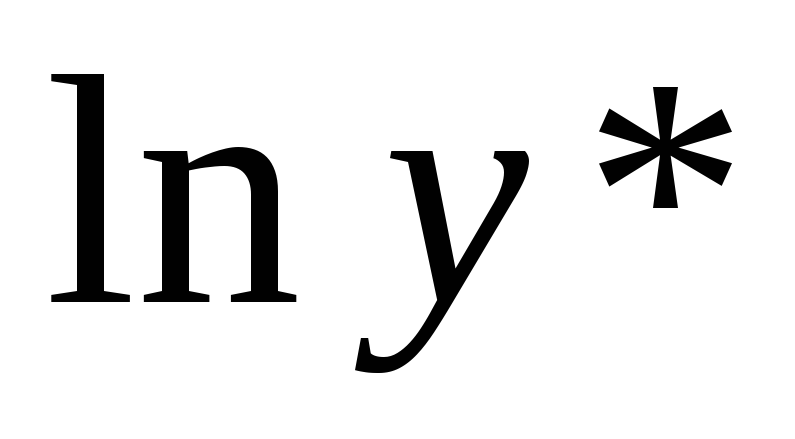 )
через параметры модели.
)
через параметры модели. -
Определите четыре следующих эластичности:
-
эластичности выпуска на единицу эффективного труда по норме сбережения в физический капитал;
-
эластичности выпуска на единицу эффективного труда по норме сбережения в человеческий капитал;
-
эластичности потребления на единицу эффективного труда по норме сбережения в физический капитал;
-
эластичности потребления на единицу эффективного труда по норме сбережения в человеческий капитал.
-
-
Определите нормы сбережений в человеческий и физический капитал, соответствующие золотому правилу.
-
Предположим, что экономика находится на траектории сбалансированного роста. Определите ставку процента и рыночную стоимость аренды единицы человеческого капитала в экономике, в которой запас капитала соответствует золотому правилу. Для этого в условия первого порядка фирм подставьте значения
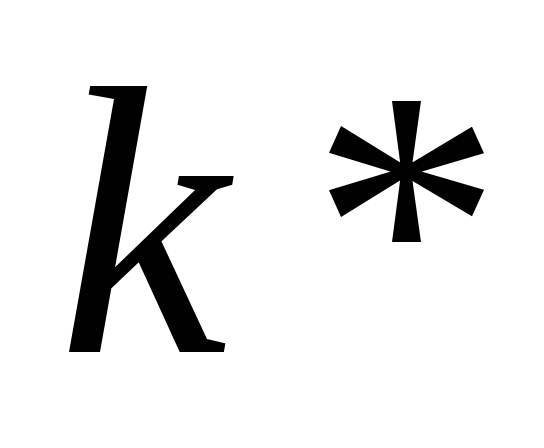 и
и
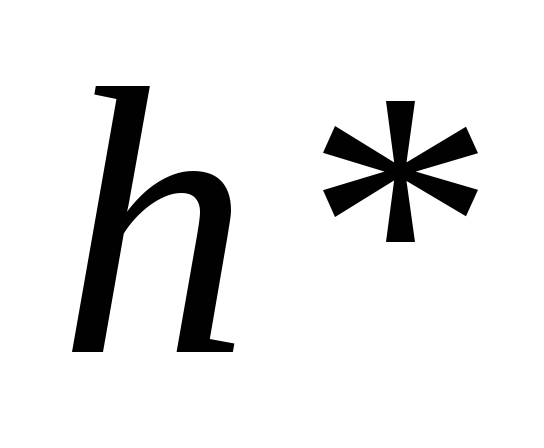 из задания 7, в которые вместо
из задания 7, в которые вместо
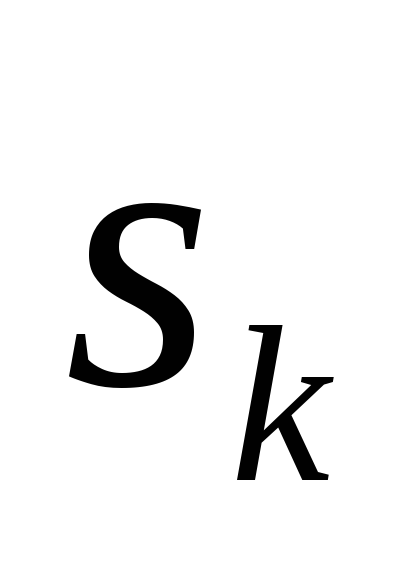 и
и
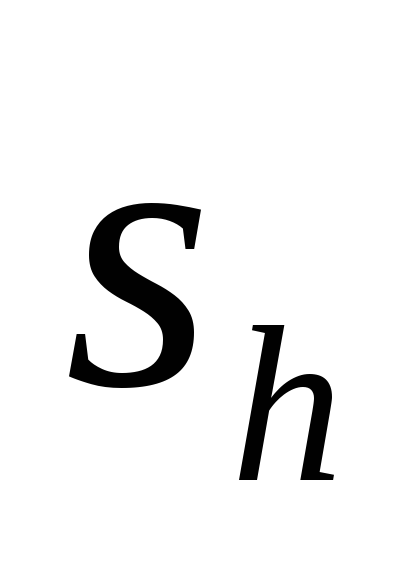 подставьте значения, найденные в задании
9. Как найденные ставка процента и
стоимость аренды капитала соотносятся
с темпами экономического роста на
траектории сбалансированного роста?
подставьте значения, найденные в задании
9. Как найденные ставка процента и
стоимость аренды капитала соотносятся
с темпами экономического роста на
траектории сбалансированного роста?
Решение.
1. Поделим производственную функцию
слева и справа на
![]() .
Получаем:
.
Получаем:
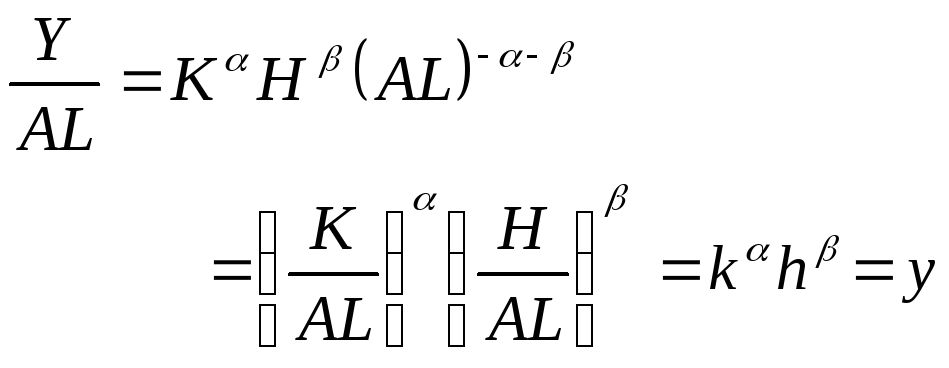
2. По определению
![]() ,
,
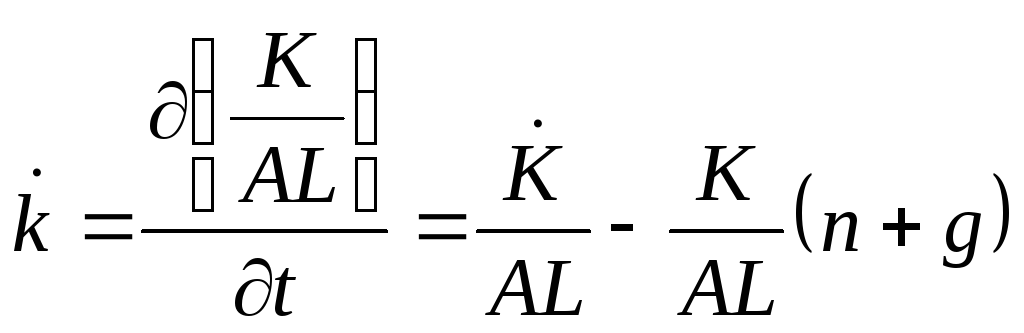
Подставляя
![]() ,
,
![]() и результат задания 1, получаем:
и результат задания 1, получаем:
(*)
![]()
Аналогично выводится выражение для
![]() :
:
(**)![]()
3. Из уравнения (*), имеем, что при
![]() ,
выполняется следующее выражение:
,
выполняется следующее выражение:
![]()
Из условия
![]() следует, что
следует, что
![]() .
Следовательно, линия
.
Следовательно, линия
![]() является выпуклой в системе координат
(k, h)
(см. рис.). Кроме того, из у
является выпуклой в системе координат
(k, h)
(см. рис.). Кроме того, из у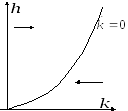 равнения
(*) мы видим, что если мы изначально
находимся на линии
равнения
(*) мы видим, что если мы изначально
находимся на линии
![]() ,
а затем увеличивается
,
а затем увеличивается
![]() без изменения
без изменения
![]() ,
то
,
то
![]() становится положительным. Следовательно,
становится положительным. Следовательно,
![]() возрастает везде выше линии
возрастает везде выше линии
![]() и сокращается везде ниже этой линии.
и сокращается везде ниже этой линии.
4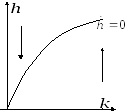 .
Из уравнения (*), имеем, что при
.
Из уравнения (*), имеем, что при
![]() ,
выполняется следующее выражение:
,
выполняется следующее выражение:
![]()
Из условия
![]() следует, что
следует, что
![]() .
Следовательно, линия
.
Следовательно, линия
![]() является вогнутой в системе координат
(k, h)
(см. рис. внизу). Кроме того, из уравнения
(**) мы видим, что если мы изначально
находимся на линии
является вогнутой в системе координат
(k, h)
(см. рис. внизу). Кроме того, из уравнения
(**) мы видим, что если мы изначально
находимся на линии
![]() ,
а затем увеличивается
,
а затем увеличивается
![]() без изменения
без изменения
![]() ,
то
,
то
![]() становится положительным. Следовательно,
становится положительным. Следовательно,
![]() возрастает
везде правее линии
возрастает
везде правее линии
![]() и сокращается везде левее.
и сокращается везде левее.
5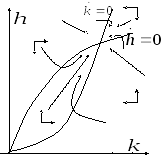 .
Совмещая рисунки, полученные в предыдущих
разделах, получаем следующую фазовую
плоскость для пары
.
Совмещая рисунки, полученные в предыдущих
разделах, получаем следующую фазовую
плоскость для пары
![]() и
и
![]() ,
изображенную на рисунке справа. Как мы
видим из рисунка, траектория
сбалансированного роста является
локально устойчивой.
,
изображенную на рисунке справа. Как мы
видим из рисунка, траектория
сбалансированного роста является
локально устойчивой.
6. Из заданий 3 и 4 следует следующая система уравнений, определяющая стационарное состояние:
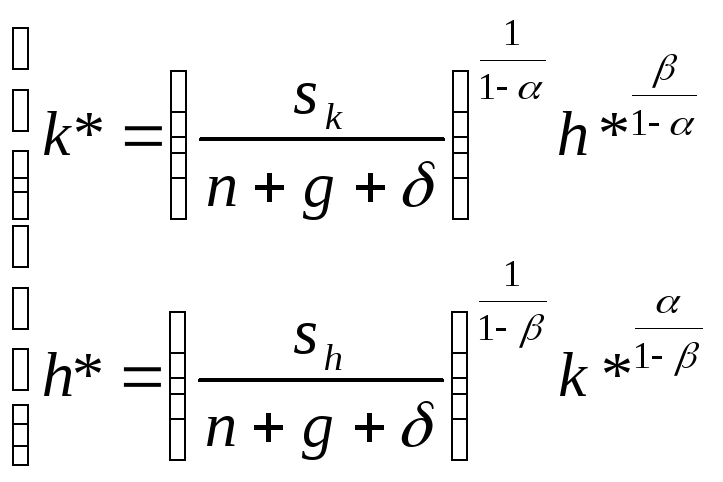
Прологарифмировав эти выражения,
получаем следующую линейную систему
уравнений относительно
![]() и
и
![]() :
:
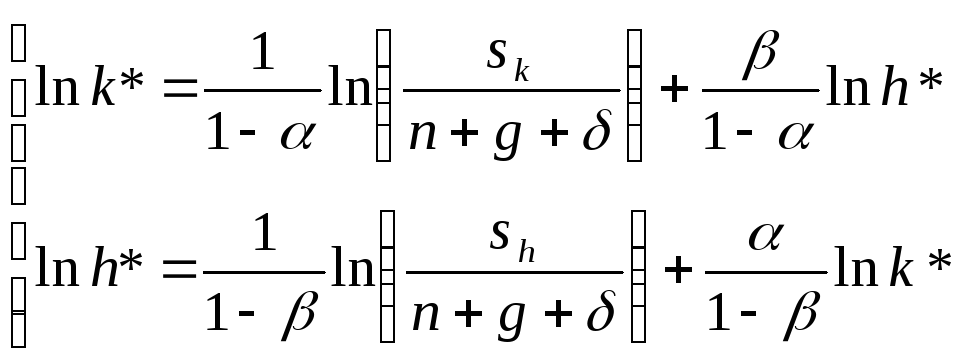
Откуда находим:
![]()
![]()
7. Используя предыдущее задание,
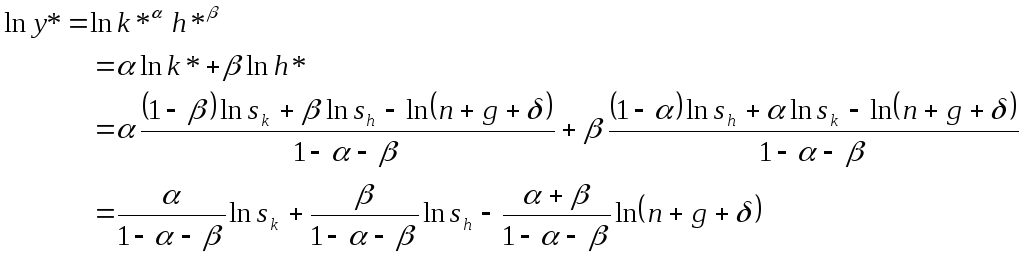
8. Эластичность выпуска на единицу
эффективного труда на траектории
сбалансированного роста по норме
сбережения в физический капитал равна
производной
![]() по
по
![]() :
:
![]()
Аналогичным образом находим
![]()
Зная, что
![]() ,
находим эластичность
,
находим эластичность
![]() по
по
![]() и
и
![]() :
:
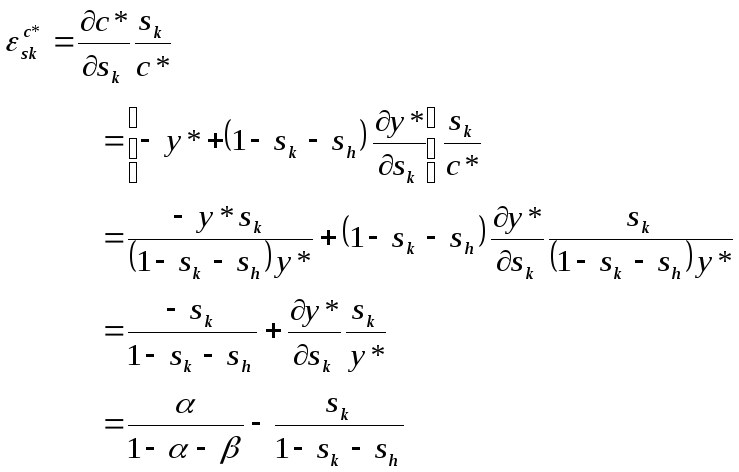
Аналогично
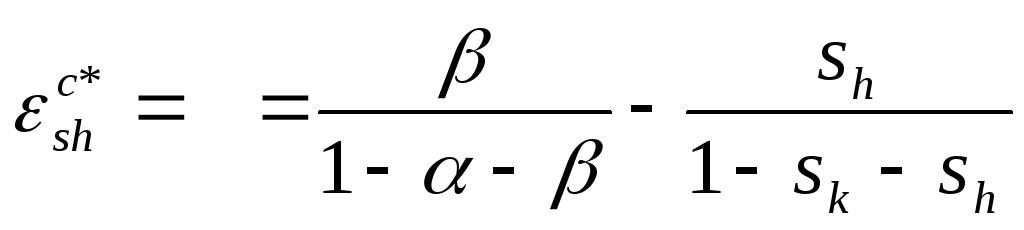
9. В точке максимума потребления
эластичности
![]() и
и
![]() должны быть равными нулю. Из предыдущего
задания мы видим, что это выполняется
в случае
должны быть равными нулю. Из предыдущего
задания мы видим, что это выполняется
в случае
![]() и
и
![]() .
.
10. Производя указанные операции, получаем:
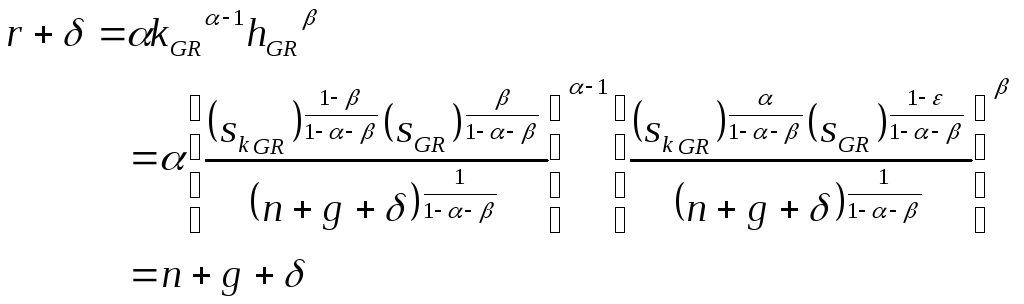
Откуда
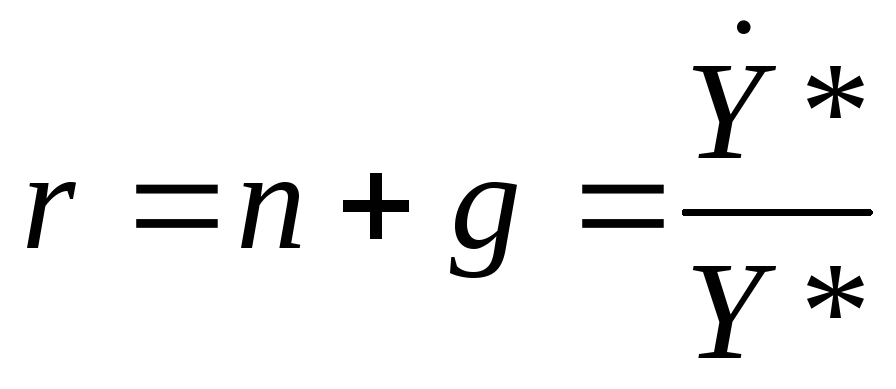
Аналогично находим