Макро Арефьев с хсехелп / Задачи на Солоу 2

Задача 1. Бухгалтерия роста.

Рассмотрим производственную функцию Кобба-Дугласа. Y = Kα Lβ , где Y - выпуск, K - капитал, L - труд, аα и β - параметры модели.

Задания:

1.Определите эластичность выпуска по капиталу и эластичность выпуска по труду.

2.На сколько процентов изменится выпуск, если капитал вырастет на 3%, труд сократится на 2%, при этом α = 13 , β = 14 .

3.Пусть y = lnY , k = ln K , и l = ln L . Запишите производственную функцию в

логарифмической форме. Другими словами, выразите y через k , l и параметры α и

β.

4.Найдите производные y по k и по l . Сравните результат с результатом первого задания и объясните значение фразы «Эластичность – это логарифмическая производная функции по её аргументам».

темп прироста рабочей силы. n ≡ L& . Сравните полученное выражение с

L

выражением, которое получается при взятии производственной от производственной функции в логарифмической форме по времени. Объясните понятие «логарифмическая производная по времени».

6.Определите отдачу от масштаба для данной производственной функции.

7.Предположим, что в экономике наблюдается совершенная конкуренция и невозрастающая отдача от масштаба. Определите долю дохода капитала, долю дохода труда и долю прибыли в общем доходе. Возможна ли в экономике совершенная конкуренция и возрастающая отдача от масштаба?

8.Предположим, что выпуск растет с постоянным темпом. Выразите выпуск Y в момент t через выпуск в нулевой момент времени Y0 , время t и темп прироста

выпуска gY . Выразите y через y0 , gY и t . Схематично изобразите графики функций Y(t) и y(t).

9.Предположим, что темп роста выпуска gY постоянен на интервале времени (0,t1 ) , затем плавно снижается до нуля на интервале (t1,t2 ) , в момент t2 мгновенно

достигает начального значения и более не изменяется. Изобразите графики функций gY (t), y(t),Y(t).

10.Предположим, что выпуск растет на 3% в год. За какое время выпуск вырастет в 2 раза? В 4 раза? В 10 раз?

11.Предположим, что в некоторой экономике (не обязательно согласующейся с заданием к данной задаче) доля дохода капитала в экономике составляет 13 , а доля дохода труда 23 . Капитал вырос за год на 4%, труд на 1%, а выпуск – на 3%. Можно ли эти данные объяснить с помощью производственной функции, используемой в данном задании? Чем может быть вызвано расхождение между исследуемой производственной функцией и реальной экономикой?

Задача 2. Вариации на тему теоремы Эйлера.

Рассмотрим производственную функцию Y = F(K, L), однородную степени γ :

F(λK,λL) = λγ F(K, L)

Задания.

1.Каков экономический смысл математического условия «однородность производственной функции степени γ »? Что вы можете сказать о случае γ = 1?

2.Докажите первую часть теоремы Эйлера. А именно, выведите соотношение

γF(K,L) = FK K + FL L .

Для этого продифференцируйте определение однородности степени γ по переменной λ и рассмотрите случай λ = 1.

3.Предположим, что в экономике наблюдается совершенная конкуренция. Выразите долю прибыли в выпуске через параметр однородности производственной функции

γ. Докажите, что в совершенно конкурентной экономике с постоянной отдачей от масштаба экономическая прибыль равна нулю. Докажите, что в экономике не может наблюдаться одновременно совершенная конкуренция и возрастающая отдача от масштаба.

4.Докажите вторую часть теоремы Эйлера. А именно, докажите, что если производственная функция имеет степень однородности γ , то предельный продукт труда и предельный продукт капитала однородны степени γ −1.

5.Предположим, что в экономике наблюдается совершенная конкуренция и невозрастающая отдача от масштаба. Сравните долю дохода труда и долю дохода капитала с эластичностями выпуска по труду и по капиталу.

6.Предположим, что в экономике наблюдается совершенная конкуренция и постоянная отдача от масштаба, при этом доля дохода труда в общем доходе составляет 23 . На сколько процентов вырастет выпуск, если труд вырастет на 2% , а капитал – на 5%.

Задача 3. По мотивам Basu, Fernald (1997). Returns to Scale in US. Production…. Journal of Political Economy 105(2): 249-283.

Рассмотрим производственную функцию вида Y = F(K, L, A). Предположим, что в экономике наблюдается несовершенная конкуренция, при этом спрос на продукцию одной фирмы имеет эластичность, равную (−σ ).

Введем следующие обозначения:

cK ,cL ,cM - доли расходов соответственно на капитал, на труд и на промежуточную продукцию в общих расходах;

sK ,sL ,sM ,sπ - доли доходов капитала, труда, промежуточной продукции и доля прибыли в общих доходах; γ - отдача от масштаба;

1.Покажите, что если производственная функция описывается постоянной отдачей от масштаба, в экономике наблюдается совершенная конкуренция, при этом технический прогресс нейтрален по Хиксу, то

d lnY = sK d ln K + sLd ln L + d ln A, где sK ,sL - доли доходов труда и капитала в общем доходе.

2.2. Выведите уравнение, связывающее между собой наценку фирм и эластичность спроса на продукцию одной фирмы. Выведите уравнение, связывающее между собой

отдачу от масштаба, наценку и долю прибыли в ВВП.

Подсказка 1: для определения размера наценки следует решить задачу

максимизации прибыли вида max P(Y )Y −TC(Y ), а для определения доли

Y

прибыли в ВВП – задачу вида max P(F (K, L))F (K,L)− (r +δ )K − wL .

K,L

Подсказка 2: будьте аккуратны с нормализацией цен. Нормализацию следует проводить после нахождения условий первого порядка задачи фирмы.

3.Базу и Фернальд оценивают долю прибыли в ВВП в 3%, а однородность производственной функции в 101%. Каков средний размер наценки?

4.Пусть технология производства одной фирмой задается уравнением

Y = F(K, L,M, A) , где М – промежуточная продукция. Покажите, что в случае нейтральности по Хиксу технического прогресса, несовершенной конкуренции и непостоянной отдачи от масштаба, мы можем записать:

d lnY = γ [cLd ln L + cK d ln K + (1− cL − cK )d ln M ]+ d ln A , где cL ,cK - доли расходов на труд и на капитал в общих расходах.

5.Покажите, как связаны между собой доли доходов sK ,sL ,sM ,sπ и доли расходов cK ,cL ,cM .

6.Покажите, как связаны между собой прирост выпуска, и прирост добавленной стоимости одной фирмы? (ответ: dv = (dy − sM )dm(1− sM ) ). При какой технологии

прирост выпуска всегда равен приросту добавленной стоимости?

Задача 4. Экономика Робинзона.

Робинзон на необитаемом острове выращивает кокосы. Кокосовые пальмы требуют определенного ухода, поэтому количество выращенных кокосов нелинейно зависит от

количества посаженных кокосов: Yˆ = 1000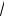LK , где K - количество посаженных кокосов,

Yˆ - количество выращенных кокосов, а L - количество работников, L = 1. Часть кокосов (20% от количества выращенных кокосов) воруют дикие обезьяны, таким образом,

Робинзону достается лишь Y = 0,8Yˆ кокосов. Робинзон каждый год съедает половину доставшихся ему кокосов, C = 12 Y а оставшиеся кокосы сажает, чтобы получить урожай в

следующем году. Посаженый кокос дает урожай только один раз, через год. Задание

1.Определите зависимость количества посаженных кокосов в текущем году Kt от количества посаженных кокосов в предыдущем году Kt−1 .

2.Постройте диаграмму Kt (Kt−1 ). Определите точку, в которой Kt = Kt−1 ≡ K *. Найдите значение K *, Y * и C *

3.Растет или сокращается K , если Kt < K *? Если Kt > K *?

4.Предположим, что изначально K0 = K *. Покажите, какая будет динамика K , Y и

C , если Робинзон сможет улучшить технологию выращивания кокосов до

Yˆ = 2250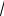KL . Как изменится выпуск в год, когда произошла инновация, а также выпуск, соответствующий стационарному состоянию K = K *? В обоих случаях определите, какая доля изменения выпуска произошла за счет изменения количества посаженных кокосов, а какая – за счет изменения остатка Солоу.

5.Предположим, что Робинзон нашел себе 15 помощников – Пятниц, так что теперь кокосы начали выращивать 16 человек. Какая будет динамика K , Y и C , а также

K , Y и C ? Как изменится общий выпуск и выпуск на одного работника в год,

L L L

когда произошло изменение численности, а также общий выпуск и выпуск на одного работника, соответствующие стационарному состоянию K = K *? В обоих случаях определите, какая доля изменения общего выпуска произошла за счет изменения количества посаженных кокосов, какая за счет изменения количества занятых, и какая за счет изменения остатка Солоу.

6.Домашнее задание: решите пункты со 2 по 5 численно в электронных таблицах (например, в Excel).