
Макро Арефьев с хсехелп / Basic_Solution_var2
.pdf
Контрольная работа по макроэкономике. Блок “Теория экономического роста”.
Задание 1. Рассмотрите модель Солоу с |
производственной функцией Y K (AL)1 , |
||||
динамика технологии и рабочей силы |
A |
g, |
L |
n . Правило накопления капитала |
|
A |
L |
||||
|
|
|
|||
K sY K .
Пусть изначально экономика находится на траектории сбалансированного роста, при этом 1/ 3, s 1/ 4, n g 0,06, 0,03 . В момент времени t происходит дискретное
сокращение нормы сбережений до 0,16. Определить значение темпа прироста ВВП сразу после данного изменения.
Решение 1.1. Изначально экономика находится на траектории сбалансированного роста, где
( |
|
) |
|||||||
откуда |
|
||||||||
|
|
|
|
|
|
|
|
|
|
1.2 Из основного уравнения динамики модели Солоу |
|||||||||
|
|
|
|
̇ |
|
||||
|
|
|
|
( |
) |
||||
|
|
||||||||
откуда можем найти изменение темпов прироста капиталовооруженности в момент шока:
̇
( )
Ввиду того, что до шока экономика находилась на траектории сбалансированного роста и темп прироста капиталовооруженности эффективного труда равнялся нулю, сразу после шока темп прироста капиталовооруженности эффективного труда составит годовых.
1.3. Из производственной функции в интенсивной форме получаем:
̇̇
1.4 По определению производительности эффективного труда |
, откуда |
̇̇ ̇ ̇
Таким образом, сразу после шока выпуск будет расти с темпом |
в год. |
||||
Задание 2. Рассмотрите модель Солоу с производственной |
функцией Y K (AL)1 , |
||||
динамика технологии и рабочей силы |
A |
g, |
L |
n . Правило накопления капитала |
|
|
|
||||
|
A |
L |
|
||
K sY K .
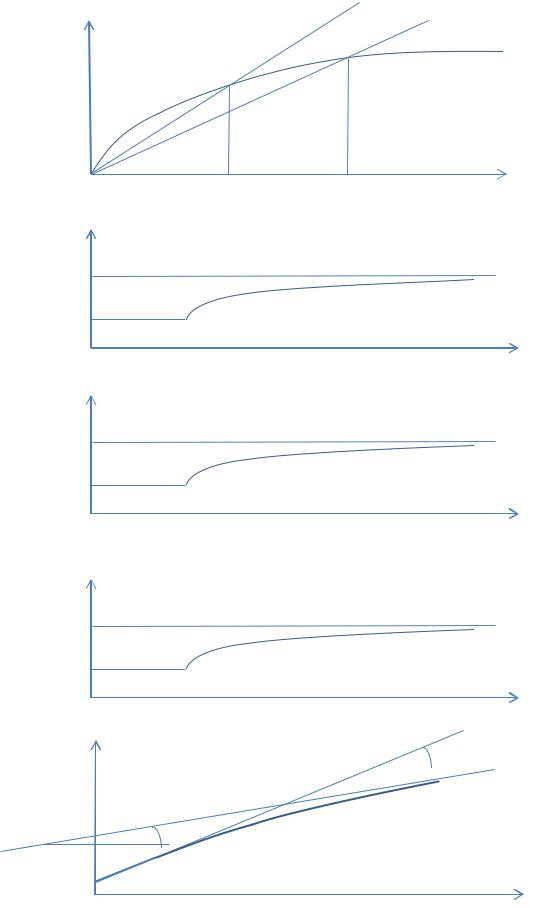
Покажите на диаграмме Солоу, как повлияет на равновесие снижение темпов прироста параметра технического прогресса. Покажите, какая будет динамика капиталовооруженности эффективного труда, производительности эффективного труда, потребления на единицу эффективного труда, логарифма выпуска, логарифма капитала, логарифма потребления на душу населения, темпа прироста выпуска и ставки процента. Поясните выполненные построения.
Решение |
|
|
|
|
|
2.1 Диаграмма Солоу |
( |
) |
( 1 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
1
2.2 Капиталовооруженность эффективного труда
1
2.3 Производительность эффективного труда
1
2.4 Потребление на единицу эффективного труда
1
2.5 Логарифм выпуска
ln |
|
|
|
|
|
|
1
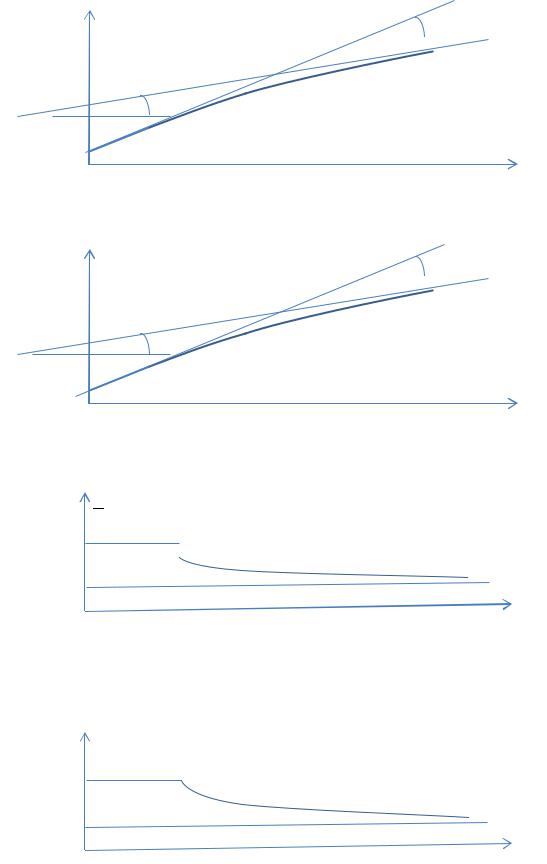
2.6 Логарифм капитала
ln |
|
|
|
|
|
|
1
2.7 Логарифм потребления на душу населения
ln |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|||
2.8, 2.9 Темп прироста выпуска
̇
|
1 |
|
Оценивание: п. 2.8 относится к общей форме графика (все кроме скачка в момент шока), п. 2.9 засчитывается в случае, если указан скачок. Если пункт 2.8 не засчитан, то пункт 2.9 также не засчитывается.
2.10 Ставка процента
1

Задание 3. Предположим, что две экономики описываются моделью Солоу с производственной функцией Y K (AL)1 , где Y - выпуск, K - капитал, A - параметр
эффективности труда, L - труд, - параметр модели.. Доля дохода капитала в общем доходе в обеих экономиках составляет 1/2, темп прироста численности населения равен 2% в год, темп прироста параметра эффективности труда составляет 1,5% в год, а норма амортизации составляет 2,5% в год. Обе экономики находятся на траектории сбалансированного роста, при этом потребление на душу населения различается между ними в 3 раза.
а) Предположим, что потребление на душу населения различается лишь за счет нормы сбережений, при этом в первой (более богатой) стране норма сбережения составляет 1/4. Определите, какой должна быть норма сбережения во второй стране.
б) Предположим, что нормы сбережения одинаковы и равны 1/4, а потребление на душу населения различается лишь за счет различий в параметре эффективного труда. Определите, во сколько раз должны различаться значения параметра эффективности труда.
Решение Задание 3а) Допускаются два варианта решения
Вариант решения 1 (точные вычисления): 3.1 На ТСР имеем:
( |
|
) ( |
|
|
|
|
|
) |
1 |
||||||
|
|
|
|
|
|
||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
1 |
( |
1 |
) |
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
√
Вариант решения 2 (приближенные вычисления):
3.2 Эластичность потребления по норме сбережений составляет
Если потребление различается на 200%, то норма сбережений должна различаться на
|
, т.е. в 4 раза. Получаем: |
|
⁄ |
||
|
Задание 2б)
3.3 На траектории сбалансированного роста экономики будут стремиться к одному
значению потребления на единицу эффективного труда 1 |
, откуда получаем: |
|||||||||
1 |
1 |
1 |
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Следовательно, значение параметра эффективности труда должно различаться в 3 раза.
Задание 4. Вопросы по статье “ N. Gregory Mankiw, David Romer, David N. Weil. A Contribution to the Empirics of Economic Growth. Quarterly Journal of Economics, Volume 107, issue 2 (May, 1992), 407-437.”
а) Выведите уравнение из модели Солоу, дополненной человеческим капиталом, которое авторы статьи тестируют в своей работе, и которое определяет различия в доходах между странами.
ln |
Y t |
ln A 0 gt |
|
ln s |
|
|
|
|
ln n g |
|
ln(s |
|
) |
||
|
|
|
1 |
k |
|
|
1 |
h |
|||||||
|
|
|
|
1 |
|
|
|
||||||||
|
L t |
|
|
|
|
|
|
|
|||||||
Чему будет равна в данном случае эластичность выпуска на душу населения по норме сбережений в физический капитал, если доля дохода капитала в выпуске равна
эластичности выпуска по физическому капиталу и составляет 1/3? Ответ обоснуйте, указав все используемые Вами предпосылки.
б) Почему исключение из анализа человеческого капитала приводит к завышению роли физического капитала?
4.1…4.9 Вывод уравнения 4.1 Предпосылки модели:
( )1
̇
̇
4.2 Из данных предпосылок выводятся уравнения динамики в интенсивной форме:
̇ |
( |
) |
|
|||
̇ |
( |
) |
|
|||
4.3 На траектории сбалансированного роста |
̇ , и ̇ откуда |
|||||
1 |
1 |
|
|
|
|
|
4.4 Решив данную систему уравнений, получаем: |
||||||
|
1 |
|
1 |
|
||
|
1 |
|
||||
|
( |
|
|
) |
|
|
|
|
|
||||
|
1 |
|
1 |
|
||
|
1 |
|
||||
|
( |
|
|
) |
|
|
|
|
|
|
|
||
4.5 Подставив полученные уравнения в производственную функцию в интенсивной форме, имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
( |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|||
|
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
||||||
4.6 |
По определению производительности эффективного труда, |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|||
|
|
|
|
( |
|
) |
|
|
|
|
|
|
||||||||
4.7 |
Прологарифмировав данное выражение, имеем: |
|
|
|
|
|
|
|
||||||||||||
ln ( |
|
) ln |
|
|
|
ln |
|
|
ln |
|
|
|
|
|
ln( |
) |
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
4.8 |
Эластичность является логарифмической производной, следовательно, эластичность |
||||||||||
подушевого выпуска по норме сбережений составит |
|
||||||||||
|
|
|
|
(ln ( |
|
)) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ln |
) |
|
|
|
|
|
4.9 |
По условию задачи |
1 |
. В литературе существуют различные оценки значения |
||||||||
|
|||||||||||
параметра ; Mankiw, Romer and Weil дают оценку |
. В этом случае эластичность |
||||||||||
подушевого выпуска по норме сбережений в физический капитал составит: |
|||||||||||
|
|
|
|
|
|
|
⁄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
⁄ |
|
⁄ |
|
||
4.10, 4.11 В статье обсуждаются следующие причины, по которым роль физического капитала в модели Солоу без человеческого капитала оказывается переоцененной:

4.10 В модели с человеческим капиталом коэффициент перед ln при заданных значениях и оказывается больше, чем в модели без человеческого капитала
Поэтому при одинаковом значении коэффициента при ln модель без человеческого капитала предполагает большее значение параметра .
4.11 Ввиду того, что норма сбережения в человеческий капитал положительно коррелирует с нормой сбережения в физический капитал, исключение из регрессии ln приведет к смещенной (завышенной) оценке коэффициента перед ln .
Задание 5. Вопросы по статье “Arnold C. Harberger. A Vision of the Growth Process. The American Economic Review, Vol. 88, No. 1 (Mar., 1998), pp. 1-32”
а) По данным, представленным в таблице, постройте солнечную диаграмму:
Отрасль |
Начальное |
Прирост общей |
|
значение |
производительности |
|
добавленной |
факторов |
|
стоимости |
|
1 |
500 |
-20% |
2 |
1000 |
+30% |
3 |
1500 |
+10 |
4 |
2000 |
-10 |
5.1…5.5 Предварительные расчеты
|
|
Снижение |
|
|
|
|
|
реальных |
|
Начальное |
|
|
Прирост совокупной |
затрат в |
|
значение |
|
|
производительности |
абсолютном |
Кумулятивная |
добавленной |
Кумулятивная |
Отрасль |
факторов, % |
выражении |
сумма (5.3) |
стоимости |
сумма (5.1) |
№ |
5.2 |
5.3 |
5.4 |
5.1 |
5.5 |
1 |
30% |
300 |
300 |
1000 |
1000 |
2 |
10% |
150 |
450 |
1500 |
2500 |
3 |
-10% |
-200 |
250 |
2000 |
4500 |
4 |
-20% |
-100 |
150 |
500 |
5000 |
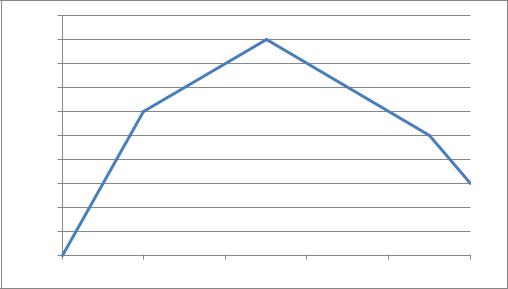
5.6, 5.7 Координаты солнечной диаграммы
п. 5.6 п. 5.7
0,00% 0,00%
20,00% 6,00%
50,00% 9,00%
90,00% 5,00%
100,00% 3,00%
5.8 Солнечная диаграмма
10,00% |
|
|
|
|
|
|
9,00% |
|
|
|
9,00% |
|
|
8,00% |
|
|
|
|
|
|
7,00% |
|
|
|
|
|
|
6,00% |
|
6,00% |
|
|
|
|
5,00% |
|
|
|
|
|
5,00% |
4,00% |
|
|
|
|
|
|
3,00% |
|
|
|
|
|
3,00% |
2,00% |
|
|
|
|
|
|
1,00% |
|
|
|
|
|
|
0,00% |
0,00% |
|
|
|
|
|
0,00% |
20,00% |
40,00% |
60,00% |
80,00% |
100,00% |
|
б) Что означают термины «дрожжевой рост» и «грибной рост»? Решение:
5.9Дрожжевой рост – экономика растет приблизительно равномерно во всех отраслях.
5.10Грибной рост – рост возникает лишь в небольшой доле отраслей
5.11При грибном росте отрасли, которые в одном периоде являются лидерами, вряд ли сохранят лидерство в следующем периоде
