Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «Высшая школа экономики»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

СЭКС хсехелп / Все формулы ТСН

.doc

Скачиваний:

Добавлен:

02.06.2015

Размер:

270.85 Кб

Скачать

☆

I. Характеристика индивидуальных свойств совокупности

II. Средняя

Средняя арифметическая	Абсолютный	Используется в случае наличия n простых элементов
Средняя степенная	Абсолютный	Используется при k = 2 для расчета средней при необходимости избавиться от знака
Средняя геометрическая	Соответствует типу y	Используется в случае, если общий объем средней получается умножением вариантов (e.g. коэффициентов роста). При этом считается средняя за период. Если период делится на m подпериодов и интересует средняя подпериодная
Средняя гармоническая	Абсолютный	Используется, если при x взвешивании используются значения x, стоящего в числителе усредняемой относительной величины

III. Распределение

Плотность		Относительный
Доля элементов, значение признака которых меньше определенного значения		Относительный
Доля / частость / удельный вес		Относительный
Показатель нагрузки		Относительный
Коэффициент координации		Относительный

IV. Центральное значение

Мода		Абсолютный	- для равных интервалов
Мода		Абсолютный	- для возрастающих интервалов

V. Порядковые статистики

Медиана

Абсолютный

Вид средней, при этом 50% признаков меньше Ме, 50% больше Ме.

Квартиль уровня k

Абсолютный

Квартили делят совокупность на 4 части.

Q₀ = x_min; Q₃ = Me; Q₅ = x_max.

Дециль уровня k

Абсолютный

Децили делят совокупность на 10 частей.

D₀ = x_min; D₅ = Me; D₁₀ = x_max.

VI. Оценка формы распределения

Коэффициент асимметрии по Пирсону	Относительный	Вершина распределения смещена влево. Вершина распределения смещена вправо.
Коэффициент асимметрии по Линдбергу	Относительный
Коэффициент эксцесса по Пирсону	Относительный	Распределение остроконечно. Распределение плоскоконечно.
Коэффициент эксцесса по Линдбергу	Относительный	Распределение остроконечно. Распределение плоскоконечно.

VII. Дифференциация и концентрация

Коэффициент Герфиндаля	Абсолютный
Половинный квартильный размах	Относительный	Показывает изменчивость по центральным 50% элементов совокупности.
Коэффициент Джини	Относительный
Квартильный коэффициент	Относительный
Децильный коэффициент	Относительный

VIII. Оценка вариации

Стандартная ошибка	Абсолютный	Среднее отклонение
Дисперсия	Относительный	Мера рассеивания
Мера отклонения от величины A	Относительный
Стандартная ошибка отклонения от величины A	Абсолютный
Коэффициент вариации	Относительный	Отражает степень неравномерности совокупности низкая неравномерность умеренная неравномерность высокая неравномерность
Коэффициент изменчивости категорий (индекс качественной вариации)	Относительный	Измеряет, какую часть составляет наблюдаемая изменчивость категорий при заданных количествах наблюдений и групп.

IX. Оценка структурных различий

Коэффициент Казинца		Абсолютный	Показывает, насколько в среднем различается вклад групп.
Индекс Гатева		Относительный	Характеризует относительную значимость различий двух структур. Используются, если различия происходят без различия в доминировании.
Индекс Салаи		Относительный
Коэффициент неравномерности		Относительный	L – максимальное количество групп, входящих в доминантную.
Правило сложения дисперсий	,		n_i – число единиц в i-той группе
Эмпирический коэффициент детерминации		Относительный	Измеряет долю общей (суммарной) дисперсии целеевого признака, объясняемого влиянием группировочного признака.
Эмпирический коэффициент корреляции по Пирсону		Относительный

X. Оценка тесноты и сопряженности

Коэффициент квадратичной взаимосопряженности	Относительный
Коэффициент взаимосопряженности Пирсона	Относительный
Коэффициент взаимосопряженности Чупрова	Относительный	Не рассчитывается для таблицы «четырех полей»
Коэффициент пропорционального уменьшения ошибки	Относительны
Коэффициент ассоциации Юла	Относительный	Для таблиц «четырех полей» вида
Коэффициент контингенции Пирсона	Относительный	Для таблиц «четырех полей» вида

Анализ совокупности с течением времени

Абсолютный прирост	Абсолютный	Показывает, насколько значение признака в периоде i + 1 отличается от значения в периоде i (0).
Коэффициент роста	Относительный	Показывает, во сколько раз значение признака в периоде i + 1 отличается от значения в периоде i (0).
Темп роста	Относительный
Темп прироста	Относительный
Абсолютное значение 1% прироста
Средний абсолютный прирост	Абсолютный
Средний коэффициент роста	Относительный
Средний темп роста	Относительный
Средний темп прироста	Относительный
Коэффициент опережения	Относительный	Показывает, во сколько раз одна величина растет быстрее другой.
Средний уровень ряда	Абсолютный	- в ряду динамики в интервальном ряду абсолютных величин и в ряду средних величин.
	Абсолютный	- в моментном ряду с равностоящими уровнями.
	Абсолютный	- в моментном ряду с неравными промежутками
Относительный показатель плана	Относительный
Относительный показатель выполнения	Относительный
Относительный показатель динамики	Относительный

Построение тренда. Прогнозирование

Если совокупность по каждому году однородна, т.е. V < 33% для каждого года, то тогда значение признака осредняется с помощью средней арифметической. (с) Поповская Е.В.
Если V > 33% и имеются данные более, чем по трем годам, используется метод скользящей средней, причем длина интервала осреднения равна количеству периодов, на который делится год.
Строится ряд скользящей средней.
Находится отношение фактического значения признака к значению скользящей.
Находятся средние: арифметическая, модальная, модифицированная — для полученных в п.4 соотношений для каждого квартала по всем годам.

где — ряд без .

Выбирается та форма средней, сумма по периодам (кварталам, месяцам) ближе всего к их количеству (N: 4; 12). Про остальные средние можно забыть.
Находится поправочный коэффициент как отношение количества периодов к сумме средних. .
Контроль: .
Находятся индексы сезонности: для r-го периода: .
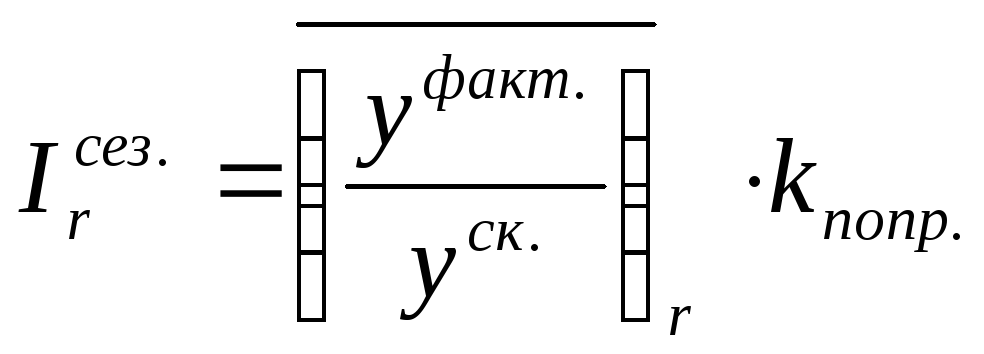Строится выровненный ряд: .
Построение линейного тренда
В центр ряда (т.е. на уровне элемента под номером ⁿ/₂) ставится нулевой момент времени: t = 0. В соответствии с этой шкалой каждому уровню присваивается свой момент времени.
Уравнение прямой: y = a + bt. .
Согласно формуле в п. 14, рассчитываются теоретические (расчетные) уровни — тренд.
Рассчитывается формула Тейла (?): 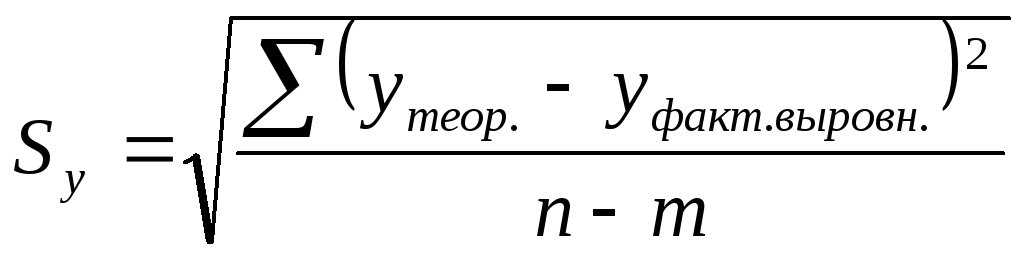, где n — кол-во уровней, m — кол-во неизвестных в уравнении тренда: (для прямой m = 2 — это a и b).
Рассчитывается показатель формулы Тейла (?):. V < 0,33 можно прогнозировать на 20% длины динамического ряда; V < 0,67 можно прогнозировать на 10% длины динамического ряда.
Находится прогнозируемое значение признака:
Интервальная оценка: , где t — что-то там, значение спросить у препода.

Соседние файлы в папке СЭКС хсехелп

#
02.06.2015463.12 Кб15Вариант 5.jpg
#
02.06.2015416.32 Кб16Вариант 6.jpg
#
02.06.2015431.89 Кб16Вариант 7.jpg
#
02.06.2015998.02 Кб16Вариант 8.jpg
#
02.06.20151.29 Mб15Вариант 9.jpg
#
02.06.2015270.85 Кб29Все формулы ТСН.doc
#
02.06.2015274.55 Кб18дз тсн мясо и мясопродукты
#
02.06.2015283.13 Кб16дз тсн овощи и бахчевые
#
02.06.2015277.5 Кб28ДОПОЛНЕННЫЕ все формулы ТСН.doc
#
02.06.201544.85 Кб18пояснительная записка
#
02.06.201539.99 Кб19распечатка 2 этап.xlsx