Лекция №4 Тема 2. Задача нелинейного программирования (продолжение)

2. Задачи выпуклого программирования

   1. Выпуклые множества

2.1.1. Понятие выпуклого множества

Определение. МножествоSEⁿназывается выпуклым, если для любых двух точек и имеем

при любом . Геометрически это означает, что вместе с и и весь отрезок принадлежит множеству . Отметим, что отрезок называется выпуклой комбинацией точек и .

Примеры выпуклых множеств

1. Eⁿ.

2. Пустое множество.

3. Множество, состоящее из одной точки

,

где .

4. Гиперплоскость

,

где , a ≠0, иb– число. Приn = 3 это множество совпадает с обычной плоскостью, а приn = 2 – с прямой.

5. Полупространство

,

где , a ≠0, иb– число.

6. Конус

,

а y^(k)– заданные векторы . Заметим, что часто рассматриваются конусы с вершиной не в нуле, а в какой-либо другой точке , то есть множества типа

7. Выпуклая комбинация (оболочка) конечного числа точек

.

Такое множество геометрически представляет собой n-мерный выпуклый многогранник.

8. Пересечение конечного числа полупространств

,

где.Такое множество называется многогранным выпуклым множеством. В том случае, когда оно ограничено, оно также является выпуклым многогранником. Таким образом, возможны два представления выпуклого многогранника – в виде выпуклой оболочки конечной совокупности точек и в виде пересечения конечного числа полупространств, заданных неравенствами.

9. Шар радиуса r≥0 с центром в

.

В качестве примеров невыпуклых множеств можно назвать множество целых чисел или множество рациональных чисел.

2.1.2. Свойства выпуклых множеств

1. Пересечение любого числа выпуклых множеств является выпуклым множеством.

2. Объединение двух выпуклых множеств не обязательно выпукло.

Пример:объединение двух точек не есть выпуклое множество.

3. Геометрическая сумма , двух выпуклых множеств и, определяемая как

,

также является выпуклым множеством.

4. Произведение выпуклого множества на числоα, определяемое как

также является выпуклым множеством.

Эти утверждения следуют из определения выпуклого множества. Докажем,например, первое утверждение для пересечения двух множеств и. Пусть. Рассмотрим

.

Из выпуклости A иBполучаем, что и при всех .Отсюда. Утверждение доказано.

Определение.Крайней (экстремальной) точкойвыпуклого множества называется такая его точка, которая не может быть представлена в виде выпуклой комбинации двух различных точек этого множества.

В качестве примера приведем выпуклый многогранник. Его крайними точками являются его вершины.

Определение. МножествоSEⁿназываетсястрого выпуклым, если оно выпукло и все его граничные точки являются крайними.

Примером строго выпуклого множества является замкнутый шар.

2.1.3. Опорная гиперплоскость

Рассмотрим важнейшее понятие опорной гиперплоскости. Прежде всего заметим, что любая гиперплоскость , где , a ≠0, определяет в пространстве два замкнутых полупространства

и .

Гиперплоскость является пересечением этих полупространств и одновременно границей каждого из них.

Пусть имеется некоторое выпуклое множество Sи его граничная точкаy.

Определение. ГиперплоскостьH, проходящая через точкуyи содержащая все точки множествоSв одном из определяемых ею замкнутых полупространств, называется гиперплоскостью,опорной к множествуSв точкеy.

Можно показать, что опорную гиперплоскость можно провести через любую граничную точку выпуклого множества. Иллюстрация опорной гиперплоскости приведена на рис. 3.1.

Рис. 3.1. Опорная гиперплоскость H к выпуклому множеству S в точке y.

Отметим, что опорная гиперплоскость может быть не единственна (см. рис. 3.2).

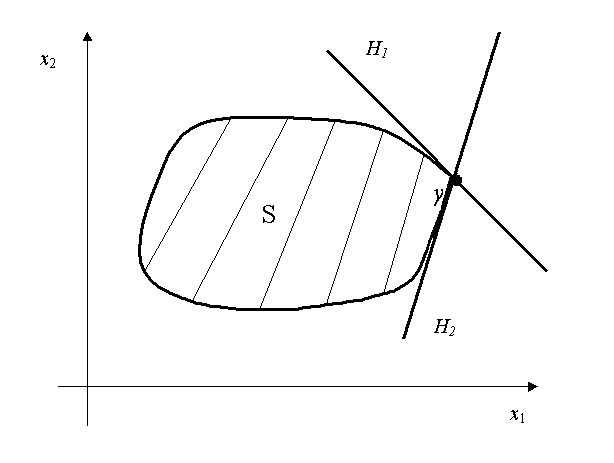
Рис. 3.2. Две опорных гиперплоскости H₁ и H₂ к выпуклому множеству S в точке y.

Пусть теперь задано два непустых множества AиB. ГиперплоскостьHназываетсяразделяющей гиперплоскостью, если все точки множестваAлежат в одном из замкнутых полупространств, определяемых гиперплоскостьюH, а все точки множестваBлежат в другом из определяемых ею замкнутых полупространств. Можно доказать несколько теорем о разделяющих гиперплоскостях. Рассмотрим простейшую из них. Пусть– совокупность внутренних точек множестваA.

Теорема 3.1. ПустьAиB– два непустых выпуклых множества, причемØ. Тогда существует гиперплоскостьH, разделяющая множестваAиB. ¹

Примеры разделяющих гиперплоскостей приведены на рис. 3.3 и 3.4.

Рис. 3.3. Гиперплоскость H разделяет множества S₁ и S₂, не имеющие общую точку

Рис. 3.4. Гиперплоскость H разделяет множества S₁ и S₂, имеющие общую точку

2. Выпуклые и вогнутые функции