
- •Сапіліді т.М., Демчик с.П. Математичний аналіз
- •Криволінійні інтеграли Криволінійний інтеграл першого роду
- •Криволінійний інтеграл другого роду
- •Зв’язок між криволінійними інтегралами:
- •Умови незалежності криволінійного інтегралу від шляху інтегрування:
- •Поверхневі інтеграли
- •Застосування поверхневих інтегралів першого роду
- •Поверхневий інтеграл другого роду.
- •Зв’язок між потрійними та поверхневими інтегралами. Формула Остроградського-Гауса
- •Зв’язок між криволінійним та поверхневим інтегралами. Формула Стокса
- •Теорія поля
- •Типові завдання
- •Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Сапіліді т.М., Демчик с.П., 2015р. Зміст
Зв’язок між криволінійним та поверхневим інтегралами. Формула Стокса
Нехай
в деякій області, в якій розташовано
поверхню  ,
яка натягнута на контур
,
яка натягнута на контур ,
задано функції
,
задано функції
 ,
,
 ,
які неперервні в цій області разом зі
своїми похідними. Тоді вірна формула
Стокса:
,
які неперервні в цій області разом зі
своїми похідними. Тоді вірна формула
Стокса:

Формула Гріна буде частинним випадком формули Стокса. Якщо поверхневий інтеграл першого типу замінити інтегралом другого типу, то одержимо формулу:


Формулу Стокса зручно записувати за допомогою визначника:
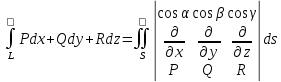
Приклади розв’язання задач:
Приклад
6: Обчислити
інтеграл


Дана
частина поверхні проектується на
площину
 в кільце, розташоване між колами
в кільце, розташоване між колами


 .
Враховуючи,
що
.
Враховуючи,
що

Рис.2.1


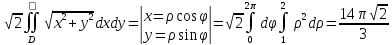
Приклад 7: Обчислити інтеграл

площини
 розташована
в 1 октані та відсічена площиною
розташована
в 1 октані та відсічена площиною
 Із
рівняння поверхні:
Із
рівняння поверхні:
 Проекція площини на
Проекція площини на  –
прямокутник:
–
прямокутник:

 Тоді:
Тоді:
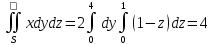
 оскільки
площина паралельна вісі
оскільки
площина паралельна вісі
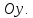
 Із
рівня поверхні:
Із
рівня поверхні:
 Проекція
площини на
Проекція
площини на  –
прямокутник:
–
прямокутник:

 Тоді:
Тоді:
 За
властивістю інтеграла:
За
властивістю інтеграла:


Теорія поля
Якщо
в кожній точці  просторової
області задана скалярна або
векторна
величина, то кажуть, що задано поле цієї
величини, скалярне
просторової
області задана скалярна або
векторна
величина, то кажуть, що задано поле цієї
величини, скалярне  або
векторне
або
векторне  .
.
Основні характеристики полів:
1.
Поверхні (лінії) рівня:

2.
Векторні лінії:
 .
.
3.
Градієнт:
 .
.
4. Потік векторного поля через поверхню:
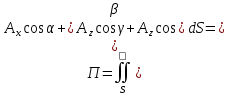

5.
Дивергенція векторного поля: +
+
6. Циркуляція векторного поля вздовж кривої:

7.
Ротор:
 .
Вірна формула Стокса:
.
Вірна формула Стокса:

Основні види полів:
Векторне
поле  називається
потенціальним, якщо існує скалярне
поле
називається
потенціальним, якщо існує скалярне
поле  ,
що
,
що
 Для
того щоб поле було потенціальним ⇔ щоб
Для
того щоб поле було потенціальним ⇔ щоб
 .
.
Векторне
поле  називається
соленоїдальним,
якщо існує векторне поле
називається
соленоїдальним,
якщо існує векторне поле
 ,
що
,
що .
Для того щоб поле було соленоїдальним⇔ щоб
.
Для того щоб поле було соленоїдальним⇔ щоб
 .
.
Довільне векторне поле може бути представлене в вигляді суми потенціального та соленоїдального полів.
Приклади розв’язання задач:
Приклад 8: Знайти дивергенцію векторного поля
 в
точці
в
точці  .
.

Приклад 9: Знайти
потік векторного поля

через
повну поверхню конуса
 двома
способами (безпосередньо і за
формулою
Остроградського).
двома
способами (безпосередньо і за
формулою
Остроградського).
Обчислимо потік безпосередньо. Повна поверхня складається з бічної поверхні
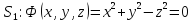 та поверхні основи
та поверхні основи
 .
Тому
.
Тому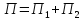 .
.


Із рівняння поверхні маємо:
 ,
,

поверхня
проектується на круг
 Тоді
Тоді


Переходячи до полярних координат, одержимо

Алалогічно,

Тоді одержимо:

Обчислимо потік за формулою Остроградського-Гауса.


Типові завдання
Обчислити криволінійний інтеграл.
Довести, що даний вираз є повним диференціалом функції
 .
.
3.
Знайти
функцію .
.
4. За допомогою формули Гріна обчислити інтеграл.
5.
Обчислити поверхневий інтеграл першого
роду по поверхні  ,
де
,
де  –
частина
площини
–
частина
площини
 ,
яка розташована між координатними
площинами.
,
яка розташована між координатними
площинами.
6. Обчислити поверхневий інтеграл другого роду.
7. Знайти потік векторного поля через зовнішню поверхню піраміди двома способами (безпосередньо і за формулою Остроградського).
8.
Знайти циркуляцію векторного поля
через контур трикутника  ,
утвореного в
результаті
перетину площин, двома способами
(безпосередньо і за формулою
Стокса).
,
утвореного в
результаті
перетину площин, двома способами
(безпосередньо і за формулою
Стокса).
9. З’ясувати, чи є векторне поле соленоїдальним, потенціальним?
