8_12_3276

Математический анализ 11-12 уч. год

Тема 1. Аналитическая геометрия на плоскости

1. Абсцисса точки С, разбивающей отрезок АВ в отношении CBAC , равна

2. Ордината точки С, разбивающей отрезок АВ в отношении CBAC , равна

3. Абсцисса середины отрезка АВ равна

4. В уравнении y kx b значение k – это

координата точки пересечения прямой с осью абсцисс координата точки пересечения прямой с осью ординат

угол, образованный прямой с положительным направлением оси абсцисс тангенс угла, образованного прямой с положительным направлением оси абсцисс

5. В уравнении y kx b значение b – это

координата точки пересечения прямой с осью ОХ угловой коэффициент прямой

координата точки пресечения прямой с осью ОY угол наклона прямой к оси ОХ

6.Прямая Ax C 0 параллельна оси Oy параллельна оси Ох перпендикулярна оси Оy

пересекает ось Оy в одной точке

7.Прямая By C 0

параллельна оси Oy перпендикулярна оси Ох параллельна оси Ох пересекает ось Ох в одной точке

8. Прямая Ax By 0 при B 0

параллельна оси Oy

проходит через начало координат не проходит через начало координат перпендикулярна оси Ох

9. Угол между двумя прямыми определяется формулой tg tg tg

tg k2 k1

1 k1k2

tg k2 k1

1 k1k2

tg k2 k1

1 k1k2

10. Условие параллельности двух прямых имеет вид

1= − 21 121 2= −11= 2

11. Условие перпендикулярности двух прямых имеет вид

1= − 21 12

1 2= − 11= 2

12.Углом между двумя прямыми называется

меньший угол, на который надо повернуть обе прямые до их совпадения с осью ОХ меньший угол, на который надо повернуть одну прямую до ее совпадения с другой прямой

меньший угол, на который надо повернуть обе прямые до их совпадения с осью Оy

разность углов, образованных этими прямыми

13.Уравнение прямой, проходящей через данную точку в данном

направлении, имеет вид y x b

(x2 x1 )(y y1 ) ( y2 y1 )(x x1 ) ax by 1

y – y0= 0(x – x0)

14. В уравнении пучка прямых с центром в точке А угловой коэффициент – фиксированный бесконечный произвольный всегда равен 0

15. Уравнение пучка прямых с центром в точке M 0 x0 ; y0 имеет вид y x b

ax by 1

Ax By C 0 y – y0= (x – x0)

16.Уравнение прямой в отрезках имеет вид

ax by 1 y x b

Ax By C 0 y – y0= 0(x – x0)

17. Общее уравнение прямой имеет вид

Ax By C 0 y x b

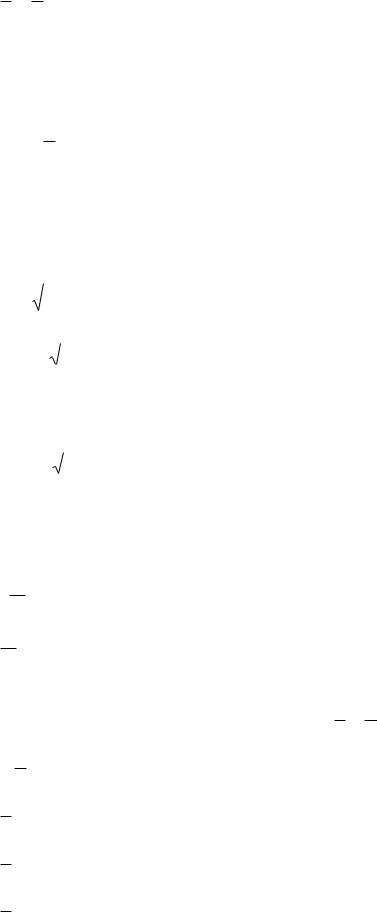
ax by 1

y – y0= 0(x – x0)

18.Уравнение прямой, проходящей через точки A( 2;3) и B(4; 3) , имеет

вид

y 2x 2 y x 5

y x 1 y 2x 1

19.Расстояние от точки до прямой определяется формулой

20. Угловой коэффициент прямой Ax+By+C=O при В 0 равен

A

–A

– BA

A

B

21. Тангенс угла наклона прямой ax by 1 к оси Ох равен

ba

1

a

1

b b

a

22. Уравнение прямой, проходящей через точку A(1;2) параллельно прямой x y 1 0 , имеет вид

y x 5 y x 2 y x 1

28.Уравнение прямой, проходящей через точку B(4;1) и образующей с

положительным направлением оси угол 1350 , имеет вид x y 5 0

x y 3 0 x y 3 0x y 5 0

29.К прямой y 4x 1 перпендикулярна прямая

y 14 x 2

y 14 x 2 y 4x 2

y 4x 3

30. Угол между прямыми 2x 3y 4 0 и 3x 2y 1 0 равен

00

450

900

1350

31.Уравнение прямой, проходящей через точки A(x1 , y1 ) и B(x2 , y2 ) , имеет

вид

32.Расстояние от точки A(2; 1) до прямой 4x 3y 9 0 равно

2,8

4

14

7

33. Из прямых а) x 5y 3 0 ;

б)5x y 4 0; в)5x y 3 0 ;

г) x 5y 3 0 параллельной к прямой y 5x 3 будет

а) в) г) б)

34. Из прямых

а) 2x y 3 0 ;

б) x 2y 3 0 ; в) 2x y 5 0; г) x 2y 3 0

перпендикулярной к прямой y 2x 3 будет

а) б) г) в)

35.Точками пересечения прямой 3x 4y 12 0 с осями координат Ox и Oy являются соответственно точки

A(4;0) и B(0; 3) A(0; 3) и B(4;0) A( 4;3) и B(3; 4) A( 4;0) и B(0;3)

36.Уравнение прямой, проходящей через точки A 2;3 и B 2; 1 , имеет

вид

y2x

y2 x 2

yx 2

37.Уравнение прямой, проходящей через точки A 3; 1 и B 2; 1 , имеет

вид

y3x 2

yx x 1

y1

38. Если x2 x1 , то уравнение прямой, проходящей через точки A x1 ; y1 и B x2 ; y2 , имеет вид

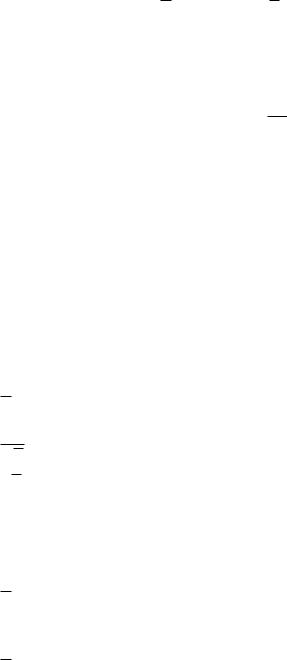
x x1

y x1

y k x x1

y y1

y y1 x x1 x x1

40. Прямые y 34 x 1 и y 34 x 2 параллельны перпендикулярны

образуют угол в 450

образуют угол, равный arctg 247

41.Точка M разбивает отрезок AB , где A 1;2 , B 4;5 , так, что AM 2 MB .

Координаты точки M равны

3;42;32;4

2,5;3,5

42. Расстояние от точки M 3;4 до прямой y 2x 1 равно

1

2

3

1

5 5

43.Угловой коэффициент прямой 2x 3y 6 0 равен

2

3

2

-3

2

3

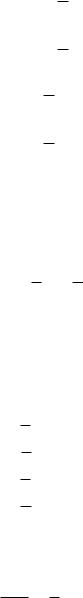
44.Угол наклона прямой 3x 4y 1 0 к положительному направлению

оси Ox равен

arctg 34

arctg 34

arctg 34 arctg 34

45.В треугольнике с вершинами A 3; 2 , B 2;3 , C 4; 1 уравнение

стороны BC имеет вид y 2x 7

y 13 x 73 y x 5

y 4x 3

46. В треугольнике с вершинами A 3; 2 , B 2;3 , C 4; 1 длина медианы AM равна

53

25

35

52

47.Если A 2;3 , B 6; 3 , то точка C , делящая отрезок AB в отношении

CBAC 13 , имеет координаты

48.Уравнение прямой, проходящей через точки A 2;3 и B 2; 1 , имеет

вид

x y 1 0 x y 3 0 x y 1 0 x y 1 0

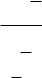
49.В треугольнике с вершинами A 3; 2 , B 2;3 , C 4; 1 уравнение

высоты CD имеет вид x y 3 0

x y 3 0 x y 5 0 x y 5 0

50. В треугольнике с вершинами в точках A 2;3 , B 3; 2 , C 4; 1 длина высоты АD равна

172

5

32

3

18

51.Каноническое уравнение эллипса имеет вид

x 2 2 ( y b)2 R2

(x a)2 y b 0

52.Каноническое уравнение гиперболы имеет вид (2 ответа)

x 2 2 ( y b)2 R2

y a 2 ( y b)2 R2

y b 2 x a 0

53.Каноническое уравнение параболы имеет вид (2 ответа)