Модели временных рядов (Задачи)
На основе помесячных данных за последние 6 лет была построена аддитивная модель временного потребления тепла. Скорректированные значения сезонной компоненты приведены в таблице:
|
Январь |
+ 30 |
Май |
- 20 |
сентябрь |
- 10 |
|
февраль |
+ 25 |
Июнь |
- 34 |
октябрь |
+ 12 |
|
март |
? |
Июль |
- 42 |
ноябрь |
+22 |
|
апрель |
- 2 |
Август |
- 18 |
декабрь |
+28 |
Уравнение тренда выглядит так:
Значение сезонной компоненты за март, а также точечный прогноз потребления тепла на 1 квартал следующего года равны:
+9; 1290,4
—-9; 1290,4
—9; 1226,4
—12; 1226,4
На основе помесячных данных за последние 5 лет была построена аддитивная модель временного потребления тепла. Скорректированные значения сезонной компоненты приведены в таблице:
|
Январь |
+ 17 |
май |
- 20 |
сентябрь |
- 10 |
|
февраль |
+ 15 |
июнь |
- 34 |
октябрь |
? |
|
март |
+ 10 |
июль |
- 42 |
ноябрь |
+22 |
|
апрель |
- 4 |
август |
- 18 |
декабрь |
+27 |
Уравнение тренда выглядит так:
Значение сезонной компоненты за октябрь, а также точечный прогноз потребления тепла на 1 квартал следующего года равны:
+37; 1615,2
—-37; 1615,2
—37; 1845
—4; 1845
На основе помесячных данных за последние 8 лет была построена аддитивная модель временного потребления тепла. Скорректированные значения сезонной компоненты приведены в таблице:
|
Январь |
+ 42 |
Май |
- 10 |
сентябрь |
- 10 |
|
февраль |
+ 21 |
Июнь |
- 50 |
октябрь |
+ 12 |
|
март |
? |
Июль |
- 35 |
ноябрь |
+22 |
|
апрель |
- 1 |
Август |
- 16 |
декабрь |
+28 |
Уравнение тренда выглядит так:
Значение сезонной компоненты за март, а также точечный прогноз потребления тепла на 1 квартал следующего года равны:
+-3; 1611,6
—3; 1617,6
—3; 1526,4
—7; 1226,4
На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:
I квартал – 1,6
II квартал – 0,8
III квартал – 0,7
IV квартал - ?
Уравнение тренда имеет вид:
Значение сезонной компоненты за IV квартал и прогноз на II и III кварталы следующего года равны:
+0,90; 5,28 и 4,55
—1,00; 10,72 и 5,28
—0,90; 4,55 и 5,28
—0,80; 5,28 и 10,72
На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:
I квартал – 1,5
II квартал – ?
III квартал – 0,6
IV квартал – 0,8
Уравнение тренда имеет вид:
Значение сезонной компоненты за II квартал и прогноз на II и III кварталы следующего года равны:
+1,10; 16,06 и 8,82
—1,20; 21,75 и 16,06
—1,10; 8,82 и 16,06
—1,00; 16,06 и 21,75
На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:
I квартал – 1,2
II квартал – 0,8
III квартал – ?
IV квартал – 1,4
Уравнение тренда имеет вид:
Значение сезонной компоненты за III квартал и прогноз на II и III кварталы следующего года равны:
+0,60; 4,32 и 3,12
—0,70; 6,72 и 4,32
—0,60; 3,12 и 4,32
—0,50; 4,32 и 6,72
На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:
I квартал – 1,2
II квартал – 0,9
III квартал – 0,5
IV квартал - ?
Уравнение тренда имеет вид:
Значение сезонной компоненты за IV квартал и прогноз на II и III кварталы следующего года равны:
+1,40; 1,71 и 0,85
—1,60; 7,48 и 4,57
—1,40; 1,36 и 4,57
—1,30; 2,28 и 7,48
На основе поквартальных данных построена мультипликативная модель некоторого временного ряда. Скорректированные значения сезонной компоненты равны:
I квартал – 1,5
II квартал – 0,7
III квартал – ?
IV квартал – 1,2
Уравнение тренда имеет вид:
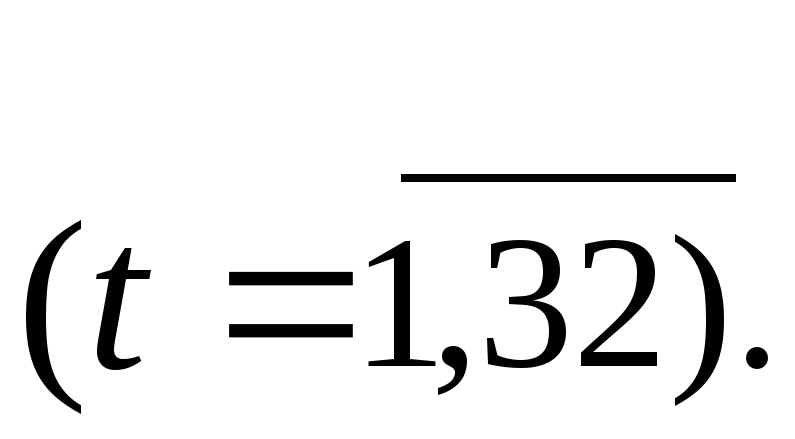
Значение сезонной компоненты за III квартал и прогноз на II и III кварталы следующего года равны:
+0,60; 4,55 и 3,78
—0,70; 6,72 и 4,55
—0,60; 3,78 и 4,55
—0,50; 4,55 и 6,72
На
основе квартальных данных объемов
продаж 1995 – 2000гг. была построена
аддитивная модель временного ряда.
Трендовая компонента имеет вид
Показатели за 2000 г. приведены в таблице:
|
Квартал |
Фактический объем продаж |
Компонента аддитивной модели |
||
|
трендовая |
сезонная |
случайная |
||
|
1 |
270 |
|
|
-9 |
|
2 |
|
|
10 |
+4 |
|
3 |
310 |
|
40 |
|
|
4 |
|
|
S4 |
|
|
ИТОГО: |
2000 |
|
|
|
Отдельные недостающие данные в таблице равны:
+
—
—
—
На
основе квартальных данных объемов
продаж 1995 – 2000гг. была построена
аддитивная модель временного ряда.
Трендовая компонента имеет вид
Показатели за 1999 г. приведены в таблице:
|
Квартал |
Фактический объем продаж |
Компонента аддитивной модели |
||||
|
трендовая |
сезонная |
случайная |
||||
|
1 |
200 |
|
|
-11 |
||
|
2 |
|
|
15 |
+5 |
||
|
3 |
250 |
|
35 |
|
||
|
4 |
|
|
S4 |
|
||
|
Итого |
1000 |
|
|
|
||
Отдельные недостающие данные в таблице равны:
+
—
—
—
На
основе квартальных данных объемов
продаж 1995 – 2000гг. была построена
аддитивная модель временного ряда.
Трендовая компонента имеет вид
Показатели за 1999 г. приведены в таблице:
|
Квартал |
Фактический объем продаж |
Компонента аддитивной модели |
|||
|
трендовая |
сезонная |
случайная |
|||
|
1 |
250 |
|
|
-11 |
|
|
2 |
|
|
15 |
+5 |
|
|
3 |
280 |
|
35 |
|
|
|
4 |
|
|
S4 |
|
|
|
Итого |
1200 |
|
|
|
|
Отдельные недостающие данные в таблице равны:
+
—
—
—
На
основе квартальных данных объемов
продаж 1995 – 2000гг. была построена
аддитивная модель временного ряда.
Трендовая компонента имеет вид
Показатели за 1999 г. приведены в таблице:
|
Квартал |
Фактический объем продаж |
Компонента аддитивной модели |
|||
|
трендовая |
сезонная |
случайная |
|||
|
1 |
280 |
|
|
-11 |
|
|
2 |
|
|
15 |
+5 |
|
|
3 |
320 |
|
30 |
|
|
|
4 |
|
|
S4 |
|
|
|
Итого |
1300 |
|
|
|
|
Отдельные недостающие данные в таблице равны:
+
—
—
—
На
основе квартальных данных объемов
продаж 1996 – 2000гг. была построена
аддитивная модель временного ряда.
Трендовая компонента имеет вид
Показатели за 1999 г. приведены в таблице:
|
Квартал |
Фактический объем продаж |
Компонента аддитивной модели |
||
|
трендовая |
сезонная |
случайная |
||
|
1 |
100 |
|
|
-10 |
|
2 |
|
|
15 |
+3 |
|
3 |
240 |
|
35 |
|
|
4 |
|
|
S4 |
|
|
ИТОГО: |
1050 |
|
|
|
Отдельные недостающие данные в таблице равны:
+
—
—
—
На
основе квартальных данных объемов
продаж 1993 – 2002гг. была построена
аддитивная модель временного ряда.
Трендовая компонента имеет вид
Показатели за 1997 г. приведены в таблице:
|
Квартал |
Фактический объем продаж |
Компонента аддитивной модели |
||
|
трендовая |
сезонная |
случайная |
||
|
1 |
290 |
|
|
-6 |
|
2 |
|
|
9 |
+8 |
|
3 |
270 |
|
14 |
|
|
4 |
|
|
S4 |
|
|
ИТОГО: |
1000 |
|
|
|
Отдельные недостающие данные в таблице равны:
+
—
—
—
Дана таблица:
|
Момент времени |
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
85 |
100 |
120 |
135 |
___ |
где
ожидаемый и действительный объемы
предложения. В соответствии с моделью
адаптивных ожиданий, где
,
значения 
соответственно равны:
+76,75; 87,21; 101,97; 116,83
—78,25; 90,21; 105,25; 120,14
—76,75; 87,21; 105,25;120,14
—78,25; 90,21; 106,60; 122,22
Дана таблица:
|
Момент времени |
|
|
|
|
|
|
|
130 |
|
|
|
|
|
|
145 |
165 |
190 |
210 |
___ |
где
ожидаемый и действительный объемы
предложения. В соответствии с моделью
адаптивных ожиданий, где
,
значения 
соответственно равны:
+138,25; 152,96; 173,33; 193,50
—136,75; 149,46; 169,63; 189,83
—138,25; 152,96; 169,63; 189,83
—136,75; 149,46; 167,70; 186,74
Дана таблица:
|
Момент времени |
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
95 |
120 |
150 |
165 |
___ |
где
ожидаемый и действительный объемы
предложения. В соответствии с моделью
адаптивных ожиданий, где
,
значения
соответственно равны:
+79,25; 101,66; 128,25; 148,46
—78,25; 90,21; 135,46; 120,14
—79,25; 101,66; 135,46;120,14
—78,25; 90,21; 106,74; 122,22
Дана таблица:
|
Момент времени |
|
|
|
|
|
|
|
135 |
|
|
|
|
|
|
140 |
165 |
190 |
210 |
___ |
где
ожидаемый и действительный объемы
предложения. В соответствии с моделью
адаптивных ожиданий, где
,
значения
соответственно равны:
+138,25; 155,64; 177,97; 198,79
—136,75; 149,46; 169,63; 189,83
—138,25; 155,64; 169,63; 189,83
—136,75; 149,46; 167,70; 186,74
Дана таблица:
|
Момент времени |
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
135 |
145 |
155 |
175 |
___ |
где
ожидаемый и действительный объемы
предложения. В соответствии с моделью
адаптивных ожиданий, где
,
значения
соответственно равны:
+126,00; 133,60; 142,16; 155,30
—125,00; 131,50; 141,50; 152,74
—126,00; 133,60; 141,50; 152,74
—125,00; 131,50; 136,16; 149,70
На основе помесячных данных за последние 4 года была построена аддитивная модель временного потребления тепла. Скорректированные значения сезонной компоненты приведены в таблице:
|
Январь |
+ 30 |
май |
- 20 |
сентябрь |
- 10 |
|
февраль |
+ 25 |
июнь |
- 34 |
октябрь |
? |
|
март |
+ 15 |
июль |
- 42 |
ноябрь |
+22 |
|
апрель |
- 2 |
август |
- 18 |
декабрь |
+27 |
Уравнение тренда выглядит так:
Значение сезонной компоненты за октябрь, а также точечный прогноз потребления тепла на 1 квартал следующего года равны:
+7; 1315
—-7; 1315
—7; 1245
—10; 1245
На основе квартальных данных с 2000 г. по 2004 г. получено уравнение y = - 0,67 + 0,0098 x t1 – 5,62 x t2 + 0,044 x t3
ESS =110,3, RSS = 21,4 (ESS – объясненная сумма квадратов, RSS – остаточная сумма квадратов)
В уравнение были добавлены три фиктивные переменные, соответствующие трем первым кварталам года, величина ESS увеличилась до 120,2. Проверьте гипотезу о сезонности (α =0,05):
+гипотезу об отсутствии сезонности отвергаем, т.к. F=3,73 (>Fкр)
—гипотезу об отсутствии сезонности отвергаем, т.к. F=4,2 (>Fкр)
—гипотезу о наличии сезонности отвергаем, т.к. F=3,73 (<Fкр)
—гипотезу о наличии сезонности отвергаем, т.к. F=4,2 (<Fкр)
На основе квартальных данных с 1991 г. по 2004 г. получено уравнение y = - 0,55 + 0,088 x t1 – 4,77 x t2 + 5,4 x t3
ESS =90,4, RSS = 21,4 (ESS – объясненная сумма квадратов, RSS – остаточная сумма квадратов)
В уравнение были добавлены три фиктивные переменные, соответствующие трем первым кварталам года, величина ESS увеличилась до 92. Проверьте гипотезу о сезонности (α =0,05):
+гипотезу об отсутствии сезонности отвергаем, т.к. F=4,31 (>Fкр)
—гипотезу об отсутствии сезонности отвергаем, т.к. F=3,2 (>Fкр)
—гипотезу о наличии сезонности отвергаем, т.к. F=1,31 (<Fкр)
—гипотезу о наличии сезонности отвергаем, т.к. F=2,2 (<Fкр)
На основе квартальных данных с 2001 г. по 2003 г. получено уравнение y = - 0,55 + 1,8 x t1 – 2,7 x t2 + 3,4 x t3
ESS =115,3, RSS = 10,2 (ESS – объясненная сумма квадратов, RSS – остаточная сумма квадратов)
В уравнение были добавлены две фиктивные переменные, соответствующие двум первым кварталам года, величина ESS увеличилась до 120. Проверьте гипотезу о сезонности (α =0,05):
—гипотезу об отсутствии сезонности отвергаем, т.к. F=8,7 (>Fкр)
—гипотезу об отсутствии сезонности отвергаем, т.к. F=2,6 (>Fкр)
—гипотезу о наличии сезонности отвергаем, т.к. F=8,7 (<Fкр)
+гипотезу о наличии сезонности отвергаем, т.к. F=2,6 (<Fкр)
На основе квартальных данных с 2000 г. по 2002 г. получено уравнение y = 1,55 + 1,4 x t1 – 0,77 x t2 + 2,4 x t3
ESS = 82, RSS = 12 (ESS – объясненная сумма квадратов, RSS – остаточная сумма квадратов)
В уравнение были добавлены три фиктивные переменные, соответствующие трем первым кварталам года, величина ESS увеличилась до 90. Проверьте гипотезу о сезонности (α =0,05):
—гипотезу об отсутствии сезонности отвергаем, т.к. F=4,3 (>Fкр)
—гипотезу об отсутствии сезонности отвергаем, т.к. F=3,3 (>Fкр)
—гипотезу о наличии сезонности отвергаем, т.к. F=4,3 (<Fкр)
+гипотезу о наличии сезонности отвергаем, т.к. F=3,3 (<Fкр)
Модель зависимости объемов продаж компании от расходов на рекламу имеет вид y = - 0,67 + 4,5 x t + 3 x t-1 + 1,5 x t-2 + 0,5 x t-3
Краткосрочный, долгосрочный мультипликатор и средний лаг равны:
—краткосрочный 0,5 , долгосрочный 9,5, средний лаг 2,3
+краткосрочный 4,5 , долгосрочный 9,5, средний лаг 0,79
—краткосрочный -0,67 , долгосрочный 9,5, средний лаг 0,79
Модель зависимости объемов продаж компании от расходов на рекламу имеет вид y = -0,31 + 1,5 x t + 3 x t-1 + 4,5 x t-2 + 0,5 x t-3
Краткосрочный, долгосрочный мультипликатор и средний лаг равны:
—краткосрочный 0,5 , долгосрочный 9,2, средний лаг 2,3
+краткосрочный 1,5 , долгосрочный 9,5, средний лаг 0,791
—краткосрочный -0,67 , долгосрочный 9,2, средний лаг 0,7
Модель зависимости объемов продаж компании от расходов на рекламу имеет вид y = 0,27 +1,23 x t + 0,963 x t-1 +0,77 x t-2 + 1,04 x t-3
Краткосрочный, долгосрочный мультипликатор и средний лаг равны:
—краткосрочный 0,27 , долгосрочный 2,2, средний лаг 2,3
+краткосрочный 1,23 , долгосрочный 4, средний лаг 1,41
—краткосрочный 1,04, долгосрочный 2, средний лаг 0,7
Модель зависимости объемов продаж компании от расходов на рекламу имеет вид y = -1,6 + 0,5 x t + 3,3 x t-1 + 5,5 x t-2 + 1,5 x t-3
Краткосрочный, долгосрочный мультипликатор и средний лаг равны:
—краткосрочный 0,5 , долгосрочный 9,2, средний лаг 2,3
+краткосрочный 0,5 , долгосрочный 10,8, средний лаг 1,74
—краткосрочный -0,67 , долгосрочный 9,2, средний лаг 0,7
На основе квартальных данных получено уравнение множественной регрессии
y = - 0,67 + 0,0098 x t1 – 5,62 x t2 + 0,044 x t3
и ESS = 120,32, RSS = 41,4. (ESS – объясненная сумма квадратов, RSS – остаточная сумма квадратов). Для этой же модели были раздельно проведены регрессии на основе данных:
1-й квартал 1991 г. - 1-й квартал 1995 г. и
2-й квартал 1995 г. – 4 квартал 1996 г., соответственно получены следующие значения сумм квадратов остатков RSS1 = 22,25, RSS2=12,32. Гипотеза о том, что произошли структурные изменения на уровне α =0,05:
—подтвердилась, т.к. F = 1,8 , что больше F кр
+не подтвердилась, т.к. F = 0,8 , что меньше F кр
—подтвердилась, т.к F = 3,54, что больше F кр
На основе квартальных данных получено уравнение множественной регрессии
y = - 0,55 + 0,088 x t1 – 4,77 x t2 + 5,4 x t3
и ESS = 110,32, RSS = 21,43. (ESS – объясненная сумма квадратов, RSS – остаточная сумма квадратов). Для этой же модели были раздельно проведены регрессии на основе данных:
1-й квартал 1991 г. - 1-й квартал 1995 г. и
2-й квартал 1995 г. – 4 квартал 1996 г., соответственно получены следующие значения сумм квадратов остатков RSS1 = 12,25, RSS2=2,32. Гипотеза о том, что произошли структурные изменения на уровне α =0,05:
—подтвердилась, т.к. F = 1,883 , что больше F кр
+не подтвердилась, т.к. F = 1,883 , что меньше F кр
—подтвердилась, F = 3,54, что больше F кр
На основе квартальных данных получено уравнение множественной регрессии
y = 1,55 + 1,4 x t1 – 0,77 x t2 + 2,4 x t3
и ESS = 92,32, RSS = 22,3. (ESS – объясненная сумма квадратов, RSS – остаточная сумма квадратов). Для этой же модели были раздельно проведены регрессии на основе данных:
1-й квартал 1991 г. - 1-й квартал 1995 г. и
2-й квартал 1995 г. – 4 квартал 1996 г., соответственно получены следующие значения сумм квадратов остатков RSS1 = 6,78, RSS2=2,2. Гипотеза о том, что произошли структурные изменения на уровне α =0,05:
+подтвердилась, т.к. F = 5,93 , что больше F кр
—не подтвердилась, т.к. F = 1,883 , что меньше F кр
—подтвердилась, т.к F = 3,54, что больше F кр
На основе квартальных данных с 1991 года по 1996 год с помощью МНК получено следующее уравнение:
Y t = 1,12 – 0, 0098 x t1 – 5, 62 x t2 + 0, 044 x t3
(2,14) (0,0034) (3,42) (0,009)
В скобках указаны стандартные ошибки, ESS (объясненная сумма квадратов) = 115, 32; RSS (остаточная сумма квадратов) = 25, 43
Когда в уравнение были добавлены три фиктивные переменные, соответствующие первым трем кварталам года, величина ESS выросла до 128, 20. Проверьте гипотезу о наличии сезонности при уровне значимости α = 0,05:
—гипотеза о наличии сезонности отвергается
+гипотеза о наличии сезонности принимается
—на основе имеющихся данных такую гипотезу проверить невозможно
На основе квартальных данных с 1991 года по 1996 год с помощью МНК получено следующее уравнение:
Y t = 1,12 – 0, 0098 x t1 – 5, 62 x t2 + 0, 044 x t3
(2,14) (0,0034) (3,42) (0,009)
В скобках указаны стандартные ошибки, ESS (объясненная сумма квадратов) = 116, 32; RSS (остаточная сумма квадратов) = 31, 43
Проверьте значимости коэффициентов и модели в целом при уровне значимости α = 0,05:
—все коэффициенты модели значимы и модель в целом также значима
+модель в целом значима, но часть коэффициентов незначима
—все коэффициенты незначимы и модель также статистически незначима
—на основе имеющихся данных проверить такие гипотезы невозможно