7. Геометрические и кинематические параметры зубчатых передач

1. Цилиндрические зубчатые колеса. Рассмотрим вначале наиболее простую цилиндрическую зубчатую передачу — прямозубую (рис. 5). Часть зубчатого колеса, на которой расположены зубья, называется венцом; часть, насаживаемая на вал, называется ступицей. Делительная окружность, име­ющая диаметр d, делит зуб по высоте на две части — головку высотой ha и ножку высотой hfi при этом высота зуба h = ha + hf. Расстояние Р между одноименными профилями соседних зубьев, измеренное по дуге делительной окружности, называется окруж­ным делительным шагом зубьев; он складывается из окружной толщины зуба S и ширины впадины е. Величина т, имеющая размер­ность длины и равная т = Р/п, (Рис.5) называется окружным делительным модулем, или просто модулем. Модуль — один из основных параметров зубчатого колеса; ко­леса, находящиеся в зацеплении друг с другом, должны иметь одинаковый модуль. Модули стандартизованы, и их значения можно узнать из части 5 учебника. В машиностроении чаще всего используются значения модулей от 1 до 14 мм. Все основные параметры зубчатых колес выражают через модуль. Шаг зубьев Р = пт; диаметр делительной окружности d = mz,

(Рис.5) Рис. 5. Цилиндрическое зубчатое колесо с прямыми зубьями:

1 — окружность вершин зубьев; 2 — делительная окружность; 3 — окружность впадин

где z — число зубьев того колеса, делительную окружность которого определяют.

При изготовлении зубчатых колес в качестве исходного рассматривается зацепление коле-

са с зубчатой рейкой. При этом рейка называется номинальной исходной зубчатой рейкой, и контур ее зубьев называют исходным контуром. В соответствии со стандартным исходным контуром для цилиндрических зубчатых колес (рис. 6) высота головки зуба ha = = т, высота ножки зуба h/ = m + c = 1,25m, где с — радиальный зазор; профиль исходного контура в пределах глубины захода hd ~ = 2т прямолинейный; у основания зуба имеется радиус закругления г, = 0,25т. Исходя из сказанного: высота зубьев цилиндрических колесРис. 6. Стандартный исходный контур для цилиндрических зубчатых колесd =2,25m; (Рис.6) диаметр вершин зубьев da = d + 2ha = mz-i = m(z (Рис.7)nдиаметр впадин df=d-2hf =mz-2- (Рис.8) Межосевое делительное расстояние зубчатой передачи(Рис.9)

Знак «-» соответствует внутреннему зацеплению. Если межосевое расстояние отличается от делительного, что также встречается, то обозначается aw.

Расстояние между торцами зубьев Ъ (длина зуба) называется шириной венца (рис. 8.5). В процессе работы прямозубой передачи пара зубьев входит в зацепление сразу по всей длине контакта (теоретически контакт зубьев происходит по линии), что сопро­вождается ударом зубьев друг по другу. Но так как другая пара зубьев, которая уже находилась в зацеплении, еще не вышла из него, в зацеплении находятся две пары зубьев. Затем также одномоментно эта другая пара выходит из зацепления, и в контакте остается только одна пара зубьев. Все это сопровождается изменениями в деформациях зубьев, которые при однопарном зацеплении сильнее, чем при двупарном, вибрациями и другими динамическими нагрузками. Как было уже сказано, продолжительность нахождения передачи в одно- и двупарном зацеплениях зависит оТ коэффициента перекрытия е.

Прямозубая передача имеет только торцовое перекрытие. Коэффициент торцового перекрытия еа (отличается от коэффициента перекрытия еу индексом) равен отношению угла торцового перекрытия фа к угловому шагу т:

£«=Фа/т. (Рис.10)

Для прямозубых передач сра соответствует (pY на рис. 8.3, а коэффициент торцового перекрытия для этих передач рекомендуется принимать еи > 1,2.

Стандартом предусмотрено 12 степеней точности для цилиндрических зубчатых колес, причем первая — наивысшая. Для каждой степени точности установлены нормы кинематической точности, плавности работы и контакта зубьев и передач. В машиностроении передачи общего назначения изготовляют по 6—9-й степеням точности, которые применяют для прямозубых колес при окружных скоростях до 15...2 м/с соответственно.

Наиболее распространены в машиностроении косозубые зубчатые колеса (рис.7). Косозубые передачи с параллельными осями имеют противоположное направление зубьев ведущего и ведомого колес (рис. 7, а) и так же, как и прямозубые, относятся к цилиндри­ческим зубчатым передачам. Отметим для сравнения, что винто-колесные передачи (см. рис. 2.12), оси которых скрещиваются и колеса которых похожи на косозубые, имеют одинаковые направ-

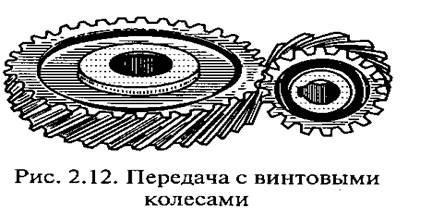
Рис.7. Параметры цилиндрических косозубых зубчатых колес и передач: а — направление зубьев; б — сечение зубьев нормалью

ления зубьев обоих колес; исходный контакт рабочих поверхностей зубьев у них происходит не по линии, а в точке. Если представить себе линию пересечения боковой поверхности зуба косозубого колеса с делительной цилиндрической повер­хностью, то получится винтовая линия постоянного шага. В косозубых колесах эта линия (линия зуба) может иметь правое и левое направление, как винтовая линия резьбы. Угол наклона линии зуба обозначается буквой р. Как видно из рис. 7, а, у косозубых передач контактные линии расположены наклонно по отношению к линии зуба, поэтому в отличие от прямых зубьев косые входят в зацепление не сразу по всей длине, а постепенно. Угол перекрытия косозубого колеса состоит из торцового и осевого углов перекрытия, и коэффициент перекрытия ет косозубой передачи складывается из ко­эффициентов торцового еа и осевого ер перекрытий:

ег =£« +ер > 2. (8.Ц) В отличие от прямозубой передачи у косозубой нет периода од-попарного зацепления. Поэтому эти передачи отличаются существен­но большей прочностью и плавностью работы. Например, для косозубых колес 6—9-й степеней точности допустимы окружные скорости 30...4 м/с соответственно. Так как косозубые колеса обрабатываются теми же зуборезными инструментами, что и прямозубые, стандартные параметры колес задаются в нормальном сечении NN к зубу (рис. 8.7, б). Для косозубых колес используются три модуля: нормальный — т„ = Р„/п, окружной — т, = Р,/п и осевой — тх = Рх/п, где Р„, Р, и Рх — соответственно нормальный шаг, измеренный по делительной ок­ружности; окружной шаг, измеренный по дуге делительной окружности в торцовом сечении; осевой шаг, измеренный по образующей делительного цилиндра.

Как следует из рис. 7, б:

Р, =Р„/соБр; т, =mfl/cosp.

Все размеры зубьев косозубого колеса определяют по нормальному модулю тп:

h = ha + hf = тп + 1,25т„ = 2,25т„, а диаметр делительной окружности — по окружному модулю:

d = m,z- mnz/cosp. (8. И) Другие размеры косозубых колес определяют по формулам: диаметр вершин зубьев da =d + 2ha =d + 2mn; диаметр впадин df =d-2hf =d-2,5mn; межосевое расстояние

a = m,{z + Z2)/2 = mri(zl + ^2)/(2cosp). Коэффициент осевого перекрытия косозубой передачи

где Ь — ширина венца; Рх — осевой шаг.Если ер — целое число, то суммарная длина контактных линий будет все время оставаться постоянной, что положительно отра­жается на работе передачи, так как нагрузка на зубья в процессе зацепления остается постоянной (для сравнения см. сказанное выше о нагрузках на зубья прямозубых колес). Суммарная длина контактных линий косозубой передачи

1г = £ea/cosp. Недостатком косозубых передач можно считать возникающую при работе передачи осевую силу Fa, вызванную углом р и равную

Fa = Ft*b где F; = 2Tjd, здесь Т — передаваемый вращающий момент, d — диаметр делительной окружности. Этот недостаток устраняется в шевронных зубчатых колесах, венец которых по ширине состоит из участков с зубьями с проти­воположными углами наклона (рис.8).

В шевронных колесах осевые силы Fa взаимно уравновешиваются и на опоры валов не передаются. На рис. .8, а показано шевронное зубчатое колесо с дорожкой шириной а посреди венца; так технологичнее нарезать зубья фрезой, но колесо получается

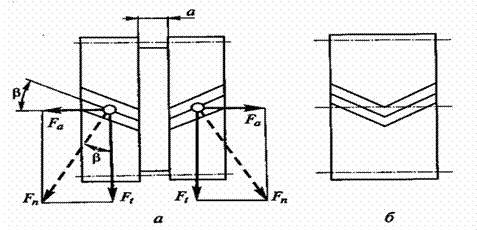Рис.8. Цилиндрическое шевронное зубчатое колесо: а — с дорожкой посередине колеса; б — без дорожки

большой толщины. На рис. 8, £ представлено шевронное колесо без дорожки, изготовление которого затруднительно.

Так как осевые усилия в шевронных колесах уравновешены углы наклона зубьев р могут быть увеличены от 20°, наибольшей их величины для косозубых колес в общем машиностроении, до 40... 45°. При этом плавность работы и ее нагрузочная способность существенно возрастают. Однако шевронные колеса трудоемки в изготовлении и дороги, требуют специфической фиксации в опо­рах. В осевом направлении закрепляется только одно колесо, а сопрягаемое с ним второе колесо должно свободно передвигаться в этом направлении, так как осевая фиксация здесь происходит по зубьям шевронного колеса.