lektsii_1 / модуль4 / несобств интегр

Лекция 4.5. Несобственные интегралы.

1. Интегралы с бесконечными пределами.

Пусть функция f(x) определена и непрерывна на интервале [a, ). Тогда она непрерывна на любом отрезке [a, b].

Определение: Если существует конечный предел , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ).

Обозначение:

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

Аналогичные рассуждения можно привести для несобственных интегралов вида:

.

Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.

Пример 1.

- не существует.

Несобственный интеграл расходится.

Пример 2.

- интеграл сходится

Признаки сходимости и расходимости:

1) Если для всех х (x  a) выполняется условие и интеграл сходится, то тоже сходится и  .

2) Если для всех х (x  a) выполняется условие и интеграл расходится, то тоже расходится.

3) Если сходится, то сходится и интеграл . В этом случае интеграл называется абсолютно сходящимся.

Пр.3. Исследовать на сходимость: .

Так как , то . - полученный интеграл является сходящимся. Согласно признаку (1) интеграл так же является сходящимся.

2. Интегралы от неограниченных функций.

Несобственные интегралы от функций с бесконечными разрывами также определяются посредством предельного перехода.

Пусть функция непрерывна при и , то 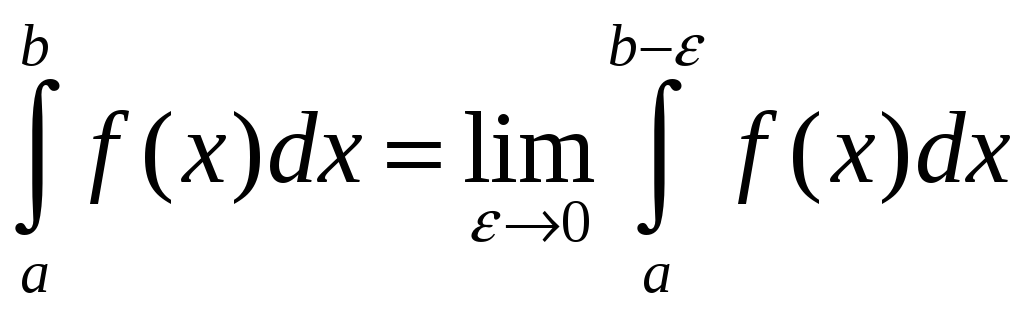. Если существует конечный предел в правой части формулы, то несобственный интеграл называется сходящимся.

Аналогичным образом определяется интеграл от функции , если :

.

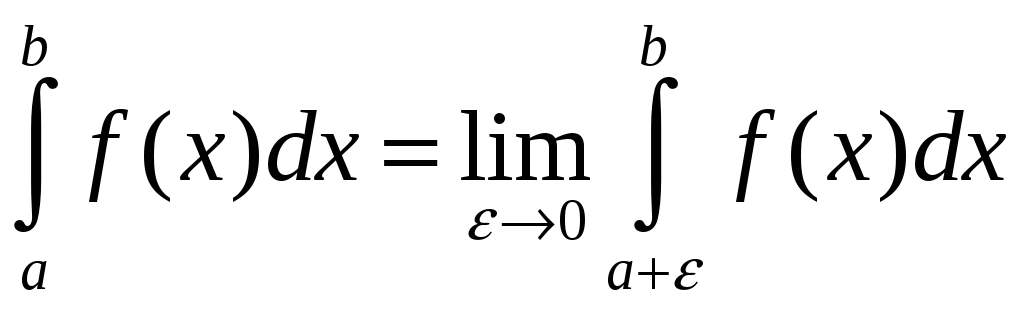Если функция f(x) имеет разрыв в точке c на промежутке [a, b], то

Таких точек внутри отрезка может быть несколько. Если сходятся все интегралы, входящие в сумму, то сходится и суммарный интеграл.

Пр.1. .

Пр.2

Интегралы I₁ и I₂ сходящиеся, следовательно и так же сходящийся.

Пр.3

.

! В результате замены переменной данный несобственный интеграл от функции, имеющий бесконечный разрыв в точке x = 2, преобразовался в собственный интеграл от непрерывной фнкции с конечным интервалом интегрирования.

Признаки сходимости и расходимости:

1. Признак сравнения.

Если на интервале [a, b) функции и непрерывны, в точке x = b имеют разрыв второго рода и удовлетворяют условию , то

а) из сходимости следует сходимость ;

в) из расходимости следует расходимость .

2. Предельный признак сравнения.

Пусть функции и непрерывны на интервале [a, b) и в точке x = b имеют разрыв второго рода. Если существует предел , то и сходятся или расходятся одновременно.