Часть 2 основы электромеханики

ОГЛАВЛЕНИЕ ВТОРОЙ ЧАСТИ

Глава 6 элетромагнитые и электромашинные устройства 198

6.1. Цепи с взаимной индуктивностью 198

6.1.1. Понятие о взаимной индуктивности 198

6.1.2. Эквивалентные преобразования участков цепей со связанными индуктивностями 204

6.2. Трансформаторы 210

6.2.1. Назначение и устройство трансформатора 210

6.2.2. Принцип действия трансформатора 211

6.2.3. Уравнения и схемы замещения трансформатора 215

6.2.4. Экспериментальное определение параметров схемы замещения трансформатора 218

6.2.5. Нагрузочный режим, КПД трансформатора 220

6.2.6. Частотные и временные характеристики импульсного трансформатора 222

6.3. Назначение и классификация электромашинных устройств. Машины постоянного тока. Асинхронные машины. Синхронные машины 227

6.3.1. Назначение и классификация электрических машин 227

6.3.2. Преобразование энергии в электрических машинах 228

6.3.3. Принцип действия и устройство коллекторных машин постоянного тока 233

6.3.4. Принцип действия и устройство электрических машин переменного тока 235

6.3.5 Генераторы постоянного тока 245

6.3.6. Синхронные генераторы 249

6.3.7. Общая характеристика электрических двигателей 256

6.3.8. Двигатели постоянного тока 258

6.3.9. Асинхронные двигатели 268

6.3.10. Синхронные двигатели 275

Глава 6 элетромагнитые и электромашинные устройства

6.1. Цепи с взаимной индуктивностью

6.1.1. Понятие о взаимной индуктивности

Две или более индуктивных катушек называются связанными, если изменение тока в одной из катушек вызывает появление ЭДС в остальных катушках. Напомним, что явление наведения ЭДС в какой-либо индуктивной катушке при изменении тока другой катушки называется взаимоиндукцией, а наведенная ЭДС – ЭДС взаимоиндукции.

Рассмотрим две индуктивные катушки, расположенные таким образом, что магнитный поток, вызванный током в одной из катушек, пронизывает витки другой катушки (рис. 6.1).
	Рис. 6.1

Пусть i₁ и i₂ - токи первой и второй катушек; Ф₁₁ и Ф₂₂ – магнитные потоки самоиндукции этих катушек, т.е. магнитные потоки, пронизывающие каждую из катушек и вызванные протекающим по ней током. Часть магнитного потока самоиндукции первой катушки Ф₂₁, которая пронизывает витки второй катушки, называется потоком взаимоиндукции второй катушки. Часть магнитного потока самоиндукции первой катушки Ф_S1, которая не пронизывает витки второй катушки, называется потоком рассеяния первой катушки. Часть магнитного потока самоиндукции второй катушки Ф₁₂, которая пронизывает витки первой катушки, называется потоком взаимоиндукции первой катушки. Часть магнитного потока самоиндукции второй катушки Ф_S2, которая пронизывает витки только второй катушки, называется потоком рассеяния второй катушки. Таким образом, магнитный поток самоиндукции каждой катушки содержит по две составляющие: Ф₁₁=Ф₂₁+Ф_S1; Ф₂₂=Ф₁₂+Ф_S2.

Полный магнитный поток, пронизывающий каждую из катушек, складывается из магнитных потоков самоиндукции и взаимоиндукции:

Ф₁=Ф₁₁Ф₁₂; Ф₂=Ф₂₂Ф₂₁.

Потокосцепление каждой из катушек так же имеет две составляющие: ₁=₁₁₁₂; ₂=₂₂₂₁.

Когда все витки каждой катушки пронизываются одинаковыми магнитными потоками, можно написать: ₁=N₁(Ф₁₁Ф₁₂); ₂=N₂(Ф₂₂Ф₂₁), где N₁, N₂ – число витков первой и второй катушек.

Знак плюс в приведенных выше выражениях берется в том случае, когда магнитные потоки самоиндукции и взаимоиндукции каждой катушки совпадают по направлению. Такое включение катушек индуктивности называется согласным.

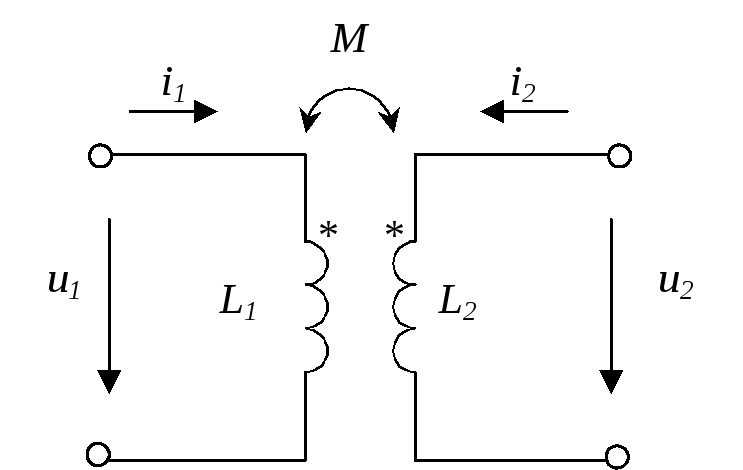
Знак минус ставится в том случае, когда магнитные потоки самоиндукции и взаимоиндукции имеют противоположные направления. Такое включение катушек называется встречным (рис. 6.2)

В соответствии с законом электромагнитной индукции ЭДС, наводимые в каждой из связанных катушек индуктивности,

.

	Первое слагаемое в этих выражениях представляет собой ЭДС самоиндукции, второе – ЭДС взаимоиндукции. Преобразуем последнее выражение:
Рис. 6.2

.

В индуктивных катушках без ферромагнитных сердечников магнитные потоки самоиндукции и взаимоиндукции пропорциональны вызывающим их токам, поэтому производные потокосцеплений по токам могут быть заменены отношением соответствующих величин.

Индуктивность каждой катушки L₁ и L₂ есть отношение потокосцепления самоиндукции к вызвавшему его току:

.

Взаимные индуктивности между катушками М₁₂ и М₂₁ есть отношение потокосцепления взаимоиндукции к вызвавшему его току:

.

Связанные индуктивные катушки, у которых потоки самоиндукции и взаимоиндукции пропорциональны вызвавшим их токам, называются катушками с линейной индуктивностью. Для них всегда выполняется условие М₁₂ = М₂₁=М. Взаимная индуктивность измеряется в генри (Гн).

С учетом введенных обозначений ЭДС, наводимые в каждой катушке: .

Переходя от ЭДС к напряжениям на зажимах связанных индуктивных катушек, окончательно получаем

.

При анализе цепей с взаимной индуктивностью возникает вопрос, каким образом (согласно или встречно) по отношению к выбранным условным положительным направлениям токов включены рассматриваемые индуктивные катушки и в соответствии с этим какой знак (плюс или минус) необходимо использовать в выражениях. Если конструкции индуктивных катушек, в частности направления их намотки, известны, а направления токов заданы, то для выбора знака в приведенных выражениях достаточно, воспользовавшись правилом буравчика, определить направления магнитных потоков самоиндукции каждой из катушек. Например, применяя правило буравчика, устанавливаем, что у катушек (рис.6.1) направления магнитных потоков самоиндукции и взаимоиндукции у каждой катушки одинаковы, а у катушек (рис. 6.2) – противоположны.

При изображении принципиальных схем цепей с взаимной индуктивностью условные графические обозначения индуктивных катушек не отражают особенностей их конструкции. Для выяснения, является ли данное включение катушек согласным или встречным, вводится понятие одноименных зажимов связанных индуктивных катушек.

Одноименными зажимами двух связанных индуктивных катушек называется пара зажимов, выбранных таким образом, что при одинаковых относительно этих зажимов направлениях токов катушек магнитные потоки самоиндукции и взаимоиндукции в каждой из них суммируются. Одноименные зажимы индуктивных катушек помечаются одинаковыми значками (буквами н, к; точками, звездочками, треугольниками и т.п.), проставляемыми в непосредственной близости к соответствующим зажимам. Так, например, на рис. 6.1 одноименные зажимы помечены звездочками, а на рис. 6.2 – точками.

Аналогично поступают и при построении схем замещения электрических цепей с взаимными индуктивностями. Условное графическое изображение связанных индуктивностей, используемое при построении таких схем, приведено на рис.6.3.
	Рис. 6.3

Таким образом, если токи связанных индуктивностей одинаково ориентированы относительно одноименных зажимов, то такое включение является согласным и в приведенных ранее выражениях следует взять знак плюс; в противном случае включение является встречным и необходимо использовать знак минус. На рис. 6.3. индуктивности включены согласно.

Из качественного рассмотрения процессов в связанных индуктивных катушках следует, что чем сильнее связаны катушки, т.е. чем большая часть магнитного потока, создаваемого током каждой из них, пронизывает другую катушку, тем выше взаимная индуктивность. Однако при этом неясно, как связана взаимная индуктивность с индуктивностями катушек и чем определяется максимальное значение М. Введем новую величину, количественно характеризующую степень связи между катушками, - коэффициент связи.

Коэффициент связи представляет собой среднее геометрическое отношений потока взаимоиндукции к потоку самоиндукции каждой из катушек .

Представляя поток самоиндукции каждой катушки в виде суммы потока рассеяния этой катушки и потока взаимоиндукции другой катушки, получаем .

Из этого выражения следует, что значения коэффициента связи лежат в пределах , причем максимальное значениебудет иметь место только в том случае, когда потоки рассеяния обеих катушек равны нулю, или, другими словами, когда магнитный поток, создаваемый током одной катушки, полностью пронизывает другую катушку. Коэффициент связи зависит от конструкции катушек и на практике всегда.

Коэффициент связи можно выразить через индуктивности связанных катушек и их взаимную индуктивность: , откуда следует, что. Таким образом, максимальное значение взаимной индуктивности катушек не может превышать среднего геометрического их индуктивностей.

Для анализа цепей с взаимной индуктивностью при гармоническом воздействии можно воспользоваться методом комплексных амплитуд. Переходя от мгновенных токов и напряжений к их комплексным изображениям и принимая во внимание, что дифференцированию гармонических функций времени соответствует умножение их изображений на , можно получить уравнения связанных индуктивностей в комплексной форме:

.

Комплексное действующее значение напряжения на каждой из связанных индуктивностей помимо напряжения на комплексном сопротивлении индуктивности , вызванного ее током, содержит также дополнительный член, который можно рассматривать как напряжение на некотором комплексном сопротивлении, называемом сопротивлением связи, вызванное током другой индуктивности:

.

Комплексная схема замещения пары связанных индуктивностей приведена на рис. 6.4. Система уравнений электрического равновесия цепи с взаимными индуктивностями, так же, как и системы уравнений ранее рассмотренных цепей, не содержащих
	Рис. 6.4

взаимных индуктивностей, формируется из уравнений баланса токов и напряжений, составленных на основании законов Кирхгофа. При произвольном внешнем воздействии соответствующие уравнения составляются для мгновенных значений токов и напряжений, при гармоническом воздействии – для их комплексных изображений. Напомним, что вид и число уравнений, составляемых на основании законов Кирхгофа, определяется только топологией цепи и не зависит от входящих в нее элементов. В связи с этим уравнения баланса токов и напряжений цепи, содержащей связанные индуктивности, имеют такой же вид, как и уравнения соответствующей цепи в отсутствии связи между индуктивностями, а в число уравнений наряду с уравнениями других элементов входят уравнения связанных индуктивностей.