
- •ВВЕДЕНИЕ
- •ТЕМАТИЧЕСКИЙ ПЛАН КУРСА
- •СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ
- •УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ
- •Лист 1
- •Лист 2
- •Лист 3
- •Таблица 4
- •Описание предмета к листу 3
- •Таблица 5
- •Лист 4
- •Лист 5
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •Приложение А
- •Приложение Б
- •Приложение В
- •Приложение Г
- •Изображения на чертеже – виды, разрезы, сечения
- •(ГОСТ 2.305–2008)
- •Приложение Д
- •Приложение Е
- •Приложение Ж
- •Редактор Е.Г. Козвонина
- •Текст напечатан с оригинала-макета, представленного авторами.
15
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ
Лист 1
Построить три проекции пирамиды и линии сечения пирамиды про-
ецирующей плоскостью α. Построить развертку боковой поверхности усе-
ченной пирамиды.
Варианты задания приведены в табл. 3.
Примеры выполнения листа1 представлены в приложении Ж
(рис. Ж2 и Ж3).
Построение трех проекций пирамиды
илинии сечения ее проецирующей плоскостью α
Влевой половине листа (формат А3) в соответствии с вариантом за-
дания (табл. 3, рис. 8, 9) в масштабе 1:1 начертить две ортогональные про-
екции заданной пирамиды. Построить профильную проекцию пирамиды и след-проекцию α2 проецирующей секущей плоскости α. Фронтальная про-
екция линии сечения совпадет со следом-проекцией α2 секущей плоскости
α (в силу собирательного свойства этой проекции). Недостающие проек-
ции линии сечения строятся исходя из условия принадлежности точек этой линии заданной геометрической поверхности: точка принадлежит поверх-
ности, если лежит на какой-либо линии, принадлежащей этой поверхности.
Для пирамиды – это точки, принадлежащие ее ребрам (точки пересечения ребер пирамиды плоскостью α). Сначала определяются фронтальные про-
екции этих точек (12 , 22 , 32 , … на рис. 10 и 11) на линии α2, а затем стро-
ятся горизонтальные и профильные проекции этих точек. |
|
|
|
|||
Найденные |
точки |
соединяются |
отрезками |
прямых |
с |
учетом |
видимости. |
|
|
|
|
|
|

16
|
|
|
|
|
Таблица 3 |
|
|
|
|
|
|
|
|
Номер |
Заданная |
Числовые значения параметров |
||||
варианта |
фигура, рис. |
|
|
|
|
|
d, мм |
h, мм |
b, мм |
φ,° |
|||
|
|
|||||
1 |
9 |
72 |
78 |
45 |
45 |
|
2 |
8 |
70 |
80 |
44 |
50 |
|
|
|
|
|
|
|
|
3 |
9 |
74 |
72 |
47 |
40 |
|
4 |
8 |
78 |
78 |
46 |
35 |
|
|
|
|
|
|
|
|
5 |
9 |
70 |
74 |
43 |
35 |
|
6 |
8 |
72 |
76 |
46 |
40 |
|
7 |
9 |
82 |
82 |
50 |
45 |
|
8 |
8 |
74 |
78 |
47 |
45 |
|
9 |
9 |
74 |
76 |
45 |
35 |
|
|
|
|
|
|
|
|
10 |
8 |
76 |
82 |
46 |
50 |
|
11 |
9 |
78 |
76 |
48 |
45 |
|
|
|
|
|
|
|
|
12 |
8 |
80 |
74 |
48 |
30 |
|
13 |
9 |
80 |
76 |
46 |
45 |
|
14 |
8 |
82 |
80 |
50 |
45 |
|
15 |
9 |
76 |
76 |
44 |
50 |
|
16 |
8 |
70 |
68 |
42 |
35 |
|
|
|
|
|
|
|
|
17 |
9 |
78 |
72 |
45 |
30 |
|
18 |
8 |
72 |
70 |
47 |
40 |
|
|
|
|
|
|
|
|
19 |
9 |
78 |
76 |
44 |
45 |
|
20 |
8 |
76 |
80 |
48 |
50 |
|
21 |
9 |
76 |
70 |
45 |
30 |
|
|
|
|
|
|
|
|
22 |
8 |
84 |
80 |
52 |
40 |
|
23 |
9 |
74 |
74 |
44 |
35 |
|
|
|
|
|
|
|
|
24 |
8 |
76 |
74 |
48 |
30 |
|
25 |
9 |
72 |
76 |
46 |
40 |
|
26 |
8 |
76 |
74 |
48 |
45 |
|
27 |
9 |
80 |
78 |
40 |
40 |
|
28 |
8 |
82 |
80 |
50 |
45 |
|
|
|
|
|
|
|
|
17
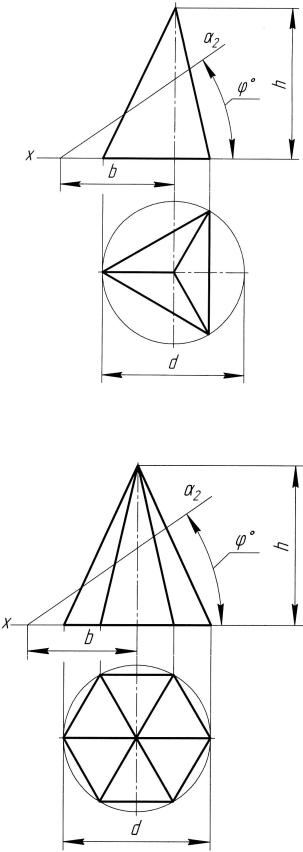
Рис. 8. Трехгранная пирамида
Рис. 9. Шестигранная пирамида
17
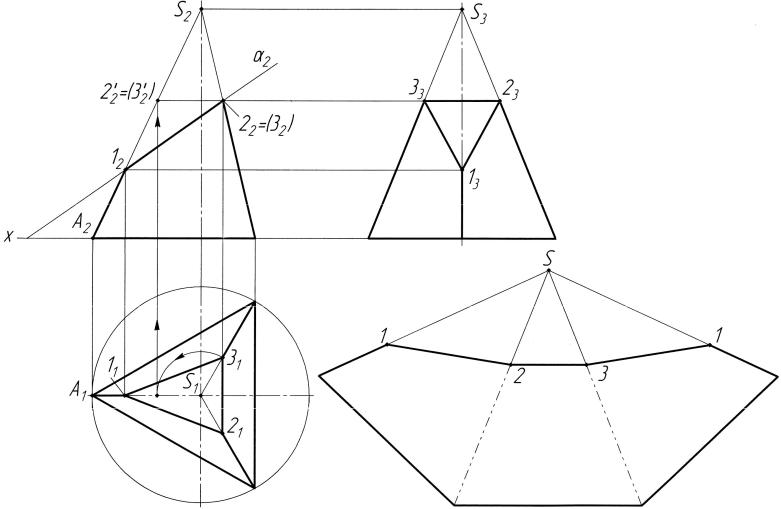
Рис. 10. Построение трех проекций и развертки боковой поверхности трехгранной пирамиды
18
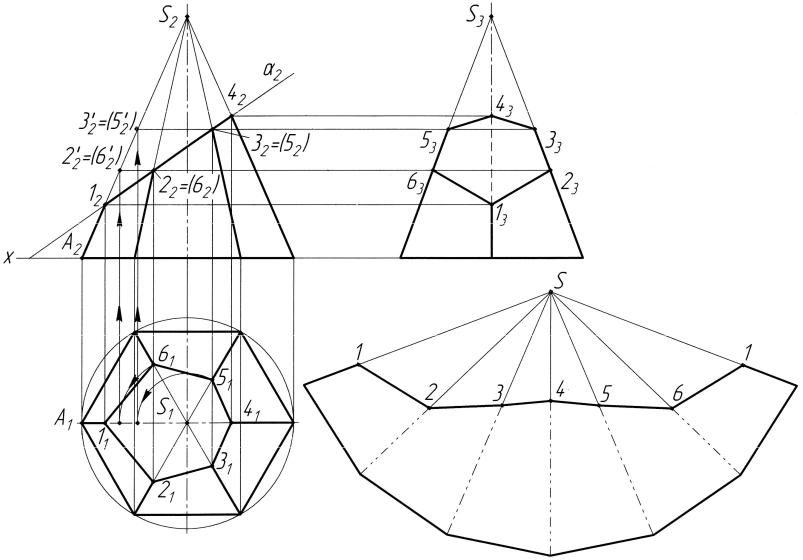
Рис. 11. Построение трех проекций и развертки боковой поверхности шестигранной пирамиды
20
Построение развертки боковой поверхности усеченной пирамиды
Развертка боковой поверхности пирамиды представляет собой пло-
скую фигуру, которая составлена из треугольников – граней пирамиды, со-
вмещенных с плоскостью (способ треугольников). При этом все грани на развертке изображаются в натуральную величину. Предварительно опре-
деляются натуральные величины всех ребер и сторон основания любым из известных способов. Развертка строится на свободном поле чертежа
(в правой половине листа).
На рис. 10 прямая трехгранная (на рис. 11 шестигранная) пирамида имеет в основании равносторонний треугольник(шестиугольник), распо-
ложенный горизонтально (׀׀ Π1). Поэтому на плоскость Π1 основание и,
следовательно, его стороны проецируются в натуральную величину. Ребра пирамиды равны между собой. Ребро SA ׀׀ Π2 – фронталь, поэтому на Π2
проецируется в натуральную величину. Каждая боковая грань на развертке строится как треугольник по трем сторонам, две из которых – это равные между собой боковые ребра, третья – сторона основания.
Для нанесения на развертку точек линии сечения нужно определить истинные расстояния этих точек от вершиныS, которые измеряются на
ребре SA.
На рис. 10 и 11 натуральные величины этих расстояний (S222', S232',
S252' и S262') определены методом вращения вокруг горизонтально-
проецирующей прямой, проходящей через вершину S пирамиды до поло-
жения, параллельного фронтальной плоскости проекций. Натуральные ве-
личины отрезков можно определить и любым другим известным способом
(замена плоскостей проекций, метод прямоугольного треугольника). Затем построенные точки следует соединить отрезками прямых линии.
