
Задача №4 ЭиЭ(1)
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Вятский государственный университет»
Факультет автоматики и вычислительной техники
Кафедра автоматики и телемеханики
Электротехника и электроника
Задача №4. «Схемные функции линейных электрических цепей»
Вариант №10
Студент: гр. УТ – 21 Петухов П.А.
Преподаватель: Ланских А.М.
Киров 2013
Задача:
-
Найти схемные функции
 ,
,
 ,
,
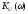 ,
,
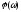 ,
,
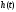 для данной схемы, соответствующей
заданному варианту.
для данной схемы, соответствующей
заданному варианту. -
Представить временную диаграмму работы схемы, если на её вход поступает последовательность прямоугольных импульсов с амплитудой
 ,
периодом
,
периодом
 и скважностью
и скважностью
 .
.
Схема и условия задачи:
Дано: R1=33
кОм, R2=13
кОм,
C1=0.02 мкФ, C2=0.1 мкФ,
T=10 мкс, Um=10 В,q=2;
Найти:
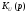 ,
,
 ,
,
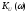 ,
,
 ,
,
 -?
-?
-
Найдём
 и
и
 :
:
Для получения схемных функций в операторном виде необходимо перенести схему и сигналы в плоскость изображений по Лапласу. Соответственно после проведения преобразования для данной схемы R1=R1, R2=R2, C1=1/pC1, C2=1/pC2.
Кроме того, представим параллельные элементы схемы в более удобном виде:


Преобразованная
схема будет выглядеть следующим образом:
Тогда Uвых=Z2(p)*I(p), а I(p)= Uвх(p)/(Z1(p)+ Z2(p)).
Заменим
Z1(p)
и Z2(p):


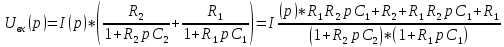
Коэффициент
передачи
 - это отношение изображения Лапласа
выходного сигнала цепи
- это отношение изображения Лапласа
выходного сигнала цепи
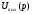 к изображению Лапласа входного сигнала
к изображению Лапласа входного сигнала
 при нулевых начальных условиях:
при нулевых начальных условиях:

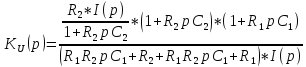

Комплексный
коэффициент передачи
 - амплитудно-фазочастотная характеристика
получается из передаточной функции
- амплитудно-фазочастотная характеристика
получается из передаточной функции
 путем замены переменной
путем замены переменной
 ,
т.е.
,
т.е.

2.Найдём
 :
:
Представим:

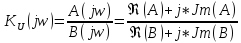
Тогда

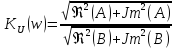
Re(A)=R2 , Re(B)=R2+R1, Jm(A)=wR1R2C1, Jm(B)=wR1R2(C1+C2).


Подставим данные значения R и C:

 - модуль комплексного
коэффициента передачи, являющийся
амплитудно-частотной характеристикой
(АЧХ) схемы. При
построении ЛАЧХ по оси ординат
откладывается
- модуль комплексного
коэффициента передачи, являющийся
амплитудно-частотной характеристикой
(АЧХ) схемы. При
построении ЛАЧХ по оси ординат
откладывается
 в логарифмическом масштабе, то есть
в логарифмическом масштабе, то есть
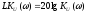 .
За единицу масштаба принимается децибел
(дБ), значение любого числа N,
выраженное в децибелах, равно
.
За единицу масштаба принимается децибел
(дБ), значение любого числа N,
выраженное в децибелах, равно
 .
По оси абсцисс откладывается частота,
за единицу масштаба которой выбирается
либо октава (для двукратного изменения
частоты), либо декада (для десятикратного
изменения частоты).
.
По оси абсцисс откладывается частота,
за единицу масштаба которой выбирается
либо октава (для двукратного изменения
частоты), либо декада (для десятикратного
изменения частоты).
Построим ЛАЧХ.
|
w,Гц |
0 |
1 |
10 |
50 |
100 |
200 |
500 |
1000 |
2000 |
3000 |
8000 |
10000 |
|
LKU,дБ |
-10.96 |
-10.96 |
-10.96 |
-10.97 |
-11 |
-11.1 |
-11.7 |
-12.9 |
-14.36 |
-14.92 |
-15.43 |
-15.47 |

3.Найдём φ(w):

Выражения для Jm и Re были найденны выше, подставим их:

Подставим данные значения R и C:

Построим ФЧХ.
|
w,Гц |
0 |
1 |
10 |
50 |
100 |
200 |
500 |
1250 |
2000 |
3000 |
8000 |
10000 |
|
φ(w) |
0 |
-0.026 |
-0.264 |
-1.315 |
-2.614 |
-5.106 |
-10.99 |
-14.94 |
-13.1 |
-10.22 |
-4.36 |
-3.5 |
w,Гц

4.Найдём выражение для h(t).
Переходная
функция (характеристика)
 представляет собой реакцию (выходной
сигнал) схемы на входное ступенчатое
воздействие
представляет собой реакцию (выходной
сигнал) схемы на входное ступенчатое
воздействие
 и численно
и численно
 .
При этом
.
При этом
 отличается от
отличается от
 только размерностью, поскольку
только размерностью, поскольку
 - безразмерная функция. Изображение
переходной функции
- безразмерная функция. Изображение
переходной функции
 и с учетом того, что
и с учетом того, что
 имеет своим изображением
имеет своим изображением
 ,
,
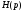 определяется как
определяется как
 .
.
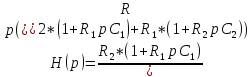
Если
 ,
то есть в знаменателе есть один нулевой
корень, то используется вторая формула
Хевисайда:
,
то есть в знаменателе есть один нулевой
корень, то используется вторая формула
Хевисайда:
 ,
,
где
 - корни многочлена
- корни многочлена
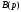 ;
;
 - вычисляется при
- вычисляется при
 ;
;
 ;
;
 - значение числителя
- значение числителя
 при
при
 ;
;
 - значение первой производной знаменателя
по переменной
- значение первой производной знаменателя
по переменной
 при
при
 .
.
 подставим вместо R
числовые значения:
подставим вместо R
числовые значения:
 .
.
Рассчитаем
p1:

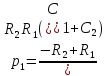 ,
подставим p1
и найдём C1:
,
подставим p1
и найдём C1:

После того, как найдены выражения для p1 и C1, подставим числовые значения и рассчитаем коэффициенты:


Итоговая
формула:

5. Построим временную диаграмму работы схемы.
Определим форму выходного сигнала с помощью интеграла Дюамеля:
 .
.

Зная,
что q=2,
T=10
мкс, найдём tu,
по формуле
 .
tu=5
мкс.
.
tu=5
мкс.
Подставим числовые данные :

Построим график выходного сигнала:
|
Uвых(t),В |
2.83 |
2.83 |
2.83 |
2.83 |
2.83 |
2.83 |
0.005 |
0.005 |
0.005 |
0.005 |
0.005 |
0.005 |
|
t,мкс |
0 |
1 |
2 |
3 |
4 |
5 |
5 |
6 |
7 |
8 |
9 |
10 |

Библиографический список: А.М. Ланских «Частотные и временные характеристики пассивных линейных четырёхполюсников»
Подпись студента _________________
Дата выполнения 19.11.2013
