
- •Решение задач оптимизации
- •2013 Г. Введение
- •Нахождение стационарной точки
- •Рис 1. Линии уровня функции и стационарная точка
- •2.Нахождение безусловного экстремума методами прямого поиска.
- •2.1.Метод поиска по симплексу
- •Рис 2. Графическое пояснение метода равномерного симплекса
- •2.2 Метод поиска Хука-Дживса
- •Рис 3. Графическое пояснение метода Хука-Дживса
- •2.3Метод сопряженных направлений Пауэлла
- •Рис 4. Графическое пояснение метода сопряженных направлений Пауэлла
- •3.Нахождение безусловного экстремума градиентными методами
- •3.1 Метод Коши
- •Рис 5. Графическое пояснение метода Коши
- •Рис 6. Графическое пояснение метода Ньютона
- •Метод сопряженных градиентов
- •Рис 7. Графическое пояснение метода сопряженных градиентов
- •Рис 8. Графическое пояснение квазиньютоновского метода Заключение
Рис 7. Графическое пояснение метода сопряженных градиентов
Квазиньютоновский метод
Описание алгоритма:
Данный метод обладает положительными чертами метода Ньютона, однако, использует информацию только о первых производных. В этом методе приближение к очередной точке в пространстве оптимизируемых параметров задается формулой:

Направление поиска определяется выражением:
 ,
где
,
где
 - матрица порядка
- матрица порядка (метрика).
(метрика).
Матрица
 - вычисляется по формуле.
- вычисляется по формуле.
 ,
где:
,
где:
 (1)
(1)
Где
 изменение градиента на предыдущем шаге.
изменение градиента на предыдущем шаге.
Данный алгоритм отличается устойчивостью, так как обеспечивает убывание целевой функции от итерации к итерации.
Алгоритм метода:
Шаг 1. Задать: начальную точку х(0). Перейти к шагу 2.
Шаг 2. Вычислить направление поиска s(k). Перейти к шагу 3.
Шаг
3. Произвести поиск вдоль прямой
 .
Перейти
.
Перейти
к шагу 4.
Шаг 4. Проверка условия окончания поиска.
Да: закончить поиск;
Нет: перейти к шагу 2.
Ход решения:
Исходные данные:
 -
целевая функция;
-
целевая функция;
Шаг 1.
 - начальная точка;
- начальная точка;

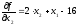
Шаг 2.


Положим

Шаг 3.
Поиск вдоль прямой:



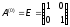
х(0) = [2,1176; 5,4836]T - [-10;-10]T = [12,1176; 15,4836]T;
g(0) = g(1) – g(0) = [3,7188; -2,9152]T - [-36;-46]T = [39.7188;43.085]T;





Шаг 4:
Поиск вдоль прямой:
х(2) =x(1)+(1)s(1)=[2,1176; 5,4836]T+(1)[-3,462; 3,194]T;
(1)=0,997;
x(2) = [-1,333;8.667]Т;
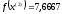
Точность метода позволяет уже на четвертом шаге считать текущую точку точкой-экстремумом. Т.е. х* = х(2) = [-1.333; 8,667]Т; f(x*) =7,6667.
Вывод: Квазиньютоновский метод позволяет достаточно быстро вычислить точку оптимума, и использует информацию только о первых производных в отличие от метода Ньютона. Неточность появляется вследствие округления.

Рис 8. Графическое пояснение квазиньютоновского метода Заключение
Анализируя результаты исследования (сравнения) всех рассмотренных выше методов, можно прийти к выводу о том, что каждый из них имеет свои достоинства и недостатки и более применим для задач одних видов и менее – для других. Однако, пользователь всегда сможет найти подходящий алгоритм для решения своей конкретной проблемы, выбирая как из вышеприведенного множества методов, так и из огромного спектра их модифицированных, усовершенствованных и комбинированных вариантов.
Однако, есть целый класс проблем, где найти оптимум либо крайне сложно, либо вообще невозможно получить точное решение с помощью алгоритмов данных категорий. К таким задачам относится, например, моделирование глобальных социально-экономических процессов.
Мощным инструментом теоретического исследования алгоритмов являются теоремы о сходимости методов. Однако, как правило, формулировки таких теорем абстрактны, при их доказательстве используется аппарат современного функционального анализа. Кроме того, зачастую непросто установить связь полученных математических результатов с практикой вычислений. Дело в том, что условия теорем труднопроверяемы в конкретных задачах, сам факт сходимости мало что дает, а оценки скорости сходимости неточны и неэффективны. При реализации алгоритмов также возникает много дополнительных обстоятельств, строгий учет которых невозможен (ошибки округления, приближенное решение различных вспомогательных задач и т.д.) и которые могут сильно повлиять на ход процесса.
Поэтому на практике часто сравнение алгоритмов проводят с помощью вычислительных экспериментов при решении так называемых специальных тестовых задач. Эти задачи могут быть как с малым, так и с большим числом переменных, иметь различный вид нелинейности. Они могут быть составлены специально и возникать из практических приложений, например задача минимизации суммы квадратов, решение систем нелинейных уравнений и т.п.
Приложение 1
Библиографический список.
Микрюкова В.И. «Методы оптимизации». – Киров, 2004.
Интернет.
