1.3.5. Правила построения примитивных кодов бчх

Коды Боуза-Чоудхури-Хоквингема (БЧХ) - это линейные блочные коды. При определенном построении они могут быть систематическими. Коды БЧХ представляют собой обобщенные коды Хэмминга, позволяющие исправлять кратные ошибки. В общем случае коды БЧХ являются циклическими. Коды БЧХ представляют большой класс легко строящихся кодов с варьируемыми в широких пределах длиной блока и скоростью. Достоинства этих кодов обусловлены не только гибкостью выбора их параметров, но и тем, что при длинах блока около нескольких сотен элементов многие из них являются оптимальными среди всех известных кодов с теми же длиной и скоростью.

О спектре кодов БЧХ в общем случае известно немного. В некоторых случаях, когда илимало, перебор позволяет найти спектр некоторых из этих кодов.

Примитивным кодом БЧХ, исправляющим ошибок, называется блоковый код длинойнад полем, для которого элементы(для произвольного) являются корнями порождающего многочлена, где - примитивный элемент поля .

Порождающий многочлен есть наименьшее общее кратное минимальных функций своих корней:

,

(1.22)

где - набор минимальных функций корней .

Коды с начальным значением называются кодами БЧХ в узком смысле.

Минимальные функции корней могут быть непосредственно вычислены по правилам, изложенным в п. 4.1.4, или найдены в табл.1.6 неприводимых многочленов.

Пример. Пусть нужно найти порождающий многочлен примитивного кода БЧХ (в узком смысле), исправляющего 3 ошибки и имеющего длину 15. Для этого корнями порождающего полинома должны быть элементы, ², ³, ⁴, ⁵, ⁶, где  - примитивный элемент поля GF(16) (количество корней определяется как ). Пусть полепорождается примитивным многочленом 23 (10011). Ниже приводится поле Галуа, в котором каждому элементу поля соответствует минимальная функция.

Вычисление минимальных функций корней дает

,

аналогично для других минимальных функций:

.

После перемножения полученных минимальных функций порождающий многочлен примет вид

.

Результирующий многочлен порождает (15,5)-код БЧХ, исправляющий три ошибки. Используя порождающий многочлен кода БЧХ можно получить проверочный многочлен, порождающую и проверочную матрицы. Кодирование и вычисление синдромов может быть осуществлено как по порождающему многочлену, так и по порождающей и проверочной матрицам.

Таблица 1.6

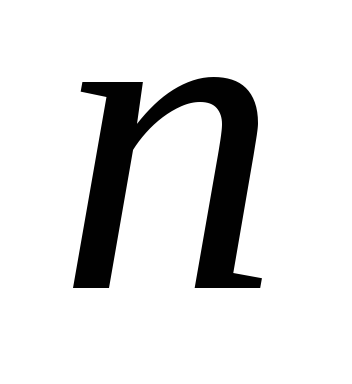
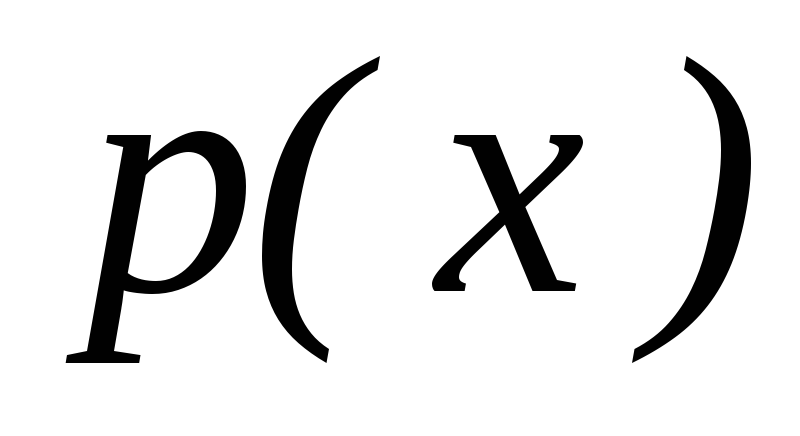
7	13
	15
15	023
	037
	007
	031
31	045
	075
	067
	057
	073
	051
63	103
	127
	147
	111
	015
	155
	133
	165
	007
	163
	013
	141

Примечание: все сомножители представлены в восьмеричной форме.