1.2. Коды, обнаруживающие ошибки

1.2.1. Двоичный безызбыточный код

Вся совокупность передаваемых сообщений может быть представлена в виде совокупности различных чисел. В этом случае имеет место числовой код. Максимальное количество возможных кодовых комбинаций в числовом коде .

Из всех числовых кодов наибольшее распространение получили двоичные коды. Причиной тому является простая арифметика двоичных чисел и возможность использования простых, дешевых и надежных в эксплуатации двухпозиционных элементов. Максимальное число возможных кодовых комбинаций в двоичном коде .

В безызбыточном двоичном коде все кодовые комбинации рабочие. Следовательно, , т.е. любая даже однократная ошибка приводит к ложному переходу одной рабочей кодовой комбинации в другую, и коэффициент ложных переходовдля любого(от 1 до).

Таким образом, безызбыточный двоичный код является непомехозащищенным кодом. Единственная защита такого кода от ошибок - фиксация нарушения количества элементов в кодовой комбинации. Поэтому, как правило, используется равномерный двоичный безызбыточный код.

1.2.2. Код с защитой по паритету (четности, нечетности)

Для придания двоичному коду свойства помехозащищенности, т.е. свойства обнаружения ошибок, в кодовые комбинации необходимо вводить дополнительные (избыточные, защитные, проверочные) разряды.

В двоичном коде с защитой по четности в кодовые комбинации вводится один защитный разряд, содержимое которого (0 или 1) дополняет число единиц в основных (информационных) разрядах до четности. При приеме сообщения бракуются (т.е. признаются ложными) все комбинации, содержащие нечетное число единиц.

Пример. В табл.1.3 приведены все рабочие кодовые комбинации двоичного кода с защитой по четности при числе информационных разрядов .

Таблица1.3

	Безызбыточный двоичный код	Двоичный код с защитой по четности
	000	000 0
	001	001 1
	010	010 1
	011	011 0
	100	100 1
	101	101 0
	110	110 0
	111	111 1

Данный код позволяет обнаружить все ошибки нечетной кратности.

1.2.3. Код с простым повторением

Число разрядов кода увеличивается в два раза по сравнению с безызбыточным кодом. Содержимое защитных разрядов повторяет содержимое информационных (рабочих) разрядов. Ошибки обнаруживаются путем сравнения содержимого информационных и проверочных разрядов. Число разрядов кода , где- проверочные разряды.

Пример. Рабочие комбинации кода с простым повторением (табл.1.4).

Таблица 1.4

	Код с повторением
	000 000
	001 001
	010 010
	011 011
	100 100
	101 101
	110 110
	111 111

Код позволяет обнаружить все ошибки нечетной кратности и значительную часть ошибок четной кратности.

1.2.4. Код с повторением и инверсией

Как и в коде с простым повторением, число проверочных разрядов равно числу информационных разрядов, т.е. . Однако содержимое проверочных разрядов совпадает с содержимым информационных разрядов лишь в случае четного числа единиц в информационных разрядах. При нечетном числе единиц в информационных разрядах содержимое проверочных разрядов представляет собой инверсию содержимого информационных разрядов.

Пример построения кода с повторением и инверсией приведен в табл.1.5.

Таблица 1.5

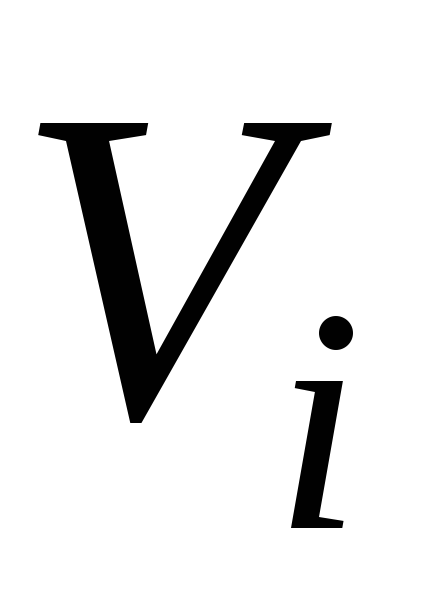
	Код с повторением
	000 000
	001 110
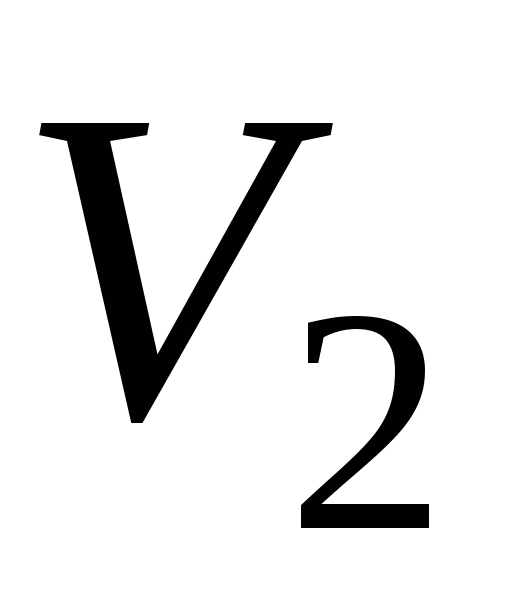
	010 101
	011 011
	100 011
	101 101
	110 110
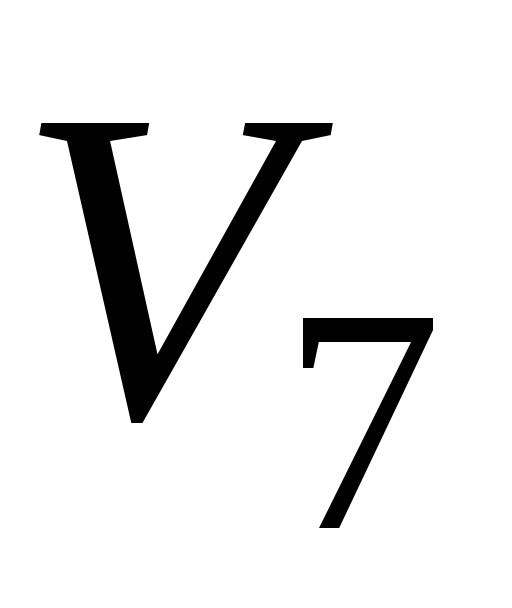
	111 000

Рассматриваемый код по сравнению с кодом с простым повторением является более помехоустойчивым, так как его минимальное кодовое расстояние больше. В рассмотренном примере .